




  |
 |  |  |
| Kapitel 06 Welt der Funktionen |
| Das Buch "Mathematik sehen und verstehen" wird erfreulicherweise etwa 2019 in der dritten Auflage erscheinen. Diese wird um etwa 20 Seiten umfangreicher sein. Sie befinden sich auf der Website zum Buch: Hier sind die Dateien aus GeoGebra und anderen Mathematik-Programmen, die die Bilder des Buches erzeugt haben. So können Sie alles interaktiv nachvollziehen. Die Vorlesung "Mathematik für alle" ist hier verfügbar. Weiter gibt es Ergänzungen, für die im Buch kein Platz mehr war. Insbesondere sind auch Aufgaben eingefügt. Bei Werkzeuge finden Sie ein Log-Buch und allerlei Hinweise. Falls nach dem Lesen im Buch noch Fragen übrig sind oder Sie Fehler finden, wenden Sie sich gern an mich. |
| Vorlesungen + Lectures in |
5 | 6 | 7 | 8 | 9 |
| 6.1 Familien | 6.2 Bauhof | 6.3 Ableitung | 6.4 Integral | 6.5 Hauptsatz. | 6.6 Höhere Dim, | ||||||||||||||||||||||
|
|
|
|
|
|
6.1 Funktionenfamilien |
||||

 Interaktive GeoGebra-Datei zur Stetigkeit Interaktive GeoGebra-Datei zur Stetigkeit |
||||
6.1.1 Parabeln und elementare Variationen |
||||||
| 6.1 Funktionenfamilien 6.1.1 Parabeln und elementare Variationen Abb.6.4 Abb.6.5 Verschieben |
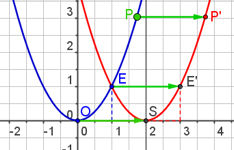  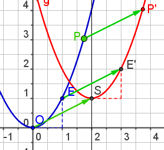
| Abb.6.5 Dies ist eine universale Datei zum Verschieben von Funktionen. Mit Variation von a schriebt man rechts-links, mit b hoch-runter. Die zu verschiebende Funktion kann durch "Umdefinieren" auch eine beliebige andere sein. | ||||
| Abb.6.6 | 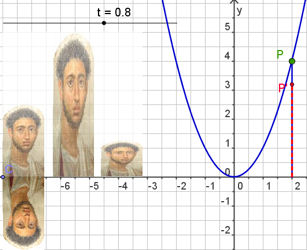
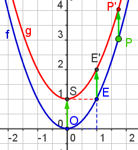
| Abb.6.6 Auch hier kann man die Funktion beliebig umdefinieren. Falls die Spur von P stört, kann man sie wegwischen oder abschalten (siehe Werkzeugseite). | ||||
| Abb.6.7 | 
| Abb.6.7 Hier kann man leicht das Bild austauschen und ein eigenes digitales Foto verwenden. | ||||
| Ergänzung | 
| |||||
| Aufgabe 6.1 | 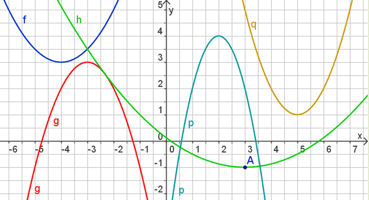 | |||||
6.1.2 Geraden und Potenzfunktionen |
||||||
| 6.1 Funktionenfamilien 6.1.2 Geraden und PotenzfunktionenAbb. 6.9 |
| Abb.6.9 | ||||
| Abb.6.10 Aufgabe 6.2 Lösung Kap. 13 und hier |
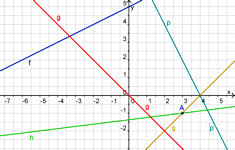
| Abb.6.10 | ||||
| 6.1 Funktionenfamilien 6.1.2 Geraden und Potenzfunktionen Abb.6.11 |
| Abb.6.11 | ||||
| Abb.6.12 | 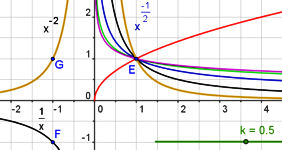
| Abb.6.12 | ||||
| Abb.6.13 Aufgabe 6.3 Lösung Seite 319 |
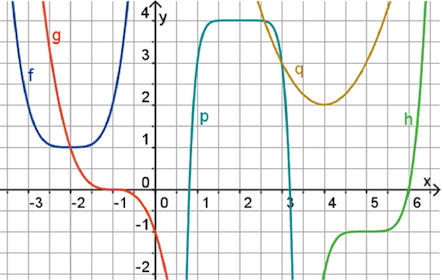
| Abb.6.13 | ||||
| Abb. neu | 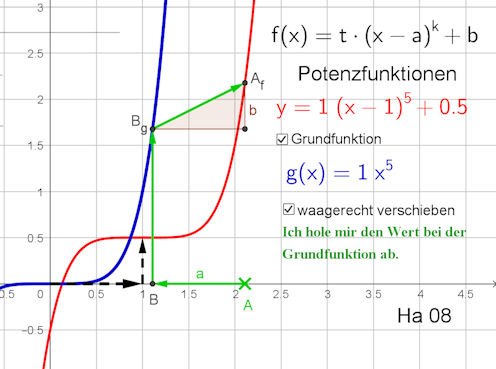
| |||||
| ||||||
6.1.3 Polynome in ihrer Vielfalt |
||||||
| 6.1 Funktionenfamilien 6.1.3 Polynome in ihrer Vielfalt Abb.6.14 Seite 133 Abb. 6.15 |
| Abb.6.14 Variieren Sie zunächst die Nullstellen, z.B. schieben Sie den Regler von c nach rechts. Beobachten Sie, wie sich stets der ganze Graph verändern muss. Mit dem Streckfaktor k können Sie den Graphen zurück in das sichtbar Fenster holen. Auf Seite 132 wird dann die Vielfachheit der Nullstellen erklärt. Sie können sie mit r, s und t verändern. Auch auf jede solche Änderung muss der gesamte Graph reagieren. | ||||
| Aufgabe 6.4 Aufgabe 6.5 Abb.6.17 Abb.6.18 Lösungen Kap 13 Abb.13.9- Abb.13.11 |
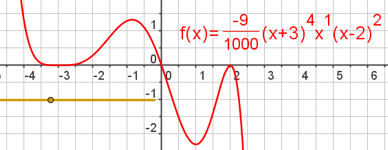
| 6.17 Die Beispiele mit drei Nullstellen können Sie auch mit der obigen Datei erkunden. Mit der folgenden Datei stelle ich Ihnen aber auch noch extra eine Spielwiese zur Verfügung. Klicken Sie doppelt auf den Term von f und tragen Sie ein, was Sie möchten. Mit dem Streckfaktor t können Sie den Graphen zurück in das sichtbar Fenster holen. | ||||
| Polynome Abb. 6.14 Abb. 6.16 |
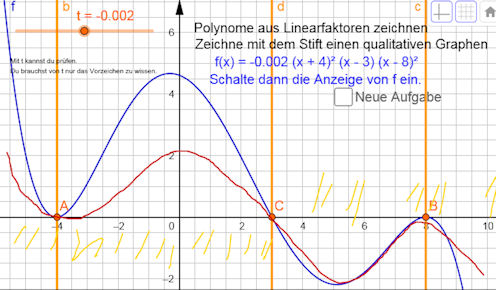
| Abb.6.16 | ||||
| Abb.6.18 | 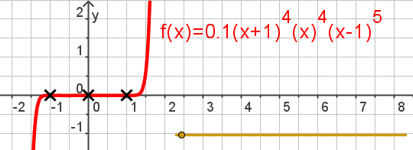 | Abb.6.18 | ||||
| Abb.6.19 | 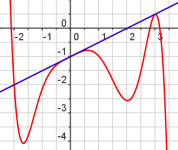 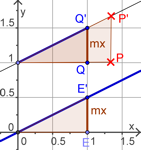
| Abb.6.19 Mehr zur Scherung folgt im Abschnitt zu Affenkästen. Hier einer Ergänzung dazu: Eine Scherung ist eine Abbildung, bei der es eine Scherachse gibt und einen Scherwinkel. Alle Punkte P wandern parallel zur Scherachse so, dass das Lot von P auf die Scherachse um den Scherwinkel kippt. Mehr zur Scherung folgt im Abschnitt zu Affenkästen. Hier einer Ergänzung dazu: Eine Scherung ist eine Abbildung, bei der es eine Scherachse gibt und einen Scherwinkel. Alle Punkte P wandern parallel zur Scherachse so, dass das Lot von P auf die Scherachse um den Scherwinkel kippt.Im Zusammenhang mit Funktionen entsteht durch Addition einer Geraden zum Funktionsterm eine Scherung. Bei festem b ist die Scherachse die y-Achse und der Scherwinkel ist der Steigungswinkel der Geraden. So ist es in obiger Datei verwirklicht. (Mit Betrachtung von b ist die Scherachse eine Parallele zur y-Achse durch die Nullstelle der Scher-Geraden.) Ausblick: Scherungen sind flächentreu. In dem Bild sind die Flächen zwischen dem Funktionsgrapen und der Geraden in jeder Stellung der Geraden genau gleich groß. | ||||
| In 6.1.3 Extra: Neu in der 3. Auflage Polynome im Affenkasten | ||||||
| 6.1 Funktionenfamilien 6.1.4 ff Polynome im Affenkasten Abb.6.20 |
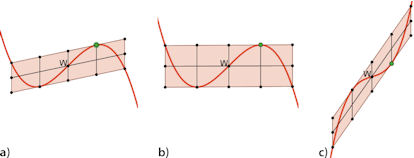
| Abb. 6.20 Jedes Polynom dritten Grades hat einen Wendepunkt W. Mit einem beliebigen anderen Punkt, hier grün dargestellt, definiert W einen Kasten aus acht gleichen Zellen, in dem das Polynom quasi "gefangen" ist. Sie sehen kein Koordinatensystem, weil das Gezeigte für jedes Polynom dritten Grades gilt. |
||||
| Abb.6.21 | 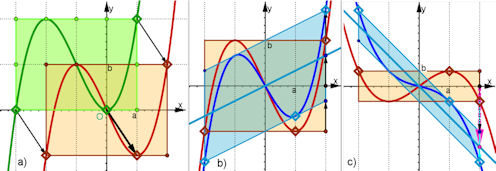 | Abb. 6.21 Zur Begründungskette für den Affenkasten. a) Start mit den drei dicken grünen
Punkten und dem zugehörigen Graphen. Die Kastenzellen haben die Abmessungen a und b. Verschiebung des Zentrums des Graphen in den Ursprung ergibt den
punktsymmetrischen rote Graphen.
b) Es folgt eine Scherung durch Addition einer Geraden y = mx mit m = 1/2, es ergibt sich der blaue Graph, die Kastenzellen sind nun Parallelogramme. Die Seite parallel zur y-Achse hat weiterhin die Länge b, dagegen ist a nun die (waagerechte) Höhe dieser Parallelogramme. Die Zellen haben daher ihren Flächeninhalt nicht geändert. c) Die Scherung wird durch Addition der Geraden y = - x bewirkt. Die schrägen Kastenkanten sind, wie bei b), nun Tangenten. |
||||
| 6.1 Funktionenfamilien Parabeln im Bärenkasten Abb.6.22 | 
| Abb. 6.22 Es gibt nur eine Parabel in der Welt,wenn man von Maßstab absieht. Sie sehen
vier Parabeln p(x) = a x(x - b). Diese repräsentieren eine allgemeine Parabel, denn bei jeder
beliebigen Parabel kann man einen Punkt in den Ursprung schieben. Dann hat ihre Gleichung
diese Gestalt. a) a = 1; b = 1, b) a = 5; b = 1, c) a =-8; b = 2018, d) a = 0.1; b = 100
In einem "goldenen" Rechteck mit dem Seitenverhältnis f : 1, siehe 11.1, sind die Bilder
gezeichnet und enthalten für das Intervall [-b; 2b] die Ordinaten vollständig.
|
||||
| Abb.6.23 | 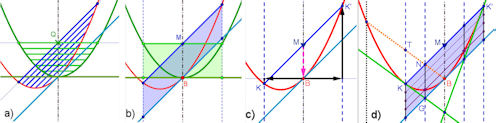
| Abb. 6.23 Parabel: Sehnen, Tangenten, Bärenkasten Begründungen folgen im Text des Buches. a) Zu einer Parabeltangente gehören parallele Parabelsehnen, deren Mitten auf einer Parallelen zur Parabelachse durch den Berührpunkt liegen. b) Zu jeder Parabelsehne gehört ein Bärenkasten, dessen gegenüber liegender Rand in seiner Mitte eine Tangente "trägt". c) Konstruktion einer Parabeltangente zu gegebenem Berührpunkt B auf einer Parabel (rot). d) Bei einem Bärenkasten mit Viertelteilung in beiden Richtungen, werden die beiden bei B liegenden Zellen in ihren inneren Ecken von der Parabel getroffen. Ihre äußeren Ecken erlauben das schnelle Zeichen von "Randtangenten2. Diese schneiden sich so, dass die Strecke vom Schnittpunkt nach M von Punkt B halbiert wird. Gepunktet sind Beweiselemente, die dann fehlen können. |
||||
| 6.1 Funktionenfamilien Polynome 4. Grades im Patherkäfig Abb.6.24 | 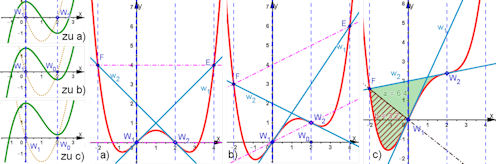
| Abb. 6.24 Polynome 4. Grades und ihr Pantherkäfig Begründungen folgen im Text des Buches. In der vorderen Spalte sind die ersten und zweiten Ableitungen der in a), b) und c) dargestellten (roten) Polynome 4. Grades zu sehen. Für diese gibt es stets ein durch den Abstand der Wendestellen definiertes Raster aus vier blau gestrichelten Stangen, den Pantherkäfig. Auf seinen äußeren Stangen schneiden die beiden Wendetangenten das Polynom. a) Was man für diesen symmetrischen Fall, die W-Form, beweist, gilt dann auch für die gescherten Fälle. b) zeigt die durch Scherung verzogene W-Form mit drei Extrema, c) zeigt, dass bei nur einem Extremum und einem schrägen Sattel die besonderen Eigenschaften weiter gelten. Die hier gezeigte Halbierung der Fläche zwischen einer Wendetangente und dem Polynom gilt auch für a) und b). Der Name "Pantherkäfig" lehnt sich an das eindrucksvolle Gedicht von Rilke an, in dem von dem Panther im Käfig gesagt wird: "ihm ist, als ob es tausend Stäbe gäbe und hinter tausend Stäben keine Welt". Nun sind nämlich keine Kastenzellen, sondern senkrechte Parallelen wichtig. Die Relexion über den didaktischen Sinn von solchen Redeweisen erfolgt im Buch. |
||||
Ende der neuen Seiten: Polynome im Affenkasten  | ||||||
6.1.4 Sinus, Kosinus und Musik |
||||||
| 6.1 Funktionenfamilien 6.1.5 Sinus, Kosinus und Musik Abb.6.25 |
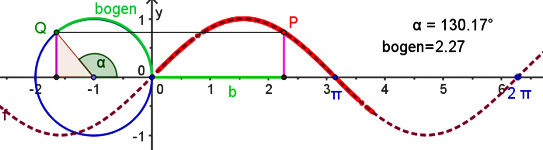 |
Abb.6.25 Beachten Sie, dass man an dieser Datei auch am besten den Zusammenhang zwischen "Bogenmaß" und "Winkelmaß in Grad" verstehen kann. Im Zusammenhang mit anderen Funktionen ist das Bogenmaß unerläßlich. Mit einer Beschriftung der Rechtsachse im Gradmaß könnte mit man die Funktionen f(x)=sin(x) nicht zusammen mit anderen Funktionen verwenden. Dieses vertieft Kapitel 6.2. | ||||
| Abb.6.26 | 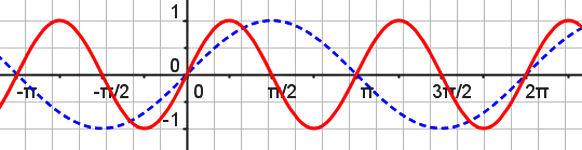
| Abb.6.26 | ||||
| Abb.6.26 | 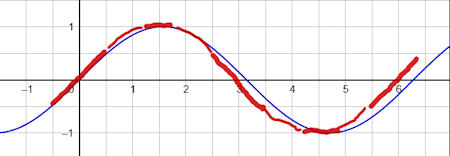
| Abb.6.26 | ||||
| Abb.6.27 | 
| Abb. 6.27 |
||||
| Abb.6.28 | 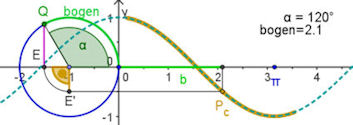
| Abb.6.28 | ||||
| Abb.6.29 | 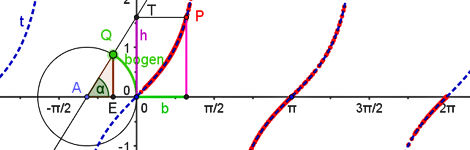
| Abb.6.29
| ||||
| Abb.6.29 | 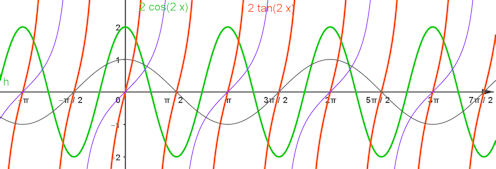 -->
-->
| Abb.6.29 | ||||
6.1.5 Exponentialfunktionen |
||||||
| 6.1 Funktionenfamilien 6.1.5 Exponentialfunktionen Abb.6.30 |
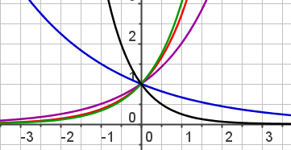
| Abb.6.30 | ||||
| Abb.6.31 | 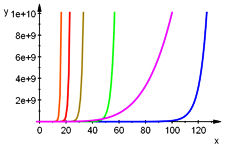 <
<
| Abb.6.31 | ||||
6.1.6 Umkehrfunktionen |
||||||
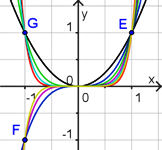
| 6.1 Funktionenfamilien 6.1.6 Umkehrfunktionen Abb.6.32 |
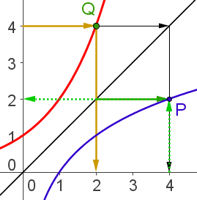
| 6.32 | ||||
| Abb.6.33 | 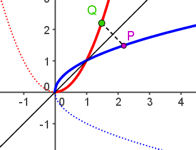
| Abb.6.33 | ||||
6.2 Funktionenbauhof |
||||||
| 6.2 Funktionenbauhof 6.2.1 Summe von Funktionen Abb.6.34 |
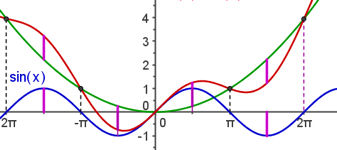
| Abb.6.34 | ||||
| 6.2 Funktionenbauhof 6.2.2 Produkt von Funktionen Abb.6.35 |
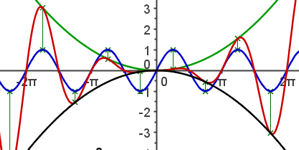
| Abb.6.35 | ||||
| 6.2 Funktionenbauhof 6.2.3 Verkettung von Funktionen Abb.6.36 |
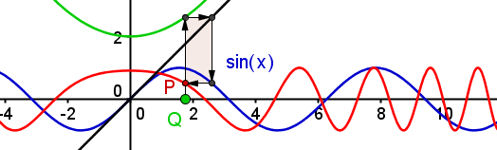
| Abb.6.36 \(f(x)=\sin{x^2}\) Die Funktionen können umdefiniert werden. Dann kann man mit dieser Datei alle Verkettungen visualisieren. | ||||
| Abb.6.39 |
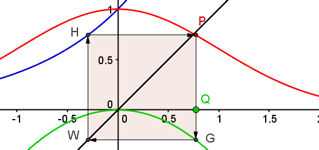
| Abb.6.39 \(f(x)=e^{-\frac{x^2}{2}}\)  | ||||
6.2.4 und 6.2.5 Kehrwert-Funktionen, Quotienten von Fkt |
||||||
Neu in der 3. Auflage: Kehrwert-Funktionen, Quotienten von Fkt., Quotienten von Polynomen | ||||||
| Funktionenbauhof 6.2.4 Kehrwert-Funktionen Abb.6.40 | 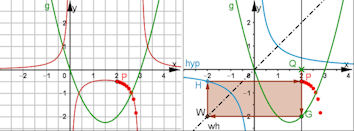
| Abb.6.40 | ||||
| Funktionenbauhof 6.2.5 Quotienten von Funktionen Abb.6.41 |
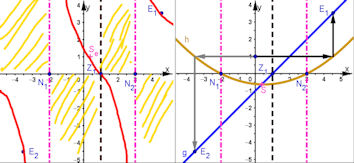
| Abb.6.41 | ||||
| Abb.6.42 | 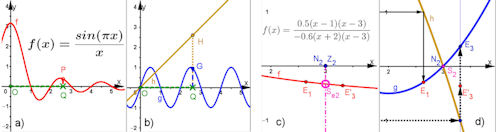
| Abb.6.42 | ||||
Neu in der 3. Auflage: 6.2.6 Quotienten von Polynomen |
||||||
| Funktionenbauhof 6.2.6 Quotienten von Polynomen Abb. 6.43 | 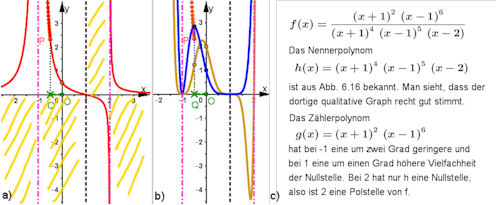
| Abb.6.43 | ||||
| Abb.6.44 | 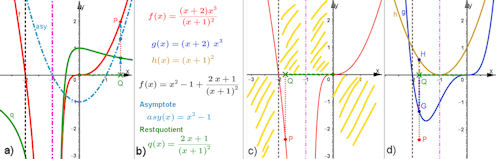
| Abb.6.44 | ||||
| Abb.6.45 | 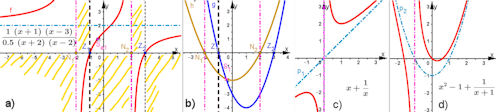
| Abb.6.45 | ||||
Ende der neuen Seiten zu Quotienten 
| ||||||
6.3 Blick auf den Punkt: Ableitung | ||||||
| ||||||
| 6.3 Blick auf den Punkt: Ableitung Abb.6.46/47 |
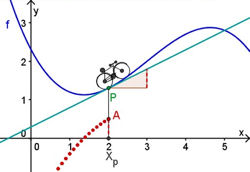
| Abb.6.46/47 | ||||
| 6.3 Blick auf den Punkt: Ableitung
6.3.1 Ableitungsfunktion vs. Sekantensteigungsfunktion Abb.6.48 |
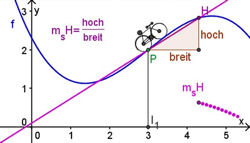
| Abb.6.48 Wichtiger Tipp: Bewegen Sie zunächst H mit den Pfeiltasten, dann verschwindet die Sekante, wenn H auf P fällt. Wenn Sie nämlich H mit der Maus ziehen, dann können Sie P nicht mehr exakt treffen, und es gibt scheinbar überall eine Sekante. Auch P dürfen Sie nur mit den Pfeiltasten bewegen, wenn Sie diesen didaktisch sinnvollen Effekt bewahren wollen. Falls Sie dennoch P oder H mit der Maus angefasst haben, können Sie rechts oben im Applet mit dem Doppelpfeil-Icon die ursprüngliche Version wieder herstellen. Die Tangente können Sie mit dem Schaltkästchen unter dem Bild anzeigen lassen. Die Ableitung können Sie mit der rechten Maustaste auf f3 links und "Objekt anzeigen" dazuschalten. | ||||
| 6.3 Blick auf den Punkt: Ableitung
6.3.1 Ableitungsfunktion Eigenschaften Abb.6.49 |
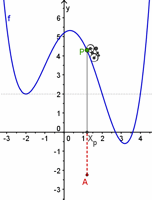 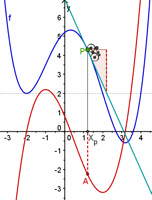
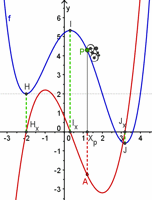 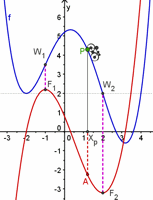
| Abb.6.49 Wenn Sie sich Kopien dieser Datei machen, können Sie sie für beliebige Beispiele nutzen. Die gesammte "Kurvendiskussion" ist dann auch gleich dabei. | ||||
| Abb.6.50 | 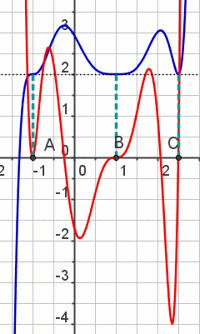
| Abb.6.50 Stellen Sie Sätze auf wie: Ein Sattel der Ordnung m bei der Funktion f erzwingt eine Berührnullstelle der Ordnung m-1 bei der Ableitung f'. Ein Extremum der Ordnung m........ Wie auch im Buch ist für f eine (variierbare) Höhenlage gewählt, damit sich die Phänomene optisch trennen. | ||||
| Abb.651 | 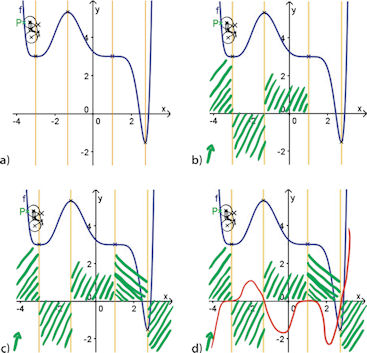 Qualitativer Ableitungsgraph, ereugt durch Felderabstreichen. Die Vorgehensweise ist im Buch als Ablauf ausführlich beschrieben. | |||||
Die e-Funktion, das Geheimnis wird gelüftet | ||||||
| 6.3.2 Hinführung zur e-Funktion Abb.6.52 Abb.6.53 |
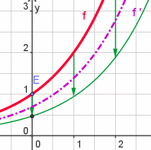
| 6.52 Die Erläuterung steht ausführlich im Buch Abschnitt 6.3.2. und auch in der Vorlesung 7. | ||||
6.4 Blick auf das Ganze: das Integral | ||||||
| ||||||
| Modellierung beim Wetter, Weg zum Integral | ||||||
| 6.4 Integral
Abb.6.54 |
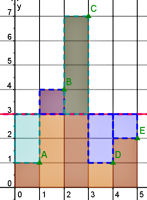
| Abb.6.54 | ||||
| Abb.6.56 | 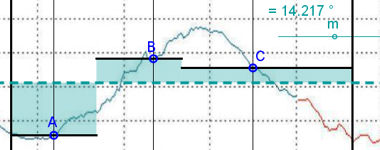 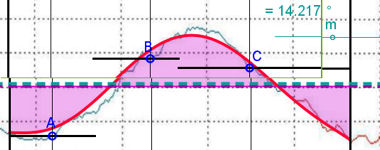
| Abb.6.56 | ||||
6.4.1 Definition des Integrals | ||||||
| 6.4 Integral 6.4.1 Definition des Integrals Abb.6.58 Abb.6.59 Abb.6.60 Ergänzung |
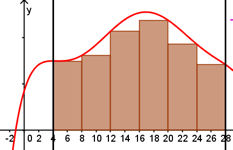
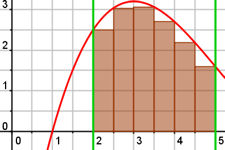
| Abb.6.58 In der universellen Datei können anstelle von f auch beliebige andere Funktionen eingetragen werden. | ||||
| Ergänzung Integral-Übung | 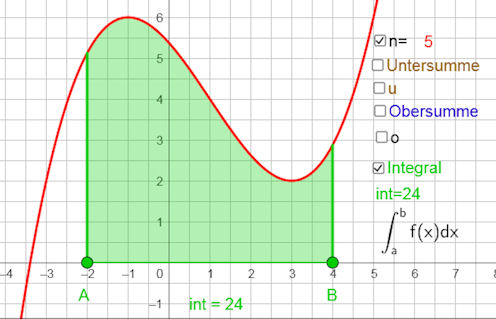
| Es ist hier sinnvoll, sich die Wirkung der Vertauschung der Grenzen klarzumachen. Flächen unter der x-Achse werden im Integral negativ gezählt. Das kann man hier auch beobachten. | ||||
6.4.2 Weitere Anwendungen des Integrals | ||||||
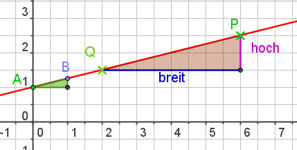
| Ergänzung Fläche zwischen Funktionsgraphen |
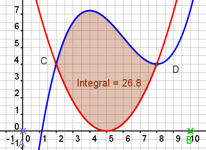
| |||||
| Mittelwert suchen |
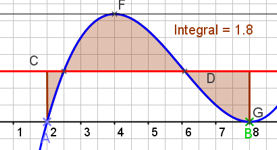
| |||||
6.5 Großartiger Zusammenhang: der Hauptsatz | ||||||
| 6.5 Hauptsatz der Differenzial- und Integralrechnung Abb.6.63 Abb.6.64 Abb.6.65 |
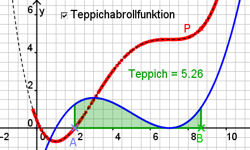
| Abb.6.63 | ||||
| Abb.6.66 | 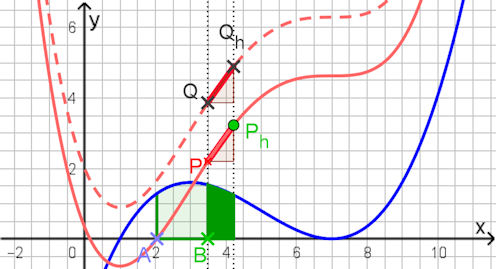
| Abb.6.66 | ||||
Weiteres zur Analysis ist im Buch und auf der Website
| ||||||
6.6 Funktionen in höheren Räumen | ||||||
| 6.6 Höhere Dimensionen |
||||||
|
||||||
| www.mathematik-sehen-und-verstehen.de URL: https://masuv.web.leuphana.de |