ISBN 978 662 69291 2 Auflage 2 Book Springer Spektrum
ISBN 978 662 69292 9 Auflage 2 eBook
www.mathematik-sehen-und-verstehen.de
https://masuv.web.leuphana.de (Sicherer Zugang)
Dieter Riebesehl
Hubert Dammer |
Höhere Mathematik sehen und verstehen
ISBN 978 662 69291 2 Auflage 2 Book Springer Spektrum ISBN 978 662 69292 9 Auflage 2 eBook www.mathematik-sehen-und-verstehen.de https://masuv.web.leuphana.de (Sicherer Zugang) |
Dörte Haftendorn Dieter Riebesehl Hubert Dammer |
|
| Kapitel 3 Analysis 3D |
|
||
 3.1 Funktionen |
||
| Abschnitt 3.1 Seite 248 1. Auflage: 3.1.1 Seite 224  |
|
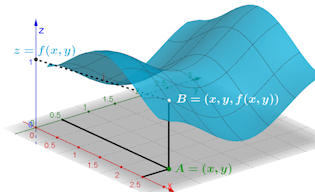
Abb. 3.1 Graph
einer Funktion von zwei Veränderlichen. Über jedem Punkt \(A\) in der
xy-Ebene wird der Punkt \(B\) mit \(z-\)Koordinate \(f(x,y)\) gezeichnet.
Die Gesamtheit dieser Punkte ergibt den Graphen der Funktion \(z=f(x,y)\).
Funktionsgraph3d.ggb 
|
| 3.2 Differentialrechnung 3D |
||
| Abschnitt 3.1 Seite 249 1. Auflage: 3.1.1.1 Seite 225 |
Dieses "Gebirge" wird im Rahmen des Lagrange-Verfahrens noch ausführlich untersucht. |
Abb. 3.2 Funktion zweier Veränderlicher
dargestellt mit Höhenlinien. Gezeigt ist von links nach rechts:
Schnitt des Graphen von \(f\) mit einer Ebene parallel zur xy-Ebene;
viele solche Schnitte in gleichen \(z-\)Abständen; das Gerüst der
Schnittkurven ohne den Graphen von \(f\); Blick auf dieses Gerüst
senkrecht von oben, so dass man die Schar der Höhenlinien in der
xy-Ebene sehen kann. Im letzten Bild sind noch die Koordinatenachsen
eingezeichnet. Gut erkennbar: der steilere Hügel erzeugt die
engeren Höhenlinien.
Hoehenlinien.ggb
|
| Abschnitt 3.3 Seite 251 1. Auflage: 3.2 Seite 227 |
|
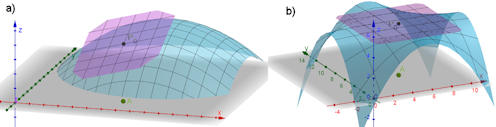
Abb. 3.3 Funktionen zweier Veränderlicher mit
Tangentialebenen in einem Punkt. a)
zeigt die allgemeine Situation, sie
wird im Folgenden mehrfach aufgegriffen. b) zeigt ein Beispiel,
bei dem in \(P_0\) in allen Richtungen
stetig differenzierbare Schnittkurven existieren,
die alle in \(P_0\) die Steigung 0 haben. Daher ist die
Tangentialebene horizontal.
Tangentenflaeche.ggb
Tangentenflaeche2.ggb
|
| Abschnitt 3.2.1 Seite 251 1. Auflage: Seite 227 |
|
Abb. 3.4 Partielle Ableitungen.
Die gezeigten Schnittkurven von \(f\) mit den
Ebenen \(y=y_0\) und \(x=x_0\) durch den Punkt
\(A = (x_0,y_0)\) sind stetig differenzierbare
Kurven (rot bzw. grün).
Die blauen Vektoren zeigen ihre Tangenten im Punkt \(B=P_0\).
partielle-ableitungen.ggb
partielle-ableitungen-pur.ggb
|
| Abschnitt 3.2.1.1 Seite 252 1. Auflage: Seite 228 |
|
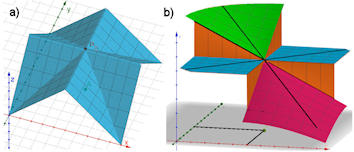
Abb. 3.5 Existenz von Tangentialebenen.
a) In \(P_0\) existieren die
partiellen Ableitungen, aber keine Tangentialebene. b) Im
zentralen Punkt sind alle Richtungsableitungen sogar stetig, aber es gibt
dennoch keine Tangentialebene. Weiteres steht im Text.
Tangentenflaeche-keine.ggb
Tangentenflaeche-keine-2.ggb
|
| Abschnitt 3.2.1.1 Seite 254 1. Auflage: Seite 230 |
|
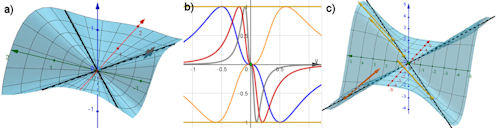
Abb. 3.6 Bilder zur Polardarstellung und zu speziellen Ableitungen.
a) Raumfläche in Polarkoordinaten mit den Geraden aus c) als
Regelfläche, siehe auch Abschnitt 2.7.8,
b) Graphen zu \({f}_y(x_0,y)\)
für \(x_0\in \{-0.5,\,-0.2,\,-0.1,\,0.6\},\) die extremale Steigung \(\pm 1\)
ergibt sich stets für \(y=\pm x\).
c) Raumfläche mit den Schnittgeraden der Ebenen, die auf den
Winkelhalbierenden von x- und y-Achse senkrecht stehen.
Auf Einzelheiten geht der Text ausführlich ein.
flaeche3.6-polar.ggb
flaeche3.6-kartesisch.ggb
|
| Abschnitt 3.2.1.2 Seite 255 1. Auflage: 3.2.1.1 Seite 231 |
|
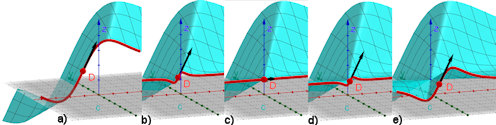
Abb. 3.7 Detailbilder
mit Schnitten parallel zur x-Achse a) - e): \(y\)
läuft von kleinen positiven zu kleinen negativen Werten und ist in
c) genau null.
Gegenbeispiel 2d-differenzierbar ySchnitt.ggb
|
| Abschnitt 3.2.1.2 Seite 256 1. Auflage: 3.2.1.1 Seite 232 |
|
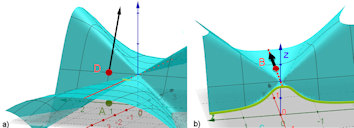
Abb. 3.8 Gegenbeispiel ohne
Tangentialebene trotz stetig differenzierbarer Schnittkurven.
a) Graph von
\(f\) mit einem Steigungsvektor,
b) Schnitt des Graphen mit einer Ebene parallel zur y-Achse
nahe am Ursprung.
Gegenbeispiel 2d-differenzierbar ySchnitt.ggb
Gegenbeispiel 2d-differenzierbar ySchnitt-links.ggb
|
| Abschnitt 3.2.2 Seite 257 1. Auflage: Seite 233 |
|
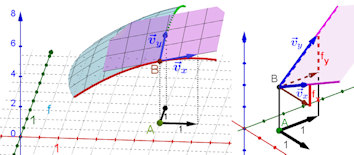
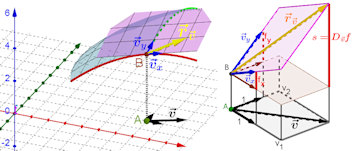
Abb. 3.9 Richtungsableitung zu
einem Vektor \(\vec v=(v_1,v_2)^{\rm T}\): Nach
Definition 3.2 gilt in \(B=P_0\):
\(f_x=f_x(x_0,y_0)\),
\(f_y=f_y(x_0,y_0)\);
\(s=v_1\cdot f_x+ v_2\cdot f_y\) gilt geometrisch, nach
Satz 3.2 ist dies die Richtungsableitung
\(D_{\vec v}f=\vec{\nabla}f \cdot \vec{v}\) in \(B\).
Tangentenflaeche-Richtungsableitung-g.ggb
Richtungsableitung-pur.ggb
|
| Abschnitt 3.2.2.1 Seite 259 1. Auflage: 3.2.2 Seite 235 |
|
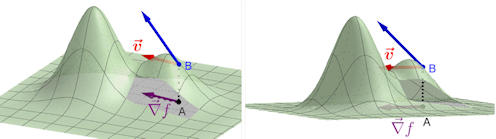
Abb. 3.10 Raumfläche mit wanderndem Gradienten. Links ist
durch das Fenster im
Graphen in der xy-Ebene liegend an \(A\) angehängt der Gradient \(\vec\nabla f\) (violett)
zu sehen; auf dem Graphen, senkrecht darüber, an den
Punkt \(B\) angehängt dann waagerecht der Richtungsvektor \(\vec v\) (rot) zur Richtungsableitung
und der Tangentialvektor (blau) der grünen Raumfläche.
Zufällig hat der Gradient die Länge 1, sodass man rechts mit dem
richtigen Blickwinkel erkennen kann, dass hier auch 1 die Steigung der
Tangente ist. Experimentieren Sie durch
beliebiges Ziehen an \(A\).
Wenn Sie sich vorstellen, Sie würden in \(B\) Wasser ausgießen,
so wird es genau entgegen der gezeigten Tangentenrichtung den
Berg hinunterfließen.
Gradient-Gebirge.ggb
Gradient-Gebirge2.ggb
|
| Abschnitt 3.2.2.2 Seite 259 1. Auflage: 3.2.2.1 Seite 235 |
|
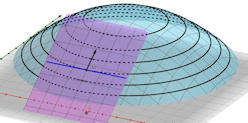
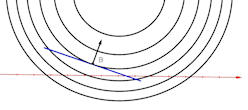
Abb. 3.11 Gradient im
Höhenlinienbild. Links ist eine Tangentialebene in einem Punkt \(B\)
einer Höhenlinie gezeigt. Die Tangente an die Höhenlinie in \(B\) liegt
auch in dieser Tangentialebene. Rechts ist das Höhenlinienbild mit der
Tangente an die Höhenlinie in \(B\) zu sehen. Man sieht: der Gradientenvektor steht
senkrecht auf der Tangente an die Höhenlinie im Punkt \(B\).
Tangentenflaeche-Hoehenlinie.ggb
|
| Abschnitt 3.2.2.2 Seite 261 1. Auflage: 3.2.2.1 Seite 237 |
|
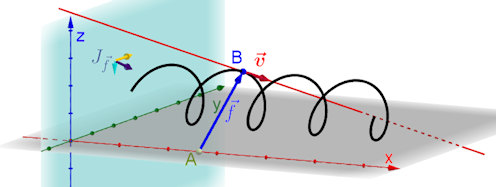
Abb. 3.12 Raumkurve mit Tangente. Der Graph von \(\vec f\)
ist eine Schraubenlinie. \(\vec v\) ist ein Tangentialvektor im Aufpunkt
\(B = \vec f(A),\ A=(x_0,0,0)\). Mit \(\lambda=x-x_0\) als Parameter hat
\(\vec v\) die Darstellung \((1,J_{\vec f})^{\rm T}\).
RaumkurveTangente.ggb
|
| Abschnitt 3.2.3 Seite 262 1. Auflage: Seite 238 |
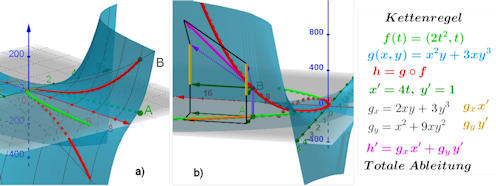
Sehen Sie sich diese Bilder aon allen Seiten an! |
Abb. 3.13 Kettenregel und totale Ableitung.
a) Die (grüne) Funktion \(f\) ist die Parameterdarstellung einer
Parabel mit dem Scheitel im Ursprung und der Öffnung in
Richtung der positiven x-Achse. Die (blaue) Raumfläche ist durch
\(g\) gegeben, und die Verkettung \(h=g\circ f\) kann man als senkrechte
Projektion der Parabel auf die Raumfläche auffassen. \(h\) ist, wie im
Text ausgerechnet, die (rote) räumliche Parameterkurve mit \(x(t)=2t^2\),
\(y(t)=t\) und \(z(t)=10 t^5\).
b) Der (orangefarbene) Tangentenvektor an die (grüne) Parabel \(f\) für \(t=2\) ist \(\vec{t}=(4\cdot 2,\;1,0)^{\rm T}\). Der (violette) Tangentenvektor an die (rote) Kurve \(h\) in \(B=(8,2,320)\) ist \(\vec{v}=(8,\,1,\,800)^{\rm T}=(8,0,448){\rm T}+(0,1,352)^{\rm T}\). Dieses Bild ist im Vergleich zu a) um ca. \(180^\circ\) nach links gedreht.
kettenregel-ex.ggb
kettenregel-ex-b3.ggb
|
| Abschnitt 3.2.4 Seite 266 1. Auflage: 3.2.4.1 Seite 241 |
|
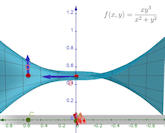
Abb. 3.14 Gemischte Ableitungen sind von
der Reihenfolge abhängig.
Im Bild ganz links ist die Funktion \(\frac{xy^3}{x^2 + y^2}\)
dargestellt zusammen mit \(f_x\) als Steigungsvektor an Punkt \(D\) über
Punkt \(C\) und \(f_y\) als Steigungsvektor an Punkt \(B\) über
Punkt \(A\). In der Mitte zeigt die Perspektive entlang der x-Achse,
dass \(f_y(x,0) \equiv 0\) ist. Das rechte Bild aus der Perspektive
entlang der y-Achse macht deutlich, dass \(f_x(0,y)\) mit \(y\)
anwächst. \(A\) und damit \(B\) lässt sich in der GeoGebra-Datei entlang der
x-Achse, \(C\) und damit \(D\) entlang der y-Achse verschieben.
SatzvonYoung.ggb
|
| Abschnitt 3.2.4 Seite 266 1. Auflage: 3.2.4.1 Seite 242 |
|
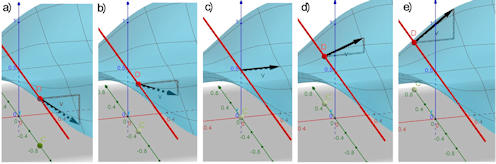
Abb. 3.15 Gemischte
Ableitungen im Detail.
Von links nach rechts ist in a) bis e) der Steigungsvektor zu
\(f_x(0,y)\) für \(y=-0.8,\ -0.4,\ 0,\ 0.4,\ 0.8\) gezeigt. Er steigt mit
\(y\) linear an.
SatzvonYoung.ggb
|
| Abschnitt 3.2.5 Seite 268 1. Auflage: Seite 244 |
|
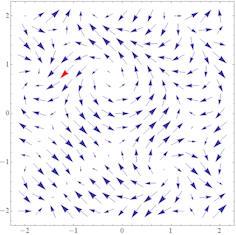
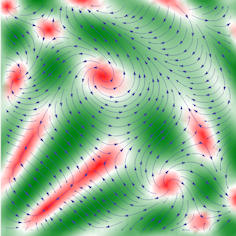
Abb. 3.16 Beispiel für ein Vektorfeld.
Links Vektoren an ausgewählten, gleichmäßig verteilten Stellen rund um
den Ursprung des \(\mathbb R^2\), rechts daraus
entstehende Stromlinien mit Färbung grün für hohe, rot für niedrige
Geschwindigkeit, wenn man die Vektoren als Geschwindigkeitsfeld deutet.
Bilder Div Curl, Mathematica Quelltext
 Dies zum Lesen und Verstehen
Dieses Notebook enthält noch viele weitere Beispiele zur Darstellung von Vektorfeldern. |
| Abschnitt 3.2.5.1 Seite 269 1. Auflage: Seite 245 |
|
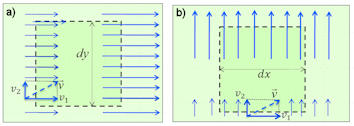
Abb. 3.17 Deutung der Divergenz eines Vektorfeldes.
Betrachtet wird die Materialbilanz für ein infinitesimales (grünes)
2d-Rechteck. Sie können sich das auch als 3D-Quader vorstellen.
Genaueres erklärt der Text.
|
| Abschnitt 3.2.5.1 Seite 270 1. Auflage: Seite 246 |
|
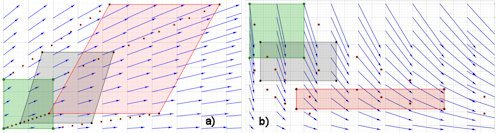
Abb. 3.18 Wirkung der Divergenz auf
Flächen. a) Divergenz ist positiv, mitfließende Flächen
vergrößern sich,
b) Divergenz ist konstant \(= 0\), mitfließende Flächen bleiben
erhalten, sie ändern nur ihre Form.
Vektorfeld-Div-2-linear.ggb
Vektorfeld-Div-0-(2).ggb
|
| Abschnitt 3.2.5.2 Seite 271 1. Auflage: Seite 247 |
|
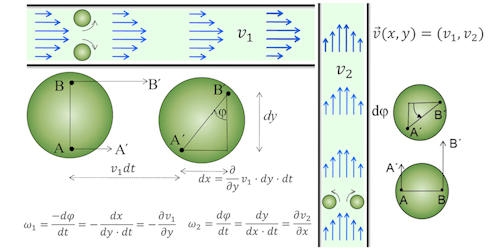
Abb. 3.19 Deutung der Rotation eines Vektorfeldes.
Die Erklärung dazu findet sich im Text.
|
| Abschnitt 3.2.5.3 Seite 272 1. Auflage: Seite 248 |
|
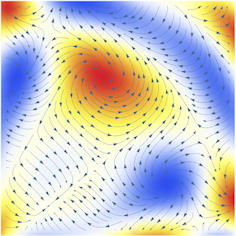
Abb. 3.20 Interessantes Vektorfeld, bei dem die Werte der
Divergenz und der Rotation farblich hervorgehoben sind. Links:
Divergenz, grün Materialsenken (\({\rm div}<0\)), pink Materialquellen
(\({\rm div}>0\)). Rechts: Rotation, blau im Uhrzeigersinn
(negative Winkel), rot gegen den Uhrzeigersinn (positive Winkel).
Bilder Div Curl, Mathematica Quelltext
Dies zum Lesen und Verstehen
Dieses Notebook enthält noch viele weitere Beispiele zur Darstellung von Vektorfeldern. |
| Abschnitt 3.2.5.3 Seite 273 1. Auflage: Seite 249 |
|
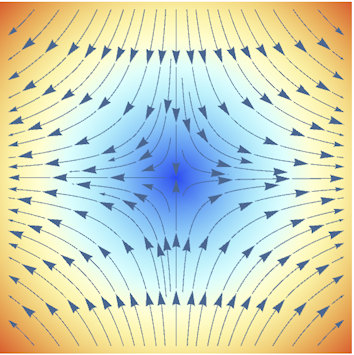
Abb. 3.21 Vektorfelder mit linearen
Funktionen. Sie zeigen alle Standardsituationen, bei denen die Divergenz die
Werte 0 oder 2 annimmt und auch die Rotation die Werte 0 oder 2 aufweist.
Man beachte, dass im 2D-Fall die Rotation ein Skalar, also eine Zahl ist. Die
Farben sind hier nur der Ästhetik wegen hinzugefügt, sie geben die Länge der
Vektoren wieder: blau für kurze, orange für lange Vektoren.
Bilder Div Curl, Mathematica Quelltext
Dies zum Lesen und Verstehen
Dieses Notebook enthält noch viele weitere Beispiele zur Darstellung von Vektorfeldern. |
| Abschnitt 3.2.5.4 Seite 274 1. Auflage: Seite 250 |
|
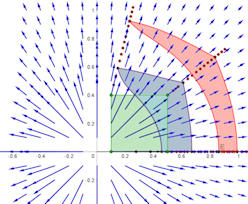
Abb. 3.22 Gradientenfeld
einer Zentralkraft. Das Potential ist so gewählt, dass nicht nur
(automatisch) die Rotation, sondern auch die Divergenz des
Vektorfeldes verschwindet.
Die farbigen Flächen sind deshalb alle
gleich groß. In der GeoGebra-Datei können Sie die Eckpunkte des grünen Rechtecks beliebig verschieben und sich den Effekt ansehen.
Vektorfeld-Div-zentral.ggb
Vektorfeld-Divergenz-anschaulich-zentral, Mathematica Quelltext
Dies zum Lesen und Verstehen
|
| 3.3 Optimierung einer Funktion zweier
Veränderlicher |
||
| Abschnitt 3.3 Seite 275 1. Auflage: Seite 251 |
|
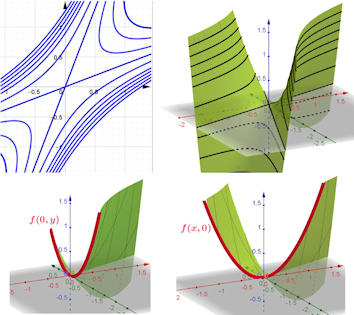
Abb. 3.23 Sattelpunkt für
\(f(x,y) = x^2+y^2-3xy\).
Die oberen Bilder zeigen den dreidimensionalen Verlauf der Funktion und die Höhenlinien, im Grundriss sind sie gedrehte Hypelbeln (blau). In der Datei entstehen Sie als Spuren bei Variation von \(c\). (Spuren löschen mit Strg f) Die darunter gezeigten Schnitte mit den Ebenen \(x=0\) und \(y=0\) können Sie in der Datei hinzuschalten.
fxySattel.ggb
|
| Abschnitt 3.3.3 Seite 279 1. Auflage: Seite 255 |
|
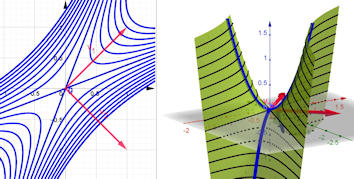
Abb. 3.24 Sattelpunkt und die Eigenvektoren der Hesseschen Matrix \(H_f\).
Dieses Bild setzt die Abb. 3.23 fort und wiederholt deren obere zwei Bilder, in die jetzt auch die Eigenvektoren von \(H_f\) eingetragen sind. Rechts sind auch die Schnittkurven durch die Fläche mit senkrechten Ebenen durch die Eigenvektoren gezeigt. Diese können hinzugeschaltet werden, sind in der Datei gelb und verlaufen durch die Punkte mit den stärksten Krümmungen der Höhenlinien, wie im Buch erläutert.
fxySattel.ggb
|
| Abschnitt 3.3.4 Seite 280 1. Auflage: Seite 256 |
|
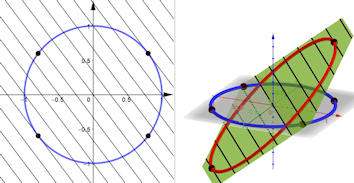
Abb. 3.25 Lineare Funktion auf
Kreis optimieren. Gezeigt sind die
Höhenlinien der Funktion
\(f(x,y) = 4x + 3y\),
die auf dem Kreis \(g(x,y) = x^2 + y^2 - 1 = 0\) optimiert
werden soll. Eingezeichnet sind die Punkte auf dem Kreis, in denen \(f\)
ein Minimum bzw. ein Maximum annimmt, sowie weitere Punkte, die im
Text erklärt werden.
optlinaufkreis.ggb
|
| Abschnitt 3.3.4.1 Seite 281 1. Auflage: Seite 257 |
|
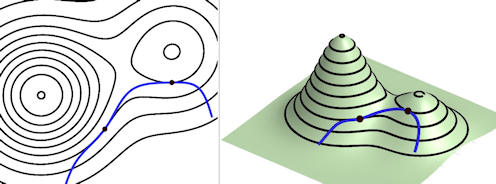
Abb. 3.26 Lagrange-Verfahren
demonstriert mit Höhenlinien. Das rechte Bild zeigt den Graphen einer
Funktion \(f(x,y)\) mit Höhenlinien, links die Höhenlinien allein in der
Ebene. Die Nebenbedingung \(g(x,y) = 0\) ist links als blaue Kurve,
rechts als "Wanderpfad" im Gebirge dargestellt. Die Objekte mit dem Index w beziehen sich auf das Gebirge und den Wanderpfad.
Punkt \(A\) mit dem Gradienten \(\vec{\nabla f}\) können Sie links frei ziehen. Damit wandern Sie mit \(A_w\) im Gebirge umher und es wird nochmals der Gradient (gelb) \(\vec{\nabla f}\) und die Richtungsableitung (rot) angezeigt. \(M_w\) ist das Maximum von \(f\) unter der der Nebenbedingung \(g(x,y)=0\). \(S_w\)ist ein Sattelpunkt.
optlagrange.ggb
|
| 3.4 Integrale 3D |
||
| Abschnitt 3.4.1 Seite 284 1. Auflage: Seite 260 |
|
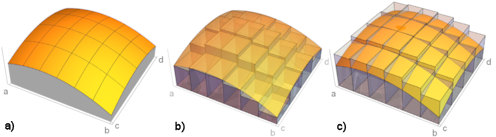
Abb. 3.27 Gebietsintegral.
a) Volumen, nach oben begrenzt durch
den Graphen von \(f\). b) und c) zeigen dazu
Riemann'sche Unter- und Obersummen aus Quadern.
int3d-fl-unter-ober, Mathematica Quelltext
|
| Abschnitt 3.4.1 Seite 285 1. Auflage: Seite 261 |
|
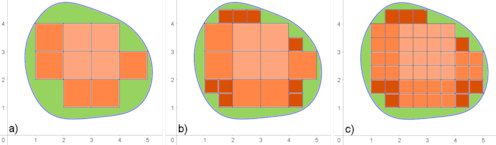
Abb. 3.28 Ausschöpfung eines krummlinig begrenzten Integrationsgebietes. a) große Rechtecke in der xy-Ebene, b) bessere Ausschöpfung durch zusätzliche kleinere Rechtecke, c) Verfeinerung der schon bestehenden Rechtecke. |
| Abschnitt 3.4.1.1 Seite 286 1. Auflage: Seite 262 |
|
Abb. 3.29 Mehrfachintegrale
als iterierte Integrale, von der
Quaderreihe über die Scheibe zum Blatt:
a) Eine Reihe von Quadern ist
eine Näherung für das Volumen einer Scheibe, die b) zeigt.
c) Wird nun die y-Achse immer feiner unterteilt, so erhält man im
Grenzfall ein Blatt an der festen Stelle \(y\).
int3d-fl-unter-ober, Mathematica Quelltext
Dies zum Lesen und Verstehen
|
| Abschnitt 3.4.1.1 Seite 288 1. Auflage: Seite 264 |
|
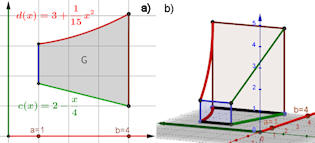
Abb. 3.30 Variable
Integrationsgrenzen. In a) ist das Integrationsgebiet mit den Funktionen,
deren Graphen das Gebiet begrenzen, zu sehen. in b) ist das prismenartige
Volumen gezeigt, dass das Integral auf der vorigen Seite berechnet.
Die Funktion ist \(f(x,y) = x\), eine Ebene, die die y-Achse enthält.
Fubini-Grenzen-variabel.ggb
|
| Abschnitt 3.4.1.2 Seite 289 1. Auflage: Seite 265 |
|
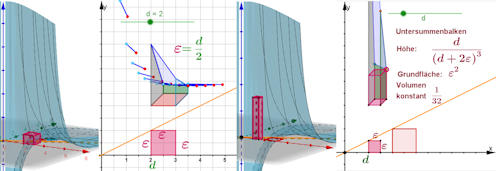
Abb. 3.31 Gegenbeispiel zum Satz von Fubini.
a) und c) Der Graph von \(f(x,y)\)
ist als blaue Raumfläche mit je einem Balken aus den Untersummen gezeigt.
b) und d) werden im Text erklärt. Es zeigt sich, dass
\(f\) über dem Gebiet \(0\le x\le 1,\ 0\le y\le 1\) nicht integrierbar ist.
Fubini-ab.ggb
Fubini-cd.ggb
|
| Abschnitt 3.4.1.2 Seite 290 1. Auflage: Seite 266 |
|
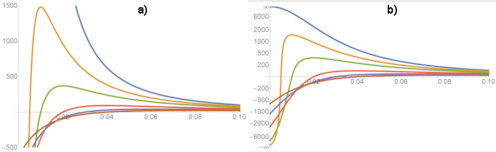
Abb. 3.32 Die Integration nach \(x\) bei festem \(y\).
a) Nahe bei \(y=0\):
Die Graphen im xz-System zeigen von oben nach unten \(x\mapsto f(x,y_0)\) für
\(y_0=0,\ 0.005,\ 0.01,\ 0.02,\ 0.03\) und \(0.04\).
b) Dasselbe, aber die z-Achse ist so gestaucht worden,
dass die "Werte" \(\infty\) und \(-\infty\) mit im Bild sind.
fubini-blaetter, Mathematica Quelltext
|
| Abschnitt 3.4.2 Seite 291 1. Auflage: Seite 267 |
|
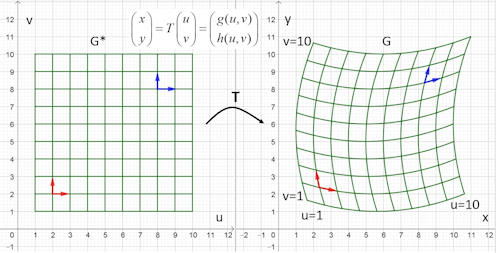
Abb. 3.33 Koordinatentransformation.
Nebeneinander sind die Gebiete \(G^*\) und \(G\) gezeigt, links dazu ein
gleichmäßiges Gitter parallel zu den uv-Achsen, rechts das gebogene Bildgitter
unter der Transformation \(T\).
Zwei kleine Rechtecke, geformt von blauen und roten Vektoren, und
deren Bilder als Rauten, sind auch eingezeichnet
Koordinatentransformation.ggb
|
| Abschnitt 3.4.2 Seite 292 1. Auflage: Seite 268 |
|
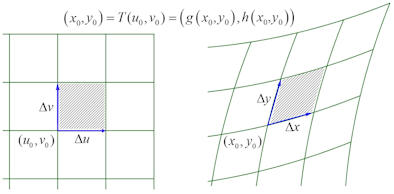
Abb. 3.34 Detail zu
Abb. 3.33. Ein von zwei kleinen Vektoren
\(\Delta u\) bzw. \(\Delta v\) parallel zu den xy-Achsen aufgespanntes
Rechteck und dessen Bild unter der Transformation \(T\) als krummlinige Raute in
den \(x,y\)-Koordinaten.
|
| Abschnitt 3.4.2 Seite 293 1. Auflage: Seite 269 |
|
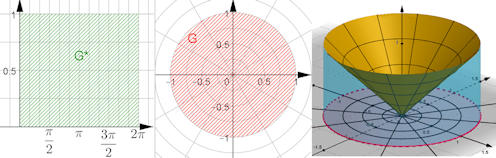
Abb. 3.35 Hohlkegel, Volumenberechnung
mit Koordinatentransformation auf Polarkoordinaten. Die Bilder zeigen von
links nach rechts: die Gebiete \(G^*\) und \(G\) und den Graphen der Funktion
\(f(x,y) = \sqrt{x^2+y^2}\) für den kopfstehenden Kegel.
Polarkoordinaten.ggb
Polarkoordinaten-kegel.ggb
|
| Abschnitt 3.4.3 Seite 294 1. Auflage: Seite 270 |
|
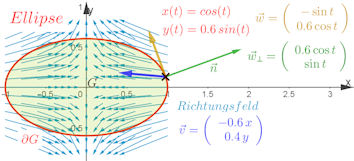
Abb. 3.36 Gebiet mit
parametrisiertem Rand in einem Richtungsfeld \(\vec v\).
Der Rand ist gegeben durch
\(\gamma(t)=(x(t),y(t))^{\rm T}\).
Ein Tangentialvektor des Randes ist \(\vec w=\gamma'(t)\).
Ein Normalenvektor auf dem Rand ist \(\vec{w}_\bot\), in normierter
Version \(\vec{n}\).
GaussBeispiel-Param-2dim.ggb
|
| Abschnitt 3.4.3 Seite 295 1. Auflage: Seite 271 |
|
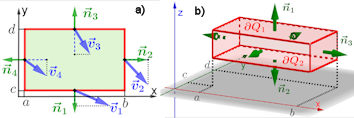
Abb. 3.37 Gauß'scher Satz für
Rechteck und Quader.
a) Summiert wird über die vier Ränder das Produkt von
\(\vec v_i\cdot\vec n_i\) mit \({\rm d} x\) bzw. \({\rm d} y\) .
b) Quadergebiet, zu summieren ist über alle sechs Flächen
\(\partial Q_1,\;\dots,\,\partial Q_6\).
GaussQuaderNeu.ggb
Gauss-RechteckNeu.ggb
|
| Abschnitt 3.4.3.1 Seite 298 1. Auflage: Seite 274 |
|
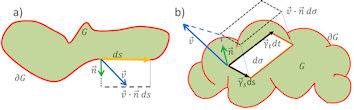
Abb. 3.38 Gauß'scher Satz,
Flussbilanz durch den Rand.
a) Bogenelement \({\rm d} s=\sqrt{x'(t)^2+y'(t)^2} {\rm d} t
=||\vec\gamma\,'(t)||{\rm d} t\)
b) Flächenelement \({\rm d}\sigma
= ||\vec\gamma_s\times\vec\gamma_t||\,{\rm d} s\,{\rm d} t\)
|
| Abschnitt 3.4.3.2 Seite 301 1. Auflage: 3.4.3.1 Seite 277 |
|
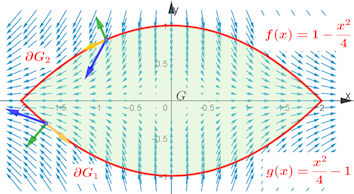
Abb. 3.39 Gauß'scher
Satz im 2D-Beispiel mit Randfunktionen.
Beim Vektorfeld \(\vec v=(x,-2y)^{\rm T}\) ist die Divergenz
\(\vec\nabla\cdot\vec v=1+(-2)=-1\), also konstant negativ.
Das Flächenelement ist \({\rm d} F = {\rm d} x\,{\rm d} y\), die Quellenbilanz also
\(\int_G (-1){\rm d} x\,{\rm d} y\). Wegen \(f(x)=-g(x)\)
ist das einfach
\(\int_{-2}^2(-2f(x)){\rm d} x = -\frac{16}{3}\).
GaussBeispiel2dimB.ggb
|
| Abschnitt 3.4.3.2 Seite 301 1. Auflage: 3.4.3.1 Seite 277 |
|
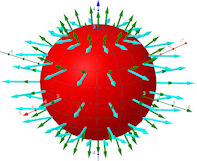
Abb. 3.40 Gauß'scher
Satz im 3D-Beispiel mit parametrisierter Randfläche.
Beim Vektorfeld \(\vec v=(\frac{\varrho}{r}x,\frac{\varrho}{r}y,0)^{\rm T}\) ist die
Divergenz \(\nabla\cdot\vec v=2\frac{\varrho}{r}\),
also konstant positiv (für \(\varrho\ge 0)\).
Die (blauen) Vektoren des Feldes sind alle parallel zur Grundebene radial zur
z-Achse angeordnet. Im Bild ist \(\varrho=2\), in den Punkten \(\vec\gamma(s,t)\)
der Kugeloberfläche sind sie \(2r\cos t\) lang. Da sie stets
nach außen weisen, ist klar, dass die Fluss- und Quellenbilanz positiv sein
werden. Die Quellenbilanz errechnet sich zu
\(\int_{\rm Kugel}(2\frac{\varrho}{r}) {\rm d} V = 2\frac{\varrho}{r} V_{Kugel}
= 2\frac{\varrho}{r}\frac{4}{3}r^3\pi = \frac{8}{3}\varrho r^2\pi\)
gauss-kugel.ggb
|
| Abschnitt 3.4.3.2 Seite 302 1. Auflage: 3.4.3.1 Seite 278 |
|
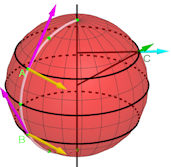
Abb. 3.41 Kugel in
Parameterdarstellung mit Tangentenvektoren. Zu Punkt \(C\) aus
Abb. 3.40 ist ein \(\vec n\) in Grün und ein \(\vec v\) in Hellblau
gezeigt. In der Parametrisierung der Kugeloberfläche \(\vec\gamma(s,t)\)
(siehe Text)
ist der Parameter \(s\) für die Breitenkreise zuständig, und mit \(t\) erreicht man
die halben Längenkreise, die dann vom Parameter \(s\) um die z-Achse gedreht
werden. In jedem Kugelpunkt stehen die Längenkreise senkrecht auf den
Breitenkreisen. Beim Äquator ist \(t=0\), in \(A\) ist \(t=\frac{\pi}{3}\), in \(B\)
ist \(t=-\frac{\pi}{3}\). In beiden Punkten ist der Tangentialvektor an
den Längenkreis nach oben gerichtet, denn die z-Koordinate von \(\vec\gamma_t\)
ist als \(r\cos t\) unabhängig vom Vorzeichen von \(t\).
gauss-kugel-tangenten.ggb
|
| Abschnitt 3.4.4 Seite 303 1. Auflage: Seite 279 |
|
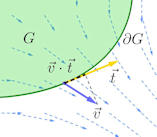
Abb. 3.42 Satz von Stokes im
\(\mathbb R^2\). Diesmal wird für das Integral entlang \(\partial G\) das
Vektorfeld auf den normierten Tangentialvektor \(\vec t\) projiziert.
StokesR2.ggb
|
| Abschnitt 3.4.4 Seite 305 1. Auflage: Seite 283 |
|
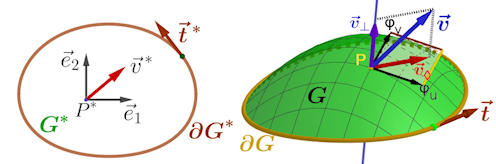
Abb. 3.43 Satz von Stokes im
\(\mathbb R^3\). Die Abbildung \(\varphi: G^* \to \mathbb R^3\) bildet
\(G^*\in\mathbb R^2\) auf das Flächenstück \(G\) im \(\mathbb R^3\) ab. Die
Koordinaten in \(\mathbb R^2\) heißen \(u\) und \(v\). Es ist
\(\varphi(\partial G^*) = \partial G\) und \(\varphi(P^*) = P\). Vom
Vektorfeld \(\vec v\) ist nur ein Vektor exemplarisch gezeigt. Seine
Projektion auf die Tangentialebene in \(P\) ist \(\vec v_\lozenge\),
bezogen auf die Basis \(\{\varphi_u,\varphi_v\}\). Bezieht man ihn auf
die Basis \(\{\vec e_1,\vec e_2\}\) am Punkt \(P^*\in G^*\), so erhält man
den Vektor \(\vec v\,^*\). Alle diese Vektoren bilden ein Vektorfeld in \(G^*\).
StokesR3.ggb |
|
|||||||
 Prof. Dr. Dörte Haftendorn
| Prof. Dr. Dieter Riebesehl
| Dipl.-Math. Dipl.-Ing. Hubert Dammer
|
|||||
