Höhere Mathematik sehen und verstehen

Springer Spektrum ISBN 978-3-662-62576-7
ISBN 978-3-662-62577-4 e-book
www.mathematik-sehen-und-verstehen.de
https://masuv.web.leuphana.de 		Dörte Haftendorn

Dieter Riebesehl

Hubert Dammer
1.5 Darstellungsvielfalt und Funktionstypen in 01 Analysis 2D  

1.5.1 Darstellungsvielfalt
Im Buch nur Text Vorlesung 5, zu den Redenweisen und zum Verständnis werden Ihnen Folien 1 bis 9 vermutlich helfen, Speziell gibt es dort auch Erkärungen zur Stetigkeit.
Überhaupt sind die Vorlesungen 5 bis 8 für die Analysis interessant. 		Auf der Kurven-Site gibt es das Kapitel 02 Werkzeug, in dem ausführlich auf alle Darstellungsarten und ihre Realisierung in GeoGebra eingegangen wird: Kurven und Funktionen, Polarkoordinaten, Parameterdarstellung, 3D-Darstellung
1.5.2 Stetigkeit
Abschnitt
1.5.2
Seite 29
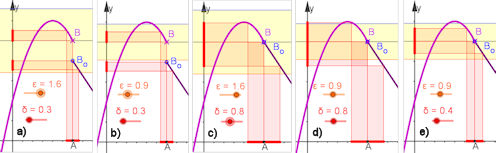
Abb. 1.17 Stetigkeit gemäß Definition 1.8. Genaue Erläuterung erfolgt im Text.


stetigkeit-buch-hoema.ggb
Stetigkeit im GeoGebra-Book
1.5.3 Funktionstypen
Wir empfehlen folgende Vorgehensweise:
In einem Tab Ihres Browsers hantieren Sie diese Website mit dem grünen Menu, in einem anderen Tab die Website mit dem blauen Menu.
In eigener Regie entscheiden Sie, ob Ihnen das hier Angebotene hinreichend verständlich ist oder ob Sie weitere elementarere Anregungen auf der blauen Site hilfreich finden.
Die Vorlesungen können Sie in pdf-Präsentation oder übersichtlich in der Handzeittel-Version ansehen. Die pptx-Datei baut die Folien schrittweise auf, das ist didaktisch besser. Auch das Skizzieren von Hand und Ihre Selbsttätigkeit wird von den Vorlesungen besonders unterstützt. Verbale Hilfen sind leider nicht dabei. Schließlich haben wir die beiden Bücher ja geschrieben, weil eben Worte auf Webseiten oftmals zu knapp sind.
Wenn etwas besonders lohnt machen wir darauf durch oder aufmerksam und setzen auch einen Link, entsprechend auch für die anderen Sites. Das grüne Bild führt hierhin zurück.
Abschnitt
1.5.3.1
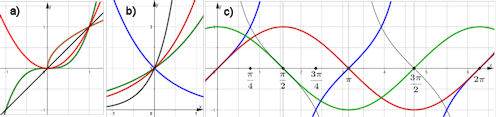
Seite 31		 Abb. 1.18 Grundfunktionen.
a) Potenz-Funktionen \(p_k(x)=x^k\) für \(k=1,2,3,\frac{1}{2}\).
b) Exponential-Funktionen \(f_k(x)=k^x\) für \(k=2,e,10,\frac{1}{e}\).
c) Trigonometrische Funktionen mit den Termen \(\sin x,\,\cos x,\,\tan x,\,\cot x\)in den Farben rot, grün, blau, grau.
  a)Potenzfunktionen Potenzfunktionenfunktionen \(k \not\in {\mathbb Z}\) ,     alle Potenzfunktionen: uneigentlich-potenzen.ggb, Datei dient eigentlich Abb. 1.56.
b) Exponentialfunktionen siehe auch unten Abb. 1.19 Die Fomenvielfalt ist gering, umso größe ist ihr Wachstum und ihrer Wichtigkeit.
Die Begründung für die Besonderheit der Basis e beruht auf ihrer besonderen Ableitung. Siehe mit Beweis im im Abschnitt 1.6 Differenzialrechnung
c)Trigonometrische Funktionen werden im Anschluss aufgegriffen.
Zusatz
zu Abschnitt
1.5.3.2
Seite 31

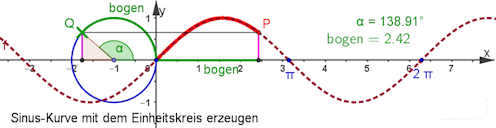
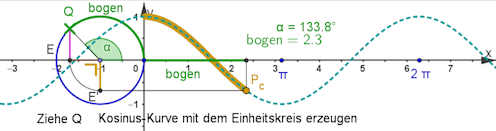
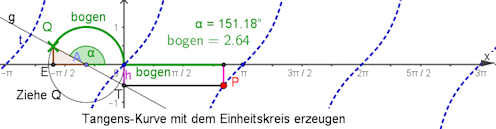
Die Entstehung der trigonometrischen Funktionen aus der Drehbwegung ist die tiefere Ursache dafür, dass diese Funktionen in der mathematischen Behandlung der Drehbewegungen und der periodischen Vorgänge fast immer auftauchen.
sinus_einheitskreis-buch.ggb

Sinusfunktionen von Hand zeichnen. Dabei geht es darum, dass man eine zutreffende Vorstellung der Gestalt der Kurven \(y=\sin(x), y=\sin(x-4)+2, \dots\) bildet. Dieses gilt auch für Cosinus. sinus_von_hand.ggb Mehrere Perioden kann man auf diese Weise nur zeichnen, wenn man die Achse mit Vielfachen von \(\pi\) beschriftet.


cosinus_einheitskreis-buch.ggb
tangens_einheitskreis-buch.ggb
Abschnitt
1.5.3.3
Seite 32		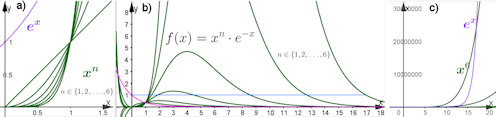 Abb. 1.19 Die e-Funktion wächst stärker als alle Potenzfunktionen.
a) Die vier Potenzfunktionen mit \(x^3,\dots,x^6\) werden für etwas größere x-Werte von der Funktion \(e^{x}\) geschnitten. Es ist dann nämlich \(e^x=x^n \iff x^n\cdot e^{-x}=1\).
In b) sind gerade die Funktionen \(x^n\cdot e^{-x}\) dargestellt. An den Stellen, an denen sie die Gerade \(y = 1\) schneiden, sind in a) Schnittpunkte der Exponentialfunktion mit der entsprechenden Potenzfunktion. Aber alle Funktionen \(x^n\cdot e^{-x}\) haben offenbar einen weiteren Schnittpunkt mit \(y = 1\) und zwischen diesen ein Maximum. Damit ist zu sehen, dass die e-Funktion letztlich doch schneller wächst als die Potenzfunktionen.
c) zeigt, dass die Funktion \(e^x\) die grüne Potenzfunktion \(x^6\) für \(x\approx 17\) „überholt“. Dem entspricht in b) das rechte Ende der blauen Linie. GeoGebra liefert auf numerischen Weg für den Schnittpunkt die Abszisse \(x = 17\) und die Ordinate \(24\,128\,091,75\) also knapp 25 Millionen. Es ist unmittelbar klar, dass es höheren Potenzen nicht anders ergeht.
e-staerker.ggb      e-staerker-gross.ggb    
1.5.3.4 Polynome
In dem ersten Buch "Mathematik sehen und verstehen" und in der dort zugrundeliegenden Vorlesung nahmen Polynome -- wohlverdient und gut überlegt -- einen großen Raum ein. In der dritten Auflage sind sogar noch die Aspekte "Polynome im Affenkasten" und "Quotienten aus Polynomen" hinzugekommen. Darum sind sie in diesem Buch auf einen Unterabschnitt reduziert.
Auch auf dieser Website wollen wir die Teile nicht doppeln, sondern sinnvoll verlinken.
Dabei ist es unvermeidlich, dass wir bei dem mathematischen Handwerkszeug auch auf Differenzierung und Integration vorgreifen müssen. Aber es sind nur elementare Kompetenzen nötig, die wir bei unseren Nutzern wohl voraussetzen können.
Abschnitt.
1.5.3.4
Seit34		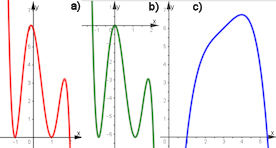 Man nennt c) ein Polynom mit Plattstelle, wir haben dieses Beispiel in Abb. 1.66 aufgegriffen. Abb. 1.20 Drei Polynome, die verschiedene Methoden erfordern.
Für a) ist die Gleichung bekannt: \(f(x)=3(x+1)^2(x-1)^2(x-2),\) man kann den Graphen aus dem Term mit den zwei doppelten Nullstellen und der einfachen Nullstelle sofort ohne Rechnung qualitativ zeichnen.
Bei b) und c) könnte man aus dem Funktionsterm nicht auf einen qualitativ guten Graphen kommen.

Zu a) und b) poly-erkennen.ggb
Polynome und ihre Linearfaktoren. Das Verstehen und die Fähigkeit, eigenständig qualitativ zu skizzieren und umgekehrt aus Graphen von Polynomen Gleichungen aufzustellen, war klausurrelevant für die Vorlesung, aus der das Buch "Mathematik sehen und verstehen" hervorgegangen ist. Es ist in Vorlesung 7 ausführlich vorgeführt.
Polynome im Affenkasten
1.5.3.5 Hyperbolische Funktionen
Abschnitt
1.5.3.5
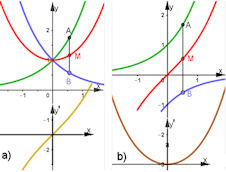
Seite 36		 Abb. 1.21 Hyperbolische Funktionen.
a) Der Cosinus hyperbolicus cosh ist die Mittenfunktion aus der e-Funktion und ihrer Kehrwertfunktion. Es gilt für die Ableitung: cosh' = sinh.
b) Der Sinus hyperbolicus sinh ist die Mittenfunktion aus der e-Funktion und ihrer gespiegelten Kehrwertfunktion. Es gilt für die Ableitung: sinh' = cosh.
sinh-cosh.ggb
Beweis der Ableitungs-Behauptungen unter Verwendung von \((e^x)'=e^x\):
\(f'(x)=\left(\frac{1}{2}\left(e^x\pm e^{-x}\right)\right)'= \frac{1}{2}\left(e^x\mp e^{-x}\right)\),
obere Vorzeichen \(\cosh'{x}=\sinh{x}\), untere Vorzeichen \(\sinh'{x}=\cosh{x}\)
Abschnitt 1.5.3.6
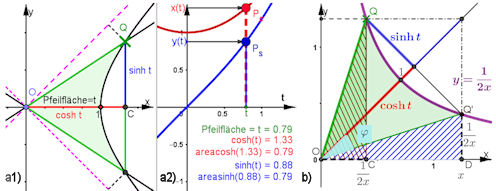
Seite 38		 Abb. 1.22 a1) Die Pfeilfläche \(F_{OQQ'}\) ist in b) enthalten in der Fläche, die aus der Integralfläche über die Hyperbel von C bis D und dem braun schraffierten Dreieck \(\Delta OQC\) gebildet wird. Subtrahiert man das kongruente blau schraffierte Dreieck \(\Delta OQ'D\), bleibt genau die Pfeilfläche \(F_{OQQ'}\) übrig.
a2) zeigt die relevanten Funktionen in Abhängigkeit von t.

Area_funktionen_Buch.ggb
arsinhAlsFlaeche-Buch.ggb
Wie im Buch erläutert, tragen diese Funktionen also zu recht den Beinamen hyperbolicus und ihre Umkehrfunktionen heißen zu recht Area-Funktionen, da sie eine Fläche, area, angeben.
 
1.5.4 Funktionen-Bauhof
Abschnitt
1.5.4.1
Seite 39		 Abb. 1.23 Addition zweier Funktionen g und h und Achsenstreckungen,
a)\(f(x)=g(x)+h(x)\)
b)\(f(x)=a\cdot g(x)\)
c)\(f(x)=g(k\cdot x)\) \text{ bei } |k|>1
d)\(f(x)=g(k\cdot x)\) \text{ bei } |k|<1
Hier und in Abb. 1.24 sollen die schraffierten Flächen lediglich das Verstehen unterstützen.
Abschnitt
1.5.4.1
Seite40		 Abb. 1.24 Verschieben von Funktionen
um \(\vec v=\left(\begin{smallmatrix}a\\b\end{smallmatrix}\right)\) durch \(f_{\vec v}(x)=f(x-a)+b\)
      bei Funktionen-Bauhof
Abschnitt
1.5.4.3
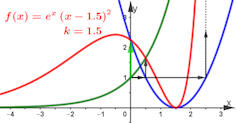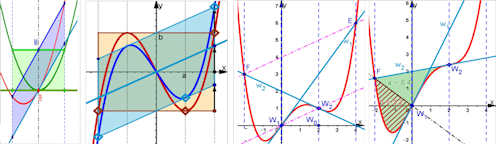
Seite 41		 Achtung: diese Funktion kann Grundlage für eine sehr lohnende Analysis-Aufgabe sein. Abb. 1.25 Für alle Produkte von Funktionen gilt:
Nullstellen setzen sich durch, d.h. an jeder Nullstelle des einen oder des anderen Faktors ist die Produktfunktion natürlich Null.
Andere Nullstellen der Produktfunktion gibt es nicht.
Einserstellen markieren Schnittpunkte, denn Stellen, an denen ein Faktor die Ordinate 1 hat, sind Schnittstellen des anderen Faktors mit dem Produkt.
An Minus-Einserstellen wird zusätzlich an der x-Achse gespiegelt.
Zusatz Qualitative Graphen von Hand durch Beachtung der Nullstellen, Einserstellen und der Vorzeichen. Als Hilfe dient das Felderabstreichen, man schraffiert das Gebiet, in dem die Egebnisfunktion NICHT velaufen kann.
In den folgenden Dateien können Sie das sehen. Wenn Sie die farbigen Striche löschen (im Algebrafenster auf klicken und Entf.), dann können Sie ihre eigenen Funktionen eintragen und selbst Striche machen (1. Menu-Icon, unten).
Summe freie Summe     Differenz freie Differenz     Produkt freies Produkt     Quotient freier Quotient Für alle:
Abschnitt
1.5.4.3
Seite41		 Abb. 1.26 Für alle Kehrwerte von Funktionen mit \(f(x)=\frac{1}{g(x)}\) gilt:
Nullstellen von g werden Polstellen von f, g und f haben stets dasselbe Vorzeichen.
a) und c) Wechselt g an der Nullstelle a das Vorzeichen, dann hat f an der Stelle a einen Pol mit Zeichenwechsel.
b) Es sind die Parabeln g und (gestrichelt) -g zu sehen. Sie berühren an der Stelle a die x-Achse, ihre Kehrwert-Funktionen haben dann an der Stelle a einen Pol ohne Zeichenwechsel.
Kehrwertfunktionen, Quotientenfunktionen, speziell auch Polynomquotienten Die Abschnitte 6.3.4, bis 6.3.6 sind für die 3. Auflage zu dem Buch hinzugekommen. Dort sind sie ausführlich behandelt, insofern lohnt es sich besonders, im Buch selbst zu lesen. Auf der Website sind daher die Erklärungen knapp gehalten.
In den GeoGebra-Dateien wird häufig von den Möglichkeiten eines zweiten Grafikfensters Gebrauch gemacht. Die Arbeit von Hand wird deutlich unterstützt.
Abschnitt
1.5.4.4
Seite 42		 Abb. 1.27 Stetige Fortsetzungen werden in allen Grafikfenstern (der Mathematikprogramme) gezeichnet, ohne dass eine Definitionslücke bemerkt wird. Keine der gezeigten Funktionen ist für \(x = 0\) definiert. Wollen Sie aber einen Wert an der Stelle anzeigen lassen, so ergigt sich korrekt: "undefiniert".
Nur e) hat einen Pol bei \(x=0\), da der Zähler dort nur eine einfache Nullstelle hat, der Nenner aber eine doppelte. Die Funktion ist daher nicht stetig fortsetzbar.
stetig-forts.ggb
Abschnitt
1.5.4.4
Seite 44		 Abb. 1.28 Stetige Fortsetzung bei Polynomen.
Sie sehen die Graphen von \(f=\frac{h}{g}\) (rot) mit \(h(x) = (x-1)(x-b)^\alpha (x-3)\) (grün) und \(g(x)=x(x-2)^\beta\) (blau) in Variationen der Vielfachheiten \(\alpha\) und \(\beta\) und (in d)) der mittleren Nullstelle \(b\) von \(h\).
a) \(\alpha=2,\, \beta=1,\,b=2:\qquad f^*(2)=0\), die stetige Fortsetzung $f^*$ ist rot.
b) \(\alpha=1,\, \beta=2,\,b=2:\qquad\) Pol bei \(x=2,\ f=f^*\), beide sind dort nicht definiert.
c) \(\alpha=1,\, \beta=1,\,b=2:\qquad \ f^*(2) = -\frac{1}{2}\), die stetige Fortsetzung \(f^*\) ist rot.
d) \(\alpha=1,\, \beta=1,\,b=2:\qquad\) und für \(b\in \{1.4,\,1.6,\,1.8\}\) violette Graphen von außen nach innen, \(b=2\) und \(f^*(2)=-\frac{1}{2}, \ f^*\) (rot) ist identisch mit c),
und für \(b\in \{2.2,\,2.4,\,2.6,\,2.8\}\) rosafarbene Graphen von innen nach außen.
Für alle genannten \(b\neq 2\) hat \(f\) eine Nullstelle bei \(x=b\) und einen Pol bei \(x=2\).
Alle Graphen von \(f\) haben bei \(x=0\) einen Pol mit Zeichenwechsel und einen Ast im 3. Quadranten, der hier nicht dargestellt ist.
poly-stetig-fortsetzung.ggb
Verkettung in besonderer Visualisierung
Abschnitt
1.5.4.5
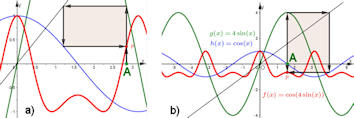
Seite 44		 Abb. 1.29 Verkettung von Cosinus und Sinus mit \(f(x)=\cos(4\sin(x))\):
Start \(A=(x,0)\longrightarrow z=g(x)=4\sin x\longrightarrow z=x\longrightarrow\)
\(\longrightarrow h(z)=\cos z\longrightarrow (x,f(x)) = (x,\cos(4\sin(x))\).
Am Startpunkt \(A\) kann man ziehen, Endpunkt \(P\) zeichnet dann seine Ortskurve, nämlich die verkettete Funktion.

verkettung-cos4sin.ggb
  Bei dieser Handlungsweise hängt an \(A\) stets eine "`Rechteckfahne"', die das Verstehen der Zusammenhänge ermöglicht. So kann man erkennen, warum \(f\) in der gezeigten Stellung ein Maximum hat, kann untersuchen, wo die beiden Minima liegen, kann beobachten, dass sie bei Verringerung der Amplitude 4 verschwinden und untersuchen, für welche Amplitude das passiert. So kommt man auf Ideen, und für Manches gelingt dann auch eine exakte Berechnung.
1.5.5 Komplexe Funktionen verbiegen Gitter
Diese steht auf dieser Website bei den Grundlagen zu komplexen Zahlen als Weiterführung.
1.6 Differentialrechnung und Funktionen untersuchen haben eine eigene Leitseite
Website zum Buch: Höhere Mathematik sehen und verstehen 01 Analysis 2D   START und TIPPS     Liste der Zusätze Erstellt: Dez.2020, Update 29. Juli 2021
 Prof. Dr. Dörte Haftendorn  Prof. Dr. Dieter Riebesehl  Dipl.-Math. Dipl.-Ing. Hubert Dammer