Mathematik sehen und verstehen,Website zum Buch

Höhere Mathematik sehen und verstehen

Springer Spektrum ISBN 978-3-662-62576-7
ISBN 978-3-662-62577-4 e-book
www.mathematik-sehen-und-verstehen.de

https://masuv.web.leuphana.de

Dörte Haftendorn

Dieter Riebesehl

Hubert Dammer

1.6 Differentialrechnung und 1.7 Funktionsuntersuchungen in 01 Analysis 2D

1.6.1 Steigung und Ableitung explizit kartesisch

Abschnitt
1.6.1
Seite 52

a) und b)

fahrradaufKurve_sekSteigFkt.ggb

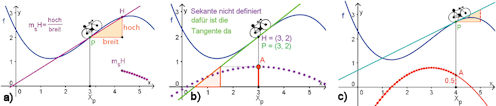
fahrradaufKurve_Ort-Ableitung.ggb

Abb. 1.35 Sekantensteigung und Tangente.
a) Zeigt eine Sekante bei festem $P$ mit ihrer Steigung bei beweglichem zweiten Punkt $H$. Unter $H$ ist mit violetten Punkten die Sekanten- steigung in Abhängigkeit von $x(H)$ dargestellt.
b) zeigt viele Punkte dieser Sekantensteigungs- funktion, die aber eine Definitionslücke für $h := x(H)-x(P) = 0$, d.h. $P = H$ hat. Die stetige Fortsetzung durch die als Grenzwert erhaltene Steigung der Tangente erlaubt das Zeichnen der Tangente.
c) zeigt nun mit der Ordinate von $A$ Tangentensteigungswerte bei variablem $P$ an. Die rote Kurve ist $f'$ , die Ableitung von $f$. Das in GeoGebra konstruierte Fahrrad zeigt bei Bewegung von $P$ an seinem Hinterrad stets die Steigung von $f$ in $P$ an.

Zusatz

$f(x)=\frac{1}{10}(x+2)^2(x-2)(x-4)$

Interaktive Kurvendiskussion als Radtour
Alles, was üblicherweise ausgerechnet wird, kann GeoGebra angeben.
Mindestens ist das als Kontrolle hilfreich.
Mit dem CAS könnte man auch die Rechnungen prüfen. Dabei lässt man besser die Verschiebung "+2" fort, sie dient nur der Übersichtlichkeit.

ableitung_rad.ggb

Zusatz

Die Euler'sche Zahl e ist die Basis derjenigen Exponentialfunktion,
die in $ E=(0,1)$ die Steigung 1 hat. Aus dem folgenden Satz ergibt sich dann:

$ ( {\rm e}^x )'={\rm e}^x$

expfkt-diff.ggb

Hinführung zu dieser Erkenntnis

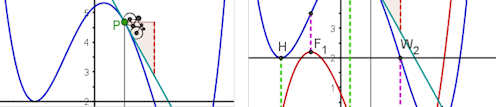
a) Erzeugung der Ableitung als Ortskurve, Vermutung, dass es sich um eine Stauchung handelt, Realisierung einer Stauchung
b) Einstellen des Stauchfaktors, so dass die Ableitung und die Stauchung zusammenfallen. Beobachtung, dass der Stauchfaktor und die Tangentensteigung in $ E=(0,1)$ übereinstimmen.
c) Einstellen der Basis, so dass Funktion und Ableitung aufeinanderfallen.

Zusatz

Satz: Die Ableitungen der Exponentialfunktionen $f(x)=a^x$ sind y-Achsen-Streckungen von ihr selbst. Der Streckfaktor ist die Steigung der Tangente in $ E=(0,1)$. Bei der Basis e ist er 1.
Beweis:
Der Differenzenquotient ist $ m_{sek}(x,h)=\frac{a^{x+h}-a^x}{h}=\frac{a^{h}-1}{h}\cdot a^x $. Der Bruch ist der von $x$ unabhängige Streckfaktor, es gilt $ \lim_{h \to 0}{\frac{a^{h}-1}{h}}=m_{tangente}(0) $, (siehe Bild b)).
Die Euler'sche Zahl e ist per definitionem die Basis, bei der der Streckfaktor 1 ist.

Abschnitt
1.6.1.2
Seite 54

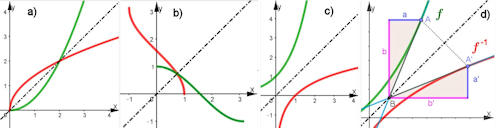
Abb. 1.36 Funktionen (grün) mit Umkehrfunktionen (rot).
a) $f(x)=\frac{1}{2} x^2 \iff f^{-1}(x)=\sqrt{2x\,} \mbox{ für }x \geq 0$,
b) $f(x)=\cos(x) \iff f^{-1}(x)=\arccos(x) \mbox{ für }0\leq x \leq \pi\mbox{ bzw. } -1\leq x\leq 1$,
c) $f(x)={\rm e}^x \iff f^{-1}(x)=\ln(x) \mbox{ für }x \in \mathbb R\mbox{ bzw. } x\ge 0,$
d) $f(x)={\rm e}^x-\frac{3}{4} \iff f^{-1}(x)= \ln(x+\frac{3}{4})$ und Erklärung für $f'(x)=\frac{b}{a}=\frac{1}{\frac{a'}{b'}}=\frac{1}{(f^{-1})'(y)}.$

Zusatz
Abschnitt
1.6.1.2
Seite 54

Freie Umkehrrelationen und Umkehrfunktionen, sie werden hier durch geometrische Achsenspiegelung erzeugt.

freieUmkehrrelation.ggb

Die Gleichungen der Umkehrrelationen lassen sich einfach durch Tausch von $x$ und $y$ schreiben.
Im Bild ist $y=\frac{1}{4}(x+2)^4$, daher ist die Umkehrrelation $x=\frac{1}{4}(y+2)^4$. GeoGebra zeichnet diese implizite Gleichung sofort.
Von GeoGebra wird aber eine Parameter-Gleichung angeboten, die mehrfach Nullen als Faktoren enthält. (Der Grund ist unklar.) Man kann sie einfach ernst nehmen, dann ergibt sich die Parameterdarstellung $x=\frac{1}{4}(t+2)^4$ und $y=t$, also die parametrisierte implizite Gleichung. Prinzipiell ist es klug, dass GeoGebra die Parameterdarstellung wählt.

1.6.2 Implizite Ableitung

Abschnitt
1.6.2.1
Seite 57

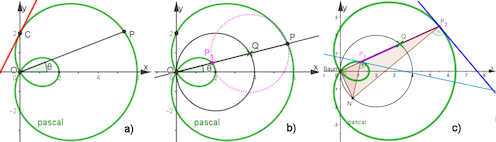
Abb. 1.37 Tangente an die Pascal'sche Schnecke mit $k=a=2$.
a) Die rote Tangente ist durch Ableiten der impliziten Gleichung bestimmt worden (siehe Text), weiter sind Polarradius und Polarwinkel für die Polardarstellung in Abschnitt 1.6.3.1 zu sehen.
b) zeigt darüber hinaus die Konstruktion der Pascal'schen Schnecke als Konchoide (siehe Abschnitt 1.6.3.3), und in c) ist eine geometrische Konstruktion der Tangente vorgeführt, die für alle Polarkurven gilt, siehe Abschnitt 1.6.3.2.
a) Im Buch ist die Gleichung der roten Tangente als $y=\frac{2a}{k}x+k$ hergeleitet.

b) Pascal'sche Schnecken als Konchoiden, speziell als Hundekurven mit Kreisstraße.

pascal-schnecke-koncho.ggb

c) Tangenten für die Pascal'sche Schnecken kann man auch rein geometrisch erzeugen.

pascal-schnecke-Tangenten.ggb

Beweis der Tangentenkonstruktion: Im Kurvenbuch ist gezeigt, dass in dem braunen Dreieck die Seite $\overline{ON}=r'(\theta)$ sein muss, damit die Senkrechte auf $\overline{NP}$ Tangente in $P$ ist. Siehe dazu hier Abb. 1.38. Dieses wird nun gezeigt: Der rechte Winkel bei $O$ garantiert, dass $\overline{NQ}$ Durchmesser des Wanderkreises ist. Dieser hat die Polargleichung $r(\theta)=2a\cos{\theta}.$ Damit hat die Pascal'sche Schnecke die Polargleichung $r(\theta)=2a\cos{\theta}\pm k$. Das hat $r'(\theta)=-2a\sin{\theta}$ als Ableitung der Schnecke zur Folge. Sei nun $O'$ der diametral gegenüber $O$ liegende Punkt des Wanderkreises. Dann ist $ONO'Q$ ein Rechteck, bei dem $\theta=\angle{ OO'N}$ ist, und mit $\overline{OO'}=2a$ gilt $\overline{ON}=2a \sin{\theta}$. q.e.d.

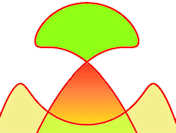Zunächst etwas zu den Konchoiden. Man nennt sie auch Hundekurven, denn man kann sich vorstellen, ein Mensch $Q$, nennen wir ihn Quo Vadis, wandere auf einer Straße, er habe zwei Hunde an zwei Leinen, $P_1$, genannt Pluto strebe stets einem Baum $O$ zu, $P_2$, genannt Fiffi, hat Angst von dem Baum und strebt fort.
Wenn die Straße eine Gerade ist, haben wir die Konchoide des Nikomedes, mit einem Kreis als Straße, die hier vorgestellten Pascal'schen Schnecken, auch Limacon genannt, man kann $Q$ auf jeder Kurve laufen lassen. Das Bild zeigt eine Konchoide mit Parabel-Straße.

Im Kurvenbuch finden Sie Geometrie und Analysis ineinander verwoben.

1.6.3 Parametrische Ableitung

Zusatz

Ellipsen zum Vergleich mit $a=3,\;b=2$
Violette Tangenten: Impizite Gleichung $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
Blaue Tangenten: Parameter-Gleichung $x=a\cos{t},\; y=b\sin{t}$
Grüne Tangenten: Polar-Gleichung $r(\theta)=\frac{p}{1-\varepsilon \cos{\theta}}$
Zusammenhang: $p=\frac{b^2}{a},\; \varepsilon^2=1-\frac{b^2}{a^2}$

Zusatz

Violett undBlau: ellipsenTangenten.ggb		Grün: ellipsenTangentenPolar.ggb
Implizite Ableitung: $\frac{2x}{a^2}+\frac{2y}{b^2}y'=0$ also $m_i=y'=-\frac{b^2 x}{a^2 y}$ Punkt $A$ auf impliziter Kurve, Schrittweite 0.25 (bei Eig.->Algebra)	Parametrische Ableitung: $\dot{x}=-a\sin{t},\;\dot{y}=b\cos{t}$ Tangentensteigung $m_t=\frac{\dot{y}}{\dot{x}}=-\frac{b\cos{t}}{a\sin{t}}$ Punkt $B=(a \cos{t},b\sin{t})$, t mit Schieberegler Schrittweite $\frac{\pi}{60}$	Polar-Ableitung aus $x=r(\theta)\cos{\theta},\;y=r(\theta)\sin{\theta}$ Tangentensteigung $m_p=-\frac{r'(\theta)\sin{\theta}+r(\theta)\cos{\theta}} {r'(\theta)\cos{\theta}-r(\theta)\sin{\theta}}$ Punkt $C=(r(\theta); \theta)$ im Polaren Gitter, Achtung: Semikolon!!!! $\theta$ mit Schieberegler Schrittweite $\frac{\pi}{60}$
Bei diesen drei Ellipsen werden die Tangenten auf verschiedene Art erzeugt, das führt zu dem unterschiedlichen Erscheinungsbild, aber auch zu anderem Verhalten an den Hauptscheiteln, bei denen die Tangenten parallel zur y-Achse sind. Im Einzelnen: a) Die Tangente ist mit Tangente(A,ell) erzeugt, dieses Tool hat kein Problem an den Scheiteln. Für den wandernden Berührpunkt $A$ sind die Pfeiltasten nacheinander von Scheitel zu Scheitel "Nord, West, Süd, Ost" verwendet. Die Autoren wissen nicht genau, wie GeoGebra die Schrittweite 0.25 umsetzt. Der Effekt ist sichtbar. b) Die Tangente ist mit der Punkt-Steigungsform mit $m_t$ erzeugt, bei $t=0,\ t=\pi$ wird tatsächlich keine Tangente gezeichnet (sichtbare Lücke), der Nenner von $m_t$ ist null. c) Hier ist mit der genannten Formel $m_p$ berechnet (für $r'(\theta)$ siehe CAS-Fenster). Auch hier ist der Nenner von für $t=0$ null. Jedoch wird für das Grafik-Fenster numerisch gerechnet, dadurch wird $\theta=\pi$ nicht exakt getroffen und GeoGebra zeigt ein $m_p$ von mehreren Billionen an, zeichnet aber eine (fast) Senkrechte. Ebenso geht es für $\theta=2\pi$. Darum fehlen hier die senkrechten Tangenten nicht.

1.6.3 Polare Ableitung

Abschnitt
1.6.3.2
Seite 59

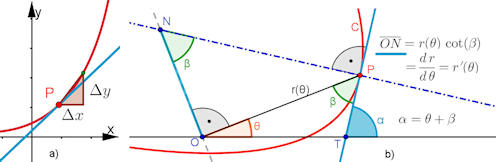
Abb. 1.38 Steigung und Tangente. a) Sekantensteigung und Tangente für die explizite kartesische Darstellung, b) Tangente und Normale für Polarkurven.

Auf der Kurven-Website sind die Formeln zusammengetragen. Vollständig bewiesen sind sie im zugehörigen Kurvenbuch S. 318f.
Die hier links gezeigte geometrische Konstruktion der Tangente ist in Abb. 1.37 c) bei den Pascal'schen Schnecken angewendet und dort im Zusatz bewiesen.
Rechnerisch und grafisch ist die polare Ableitung soeben im Zusatz zu den Ellipsen-Tangenten vorgeführt.

1.7 Funktionen untersuchen 1.7.1 Lokale Extremstellen

Abschnitt
1.7.1
Seite 61

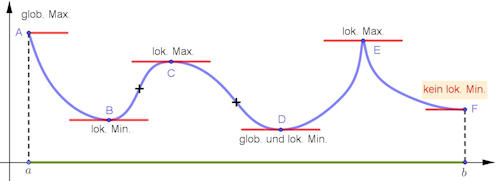
Abb. 1.39 Lokale versus globale Extrema. Für jeden der Punkte $A$ bis $F$ ist angegeben, um welche Art von Extremum es sich handelt. In jedem Punkt ist eine Parallele zur x-Achse gezeichnet, die die Extremaleigenschaft verdeutlicht, sie ist in $A$ und $E$ nicht Tangente. Die schwarzen Kreuze bezeichnen Wendepunkte, die in Abschnitt 1.7.4 besprochen werden.

ExtremumLokalGlobal.ggb

Zusatz

kurvendiskussion.ggb

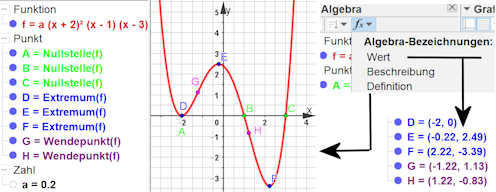
Kurvendiskussion Hier auf der Webseite haben wir - im Gegensatz zum Buch - den Platz, Ihnen eine übliche Kurvendiskussion vorzustellen und Ihnen die Unterstützung durch GeoGebra zu zeigen. Wir gliedern in die Teile 1.) und 2.). Im 7. Kapitel werden wir vor allem auf die kniffligeren Vorgehensweisen eingehen. Als Start öffen Sie das CAS-Fenster und definieren Sie die Funktion, die Sie untersuchen wollen, mit f(x):=.... Nur im CAS ist der Doppelpunkt nötig. Durch dieses Vorgehen haben Sie dann dieses auch im Algebrafenster. Andersherum hätten Sie zwei verschiedene Namen.
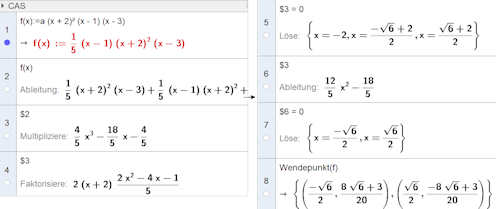
1.) Elementare Erkundung mit dem Algebra- und dem Grafikfenster. Legen Sie $a=0.2$ fest. So haben Sie später nun eine Steuerung für den Platzbedarf. Wie man solche "Form"-Parameter in CAS bewahrt, finden Sie hier. Nun ist $f$ im Algebrafenster bekannt und der Graph erscheint im Grafikfenster.
Wie Sie links sehen, braucht man nur die üblichen Ziele der Kurvendiskussion zu nennen, um sofort die entsprechenden Punkte auf dem Graphen zu bekommen. Deren Koordinanten erhält man, indem im rechten Pulldownmenu des Algebrafensters "Wert" wählt.
2.Symbolische Berechnung mit CAS: Es gibt das CAS-Menu

.
Seine Befehle werden auf den Ausdruck angewandt, der am Anfang einer CAS-Zeile steht. Z.B. steht in Zeile 3 $2 (für Zeile 2), geklickt wurde der Button mit den Klammern, das hat die Klammern in Zeile 2 (hier sind nicht alle zu sehen) aufgelöst und alles nach Potenzen von x zusammengefasst.
Aber es sind auch Befehle möglich, wie Zeile 8 zeigt.

1.7.2 Oszillierende Funktionen, Sinus-Wunderdinge

Abschnitt
1.7.2
Seite 63

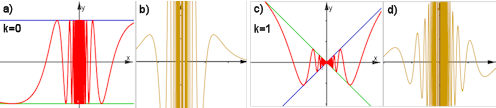
Abb. 1.40 Sinus-Wunderdinge: $f_k(x)=x^k\sin{\frac{1}{x}}$ und $f_k(0):=0$
a) Graph von $f_0$ und b) Graph von $f_0'$.$\qquad$ c) Graph von $f_1$ und d) Graph von $f_1'$.
$f_0$ ist unstetig, $f_1$ ist stetig, beide Ableitungen sind nicht beschränkt.

Für alle vier Bilder:

sinwunder-xksin1durchx.ggb

Abschnitt
1.7.2
Seite 63

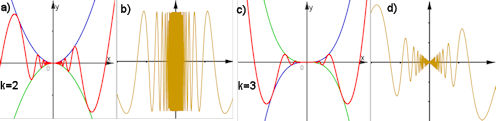Abb. 1.41 Sinus-Wunderdinge: $f_k(x)=x^k\sin{\frac{1}{x}}$ und $f_k(0):=0$}
a) Graph von $f_2$ und b) Graph von $f_2'$.$\qquad$ c) Graph von $f_3$ und d) Graph von $f_3'$.
$f_2$ ist differenzierbar, $f_2'$ zwar beschränkt, aber in 0 nicht stetig. $f_3$ ist stetig differenzierbar.

Abschnitt
1.7.2.1
Seite 65

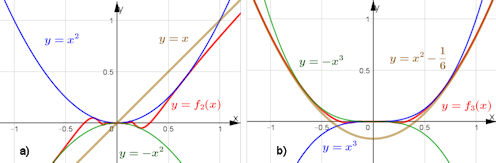
Abb. 1.42 Asymptoten für $f_k(x)=x^k\sin \frac{1}{x}$. a) Graphen von $f_2,\ y=\pm x^2,\ y=x$,
b) Graphen von $f_3,\ y=\pm x^3,\ y=x^2-\frac{1}{6}$. Gezeigt sind also jeweils die oszillierende Kurve (rot), die einhüllenden Potenzfunktionen (blau und grün) und die Asymptote (ockerfarben).

sinwunderAsymptoten.ggb

(ohne Einhüllende)

xksin1durchxAsymptote.ggb

1.7.3 Krümmungen

Abschnitt
1.7.3.1
Seite 66

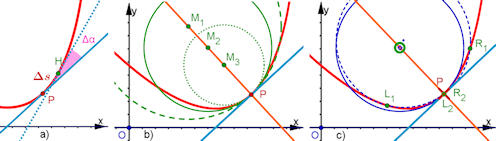
Abb. 1.43 a) Krümmung als Grenzwert von $\frac{\Delta \alpha}{\Delta s}$,
b) Krümmungskreis interaktiv mit der Normalen finden: Ziehe an den Mittelpunkten, welcher Kreis ist der intuitiv beste Krümmungskreis?
c) Krümmungskreis interaktiv als Kreis durch drei Kurvenpunkte finden (Schupp und Henn). Rücke einen linken Punkt L und einen rechten Punkt R (fast) auf P.
Der "Grenzkreis" müsste der Krünmmmungskreis sein.

kruemmungErkunden.ggb

1.7.4 Wendepunkte

Zusatz
Zu
Abschnitt
1.74
Seite 69

Hier fehlt ein Bild zum Zusammenhang mit der Krümmung. Evt. auch darüber noch was zur Evolute. Gemeinsamkeit: sowohl der Krümmungskreis als auch die Wendetangente durchsetzten die Kurve.

Zusatz Abb. 1.XYX Legende FETT BEACHTEN

Geogebra.ggb

1.8 Integralrechnung hat eine eigene

Leitseite

Website zum Buch: Höhere Mathematik sehen und verstehen 01 Analysis 2D START und TIPPS Liste der Zusätze		Erstellt: Dez.2020, Update 29. Juli 2021
Prof. Dr. Dörte Haftendorn	Prof. Dr. Dieter Riebesehl	Dipl.-Math., Dipl.-Ing. Hubert Dammer