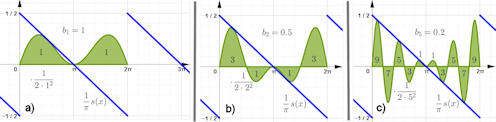
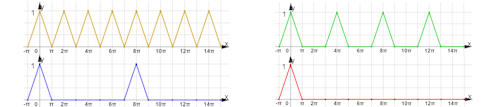
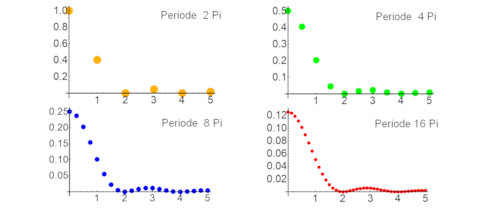
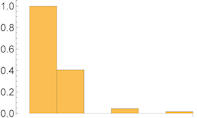
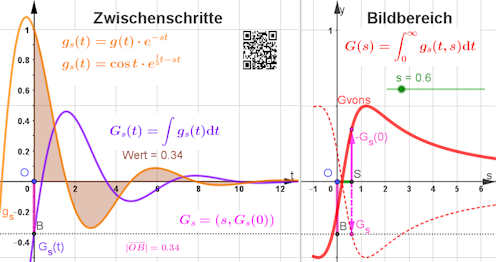
gitter-e-fkt.ggb
gitter-e-fkt.ggb

Abschnitt
1.5.5.1
Seite 48
Auflage 1:
Seite 46
|
|
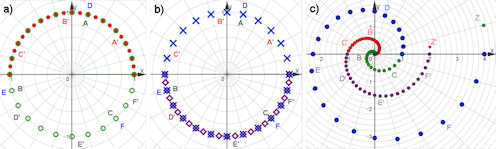
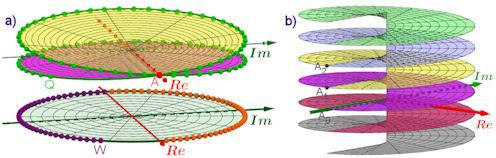
Abb. 1.31 Komplexe Wurzeln und Riemann’sche Fläche in Polardarstellung mit einer
Winkeleinteilung von \(\frac{\pi}{12}\)
a) Die grünen Punkte auf dem Einheitskreis haben die roten Punkte als
Wurzeln. Sie sind ausschließlich in der oberen Halbebene.
b) Die Punkte mit den blauen Kreuzen auf dem Einheitskreis des zweiten Blattes der Rie-
mann’schen Fläche, z.B. \(D\), haben die Punkte mit den violetten Karos als Wurzeln, also \(D_0\).
Sie sind ausschließlich in der unteren Halbebene.
c) Die Polarwinkel der Urbildpunkte und der Bildpunkte sind dieselben wie in a) und in b). Sie
haben dieselben Farben, die Radien sind aber stufenweise verändert, und zwar für die Urbilder (grün bzw. blau) auf einer Quadratspirale und daher für die Bilder, die Wurzeln daraus, mit linearem Radiuswachstum (rot bzw. violett).
Zu a) und b)
 komplex-einheitswurzel-polar.ggb
komplex-einheitswurzel-polar.ggb 

Zu c)
 komplex-einheitswurzel-polar-spirale.ggb
komplex-einheitswurzel-polar-spirale.ggb

 Die Interaktion ist bei der nachfolgenden Spirale überzeugender möglich.
Die Interaktion ist bei der nachfolgenden Spirale überzeugender möglich.
|
 Zusatz Zusatz |
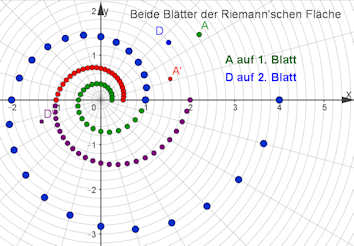 Wandern auf den beiden Blättern der Riemann'schen Fläche für die komplexe Wurzelfunktion.
Wandern auf den beiden Blättern der Riemann'schen Fläche für die komplexe Wurzelfunktion.
Über das Buch hinaus haben wir das rechte der drei vorigen Bilder nochmals gemacht und zwar nun mit einer e-Funktionsspirale,
sie heißt auch "logarithmische Spirale".
Auf diese Weise konnten wir deutlicher zeigen, dass die grüne Urbild-Spirale alle vier Quadranten durchläuft,
ihre Bild-Spirale aber nur in der oberen Halbebene Punkte hat. Die blauen Urbilder befinden sich dann auf dem 2. Blatt der
Riemannschen Fläche, wieder in allen vier Quadranten, ihre violetten Bilder sind ausschließlich in der unteren
Halbebene.
 komplex-einheitswurzel-polar-spirale-blaetter.ggb
komplex-einheitswurzel-polar-spirale-blaetter.ggb 

Hier kann man \(A\) auf dem 1. Blatt frei ziehen und sich \(A'\) ansehen. Entsprechend ist \(D \) auf dem 2. Blatt
mit passendem \(D'\).
|
Abschnitt
1.5.5.1
Seite 48
Auflage 1:
Seite 47
|
|
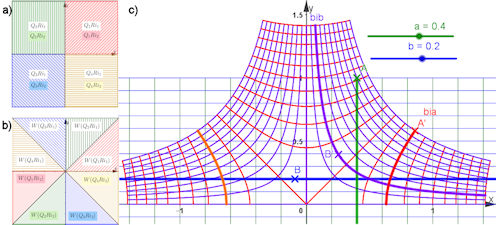
Abb. 1.32 Riemann’sche Flächen, a) für die Wurzelfunktion, b) für den Logarithmus.
a) Von Punkt A aus kann man in GeoGebra Punkt Q auf dem Rand des Einheitskreises des
oberen (gelben) Blattes wandern lassen, zeitgleich wandert die (orangefarbene) Wurzel W in der
(grünen) Gauß’schen Zahlenebene auf dem Einheitskreis. W ist erst auf der negativen reellen
Achse, wenn Q schon wieder bei A ist. Beim Weiterlaufen „taucht Q ab“ auf das 2. Blatt der
Riemann’schen Fläche, seine Wurzel W wird violett und W läuft nun Q voraus. Q holt aber
auf, beide erreichen gleichzeitig Punkt A auf der reellen Achse und wechseln gemeinsam wieder
auf das 1. Blatt.
b) Beim Logarithmus, siehe Abschnitt 1.5.5.2, würde sich Q auf dem Rand der teilweise gezeigten
Wendelfläche nach oben oder unten schrauben, bei jeder Umdrehung würde sein Argument \(2 pi\)
gewinnen oder verlieren.
Zu a)
 riemann-flaeche-wurzel-2.ggb
riemann-flaeche-wurzel-2.ggb

Zu b)
 riemann-flaeche-ln2.ggb
riemann-flaeche-ln2.ggb

|
Abschnitt
1.5.5.1
Seite 49
Auflage 1:
Seite 48
|
|
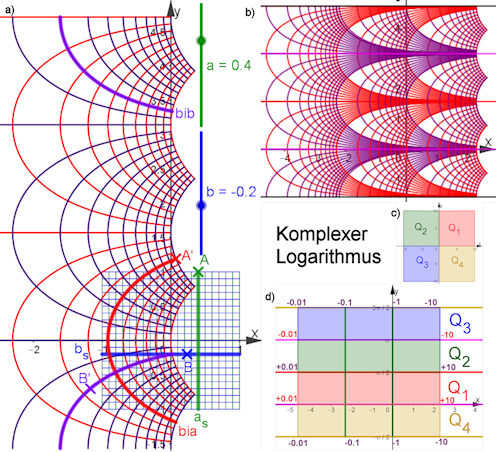
Abb. 1.33 a) Riemann’sche Fläche, 1. Blatt schraffiert, 2. Blatt unschraffiert gleichfarbig
unterlegt,
b) aus den Quadranten werden mit der Wurzelfunktion Dreiecke, oben schraffiert
Wurzeln vom 1. Blatt, unten unschraffiert vom 2. Blatt.
c) Gitterverbiegung der Wurzelfunktion
vom 1. Blatt, siehe Text.
 quadranten-wurzel.ggb
quadranten-wurzel.ggb

 gitter-wurzel.ggb
gitter-wurzel.ggb

|
Abschnitt
1.5.5.2
Seite 51
Auflage 1:
Seite 49
|
|
Abb. 1.34 Die Logarithmus-Funktion verbiegt das Gitter.
a) Für das grün-blaue Gitter [-1,1]×[-1,1] mit Linienabstand 0.1 sind alle Bildkurven gezeigt.
b) Für das nicht gezeigte logarithmische Gitter [-10,10] × [-10,10] mit gestuften Abständen
(siehe Text) entsteht aus jedem Quadranten ein Streifen mit Bildkurven.
c) Farbige Darstellung der Quadranten, deren Bildbereiche in d) zu sehen sind.
 gitter-ln-fkt-carc.ggb
gitter-ln-fkt-carc.ggb 
 quadranten-ln.ggb
quadranten-ln.ggb 
|
 Zusatz Zusatz |
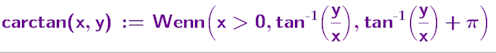
 Demonstration, wie man in GeoGebra eine Funktion definieren kann.
 carctan.ggb
carctan.ggb
|
Das Argument-Problem:
Von komplexen Zahlen im 2. Quadranten erwartet man man einen Polarwinkel \(\alpha\),
der \(\frac{\pi}{2}<\alpha<\pi\) erfüllt. Eine Berechnung mit dem Arcustanges der Steigung liefert aber einen negativen Winkel, zu dem man \(\pi\) addieren muss. Auch im 3. Quadranten ist diese Addition nötig. Im 4. Quadranten bezeichnen \(\alpha\)
und \(\beta\) als Polarwinkel denselben Punkt. Daher kann man dort wieder den Arkustangens nehmen.
Die in GeoGebra definierte Funktion liefert für \(0\leq\alpha<\frac{3}{2}\pi\) das \(\alpha\) und für
\(\frac{3}{2}\pi\leq \alpha < 2 \pi\) das \(\beta\). Damit ist die Ebene längs der negativen imaginären Achse "aufgeschlitzt".
GeoGebra hat auch, wie alle CAS, eine Funktion für das Argument einer komplexen Zahl \(z\), geschrieben arg(a+i b) oder für einen kartesischen Punkt \(Z\) arg(x(Z), y(Z)), die i.d.R. die Ebene längs der negativen x-Achse aufschlitzt.
Es existiert auch der Befehl abs(a+i b) bzw. abs(x(Z),y(Z)) für den Betrag von \(z\). (In der Befehlesammlung z.Z. nicht aufgeführt.)
Achtung, das i ist aus den Sonderzeichen zu nehmen, wie \(\alpha, \dots\).
|
 1.6 Differentialrechnung Weiter mit 1.7.
1.6 Differentialrechnung Weiter mit 1.7.
|
|
|
 1.6.1 Steigung und Ableitung explizit kartesisch 1.6.1 Steigung und Ableitung explizit kartesisch
|
Abschnitt
1.6.1
Seite 53
Auflage 1:
Seite 52

|
a) und b)  fahrradaufKurve_sekSteigFkt.ggb
fahrradaufKurve_sekSteigFkt.ggb 
c)  fahrradaufKurve_Ort-Ableitung.ggb
fahrradaufKurve_Ort-Ableitung.ggb 
|
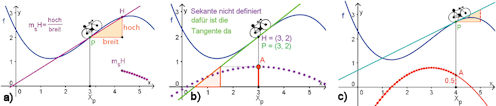
Abb. 1.35 Sekantensteigung und Tangente.
a) Zeigt eine Sekante bei festem \(P\) mit ihrer
Steigung bei beweglichem zweiten Punkt \(H\). Unter \(H\) ist mit violetten Punkten die Sekanten-
steigung in Abhängigkeit von \(x(H)\) dargestellt.
b) zeigt viele Punkte dieser Sekantensteigungs-
funktion, die aber eine Definitionslücke für \(h := x(H)-x(P) = 0\), d.h. \(P = H\) hat. Die stetige
Fortsetzung durch die als Grenzwert erhaltene Steigung der Tangente erlaubt das Zeichnen der
Tangente.
c) zeigt nun mit der Ordinate von \(A\) Tangentensteigungswerte bei variablem \(P\) an.
Die rote Kurve ist \(f'\) , die Ableitung von \(f\). Das in GeoGebra konstruierte Fahrrad zeigt bei
Bewegung von \(P\) an seinem Hinterrad stets die Steigung von \(f\) in \(P\) an.
|
 Zusatz 1 Zusatz 1
Radtour |
\(f(x)=\frac{1}{10}(x+2)^2(x-2)(x-4)\)
|
Interaktive Kurvendiskussion als Radtour
Alles, was üblicherweise ausgerechnet wird, kann GeoGebra angeben.
Mindestens ist das als Kontrolle hilfreich.
Mit dem CAS könnte man auch die Rechnungen prüfen. Dabei lässt man besser die Verschiebung "+2" fort, sie dient nur der Übersichtlichkeit.
 ableitung_rad.ggb
ableitung_rad.ggb 
|
 Zusatz 2 Zusatz 2
e-Funktion |
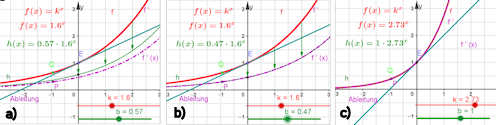 |
Die Euler'sche Zahl e ist die Basis derjenigen Exponentialfunktion,
die in \( E=(0,1)\) die Steigung 1 hat.
Aus den folgenden Überlegungen ergibt sich dann:
\( ( {\rm e}^x )'={\rm e}^x\)
 expfkt-diff.ggb
expfkt-diff.ggb  Hinführung zu dieser Erkenntnis Hinführung zu dieser Erkenntnis |
a) Erzeugung der Ableitung als Ortskurve, Vermutung, dass es sich um eine Stauchung handelt, Realisierung einer Stauchung
b) Einstellen des Stauchfaktors, so dass die Ableitung und die Stauchung zusammenfallen. Beobachtung, dass der Stauchfaktor und die Tangentensteigung in \( E=(0,1)\) übereinstimmen.
c) Einstellen der Basis, so dass Funktion und Ableitung aufeinanderfallen.
|
 Zusatz Zusatz
exponential-
Funktionen
|
Satz: Die Ableitungen der Exponentialfunktionen \(f(x)=a^x\) sind y-Achsen-Streckungen von ihr selbst. Der Streckfaktor ist die Steigung der Tangente in \( E=(0,1)\). Bei der Basis e ist er 1.
Beweis:
Der Differenzenquotient ist \( m_{sek}(x,h)=\frac{a^{x+h}-a^x}{h}=\frac{a^{h}-1}{h}\cdot a^x \). Der Bruch ist der von \(x\) unabhängige Streckfaktor, es gilt \( \lim_{h \to 0}{\frac{a^{h}-1}{h}}=m_{tangente}(0) \), (siehe Bild b)).
|
Die Euler'sche Zahl e ist per definitionem die Basis, bei der der Streckfaktor 1 ist.
|
 1.6.1.1 Ableitungsregeln 1.6.1.1 Ableitungsregeln
|
Abschnitt
1.6.1.1
Seite 54 |
\( \left( f+g \right)'=f'+g' \)
\( \left( a f \right)'=a \cdot f' \) |
\(\left( f(g)\right)' = \frac{d f}{d g} \cdot g' \) |
\( \left( u \cdot v \right)'=u'\cdot v + u\cdot v' \) |
\( \left( \frac{u}{v} \right)'=\frac{u'\cdot v - u\cdot v'}{v^2}\) |
\( \left( f^{-1}\right)'(x) =\frac{1}{f'(f^{-1}(x) )} \)
|
| Linearität |
äußere mal innere Ableitung |
Produktregel |
Quotientenregel |
Umkehrfunktion |
| \( \left( x^2+ \sin 3x\right)'=2x+3\cos 3x \) |
\( ( \sin(x^2))'=\cos(x^2)\cdot 2x \) |
\( (x^2 \sin x)'=2x\sin x+x^2\cos x \) |
\( \left( \frac{\sin x}{x^2} \right)=\frac{(\cos x) \cdot x^2-(\sin x) \cdot 2x}{x^4} \) |
\( f(x)=x^2, f'(x)=2x \leftrightarrow \left( f^{-1}(x)\right)'=(\sqrt x )'=\frac{1}{2 \sqrt x} \) |
|
 1.6.1.2 Umkehrfunktion 1.6.1.2 Umkehrfunktion
|
Abschnitt
1.6.1.2
Seite 55
Auflage 1:
Seite 54

|
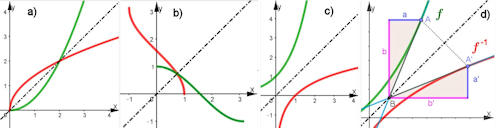
|
Abb. 1.36 Funktionen (grün)
mit Umkehrfunktionen (rot).
a) \(f(x)=\frac{1}{2} x^2 \iff f^{-1}(x)=\sqrt{2x\,}
\mbox{ für }x \geq 0\),
b) \(f(x)=\cos(x) \iff f^{-1}(x)=\arccos(x)
\mbox{ für }0\leq x \leq \pi\mbox{ bzw. } -1\leq x\leq 1\),
c) \(f(x)={\rm e}^x \iff f^{-1}(x)=\ln(x) \mbox{ für }x \in
\mathbb R\mbox{ bzw. } x\ge 0,\)
d) \(f(x)={\rm e}^x-\frac{3}{4} \iff f^{-1}(x)=
\ln(x+\frac{3}{4})\) und Erklärung für
\(f'(x)=\frac{b}{a}=\frac{1}{\frac{a'}{b'}}=\frac{1}{(f^{-1})'(y)}.\)

|
 Zusatz Zusatz
Abschnitt
1.6.1.2
Seite 54 |
 Freie Umkehrrelationen und Umkehrfunktionen, sie werden hier durch geometrische Achsenspiegelung erzeugt.
Freie Umkehrrelationen und Umkehrfunktionen, sie werden hier durch geometrische Achsenspiegelung erzeugt.
 freieUmkehrrelation.ggb
freieUmkehrrelation.ggb

Die Gleichungen der Umkehrrelationen lassen sich einfach durch Tausch von \(x\) und \(y\) schreiben.
Im Bild ist \(y=\frac{1}{4}(x+2)^4\), daher ist die Umkehrrelation \(x=\frac{1}{4}(y+2)^4\). GeoGebra zeichnet diese
implizite Gleichung sofort.
Von GeoGebra wird aber eine Parameter-Gleichung angeboten, die mehrfach Nullen als Faktoren enthält.
(Der Grund ist unklar.) Man kann sie einfach ernst nehmen, dann ergibt sich die Parameterdarstellung
\(x=\frac{1}{4}(t+2)^4\) und \(y=t\),
also die parametrisierte implizite Gleichung. Prinzipiell ist es klug, dass GeoGebra die Parameterdarstellung wählt.
|
 1.6.1.3 Elementare Funktionen und ihre Ableitungen
1.6.1.3 Elementare Funktionen und ihre Ableitungen
|
| |
\( f(x) \) |
\( f'(x) \) |
|
\( f(x) \) |
\( f'(x) \) |
|
\( f(x) \) |
\( f'(x) \) |
| (1) |
\(e^x\) |
\(e^x\) |
(5) |
\( ln x\) |
\( \frac{1}{x}\) |
(4) |
\(a^x\) |
\( ln x \cdot a^x\) |
| (2) |
\( x^a \) |
\( a x^{a-1} \) |
(5) |
\( \sqrt x \) |
\( \frac{1}{2 \sqrt x} \) |
(5) |
\( \arcsin x \) |
\( \frac{1}{\sqrt{1-x^2}} \) |
| |
\( \sin x \) |
\( \cos x \) |
(trig) |
\( \cos x \) |
\( -\sin x \) |
(trig) |
\( \tan x \) |
\( 1-\tan^2 x \) |
| |
\( \sinh x \) |
\( \cosh x \) |
(trig) |
\( \cos x \) |
\( \sinh x \) |
(5) |
Arsinh x |
\( \frac{1}{\sqrt{1+x^2}} \) |
|
| | Die mit(5) bezeichnten Funktionen sind typische
Umkehrfunktionen entsprechend der letzten Formel im Kasten 1.6.1.1. | |
 1.6.1.4 Besonderheiten der Polynome beim Ableiten 1.6.1.4 Besonderheiten der Polynome beim Ableiten
|
Abschnitt
1.6.1.4
Seite 57
Zusatz

|
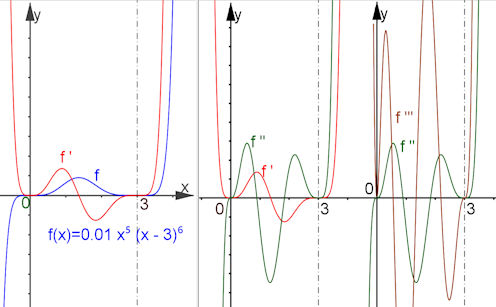
|
Zusatz zu Abschnitt 1.6.1.4 Besonderheiten der Polynome beim Ableiten
Die Vielfachheit \(k\) einer Nullstelle \(a\) sinkt bei jedem Ableitungsschritt um 1. Wenn also ein Polynom \(f\) einen
Linearfaktor \((x-a)^k \) hat, dann hat \(f'(x)\) den Linearfaktor \((x-a)^{k-1}\), entsteht dabei im Exponenten eine 1,
dann hat die entsprechende Ableitung bei \(a\) eine Nulldurchgang mit einer Steigung \(m \neq 0\). Bei weiteren Ableitungen
hat die Stelle \(x=a\) keine Besonderheit mehr.
a) Es ist in Blau \(f(x)=b\, x^5\cdot (x-3)^6 \) dargestellt. In Rot ist \(f'(x)=x^4\cdot (x-3)^5\cdot g_1(x)\) gezeigt.
Es ist \(b=0.01\). Dieser Faktor wird Folgenden den \(g_i(x)\) zugeschlagen, die hier nicht weiter bestimmt werden.
b) Es ist in Rot \(f'(x)=x^4 \cdot (x-3)^5 \cdot g_1(x)\) dargestellt. In Grün ist \(f''(x)=x^3\cdot (x-3)^4\cdot g_2(x)\) gezeigt.
c) Es ist in Grün \(f''(x)=x^3 \cdot (x-3)^4 \cdot g_2(x)\) dargestellt. In Braun ist \(f'''(x)=x^2 \cdot (x-3)^3\cdot g_3(x)\) gezeigt.
Obwohl es sich um ein Polynom 11 Grades handelt, kann man die Extremstelle \(x=\frac{15}{11}\) und die Wendestellen \(x=\frac{15}{11}\pm \frac{1}{11}\sqrt{137}\) elementar bestimmen, denn \(g_1(x)\) ist linear und \(g_2(x)\) quadratisch.
|
 1.6.2 Implizite Ableitung
1.6.2 Implizite Ableitung
|
Abschnitt
1.6.2
Seite 58
Auflage 1:
Abschnitt
1.6.2.1
Seite 57

|
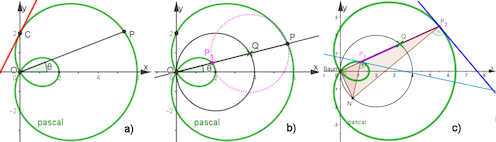
|
Abb. 1.37 Tangente an die
Pascal'sche Schnecke mit \(k=a=2\).
a) Die rote Tangente ist durch Ableiten der impliziten Gleichung
bestimmt worden (siehe Text), weiter sind Polarradius und Polarwinkel für
die Polardarstellung in Abschnitt 1.6.3.1 zu sehen.
b) zeigt darüber hinaus die Konstruktion der Pascal'schen Schnecke
als Konchoide (siehe Abschnitt 1.6.3.3), und
in c) ist eine geometrische Konstruktion der Tangente
vorgeführt, die für alle Polarkurven gilt, siehe
Abschnitt 1.6.3.2.
a) Im Buch ist die Gleichung der roten Tangente als
\(y=\frac{2a}{k}x+k\) hergeleitet.
|
| |
b) Pascal'sche Schnecken als Konchoiden, speziell als Hundekurven mit Kreisstraße.
 pascal-schnecke-koncho.ggb
pascal-schnecke-koncho.ggb  |
c) Tangenten für die Pascal'sche Schnecken kann man auch rein geometrisch erzeugen.
 pascal-schnecke-Tangenten.ggb
pascal-schnecke-Tangenten.ggb  |
 | Beweis der Tangentenkonstruktion: Im Kurvenbuch ist gezeigt, dass in dem braunen Dreieck die Seite \(\overline{ON}=r'(\theta)\) sein muss, damit die Senkrechte auf \(\overline{NP}\) Tangente in \(P\) ist. Siehe dazu hier Abb. 1.38. Dieses wird nun gezeigt: Der rechte Winkel bei \(O\) garantiert, dass \(\overline{NQ}\) Durchmesser des Wanderkreises ist. Dieser hat die Polargleichung \(r(\theta)=2a\cos{\theta}.\) Damit hat die Pascal'sche Schnecke die Polargleichung \(r(\theta)=2a\cos{\theta}\pm k\). Das hat
\(r'(\theta)=-2a\sin{\theta}\) als Ableitung der Schnecke zur Folge. Sei nun \(O'\) der diametral gegenüber \(O\) liegende Punkt des Wanderkreises. Dann ist \(ONO'Q\) ein Rechteck, bei dem \(\theta=\angle{ OO'N}\) ist, und mit \(\overline{OO'}=2a\) gilt \(\overline{ON}=2a \sin{\theta}\). q.e.d. |

|
 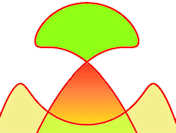 Zunächst etwas zu den Konchoiden. Man nennt sie auch Hundekurven, denn man kann sich vorstellen, ein Mensch \(Q\), nennen wir ihn Quo Vadis, wandere auf einer Straße, er habe zwei Hunde an zwei Leinen, \(P_1\), genannt Pluto strebe stets einem Baum \(O\) zu, \(P_2\), genannt Fiffi, hat Angst von dem Baum und strebt fort. Zunächst etwas zu den Konchoiden. Man nennt sie auch Hundekurven, denn man kann sich vorstellen, ein Mensch \(Q\), nennen wir ihn Quo Vadis, wandere auf einer Straße, er habe zwei Hunde an zwei Leinen, \(P_1\), genannt Pluto strebe stets einem Baum \(O\) zu, \(P_2\), genannt Fiffi, hat Angst von dem Baum und strebt fort.
Wenn die Straße eine Gerade ist, haben wir die Konchoide des Nikomedes, mit einem Kreis als Straße,
die hier vorgestellten Pascal'schen Schnecken, auch Limacon genannt, man kann \(Q\) auf jeder Kurve laufen lassen.
Das Bild zeigt eine Konchoide mit Parabel-Straße.
 Im Kurvenbuch finden Sie Geometrie und Analysis ineinander verwoben.
Im Kurvenbuch finden Sie Geometrie und Analysis ineinander verwoben.
|
 1.6.3 Ableitung bei Parameter- und Polarkurven, Teil I
1.6.3 Ableitung bei Parameter- und Polarkurven, Teil I
|
 Zusatz Zusatz
|
 |
Ellipsen zum Vergleich mit \(a=3,\;b=2\)
Violette Tangenten: Impizite Gleichung \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Blaue Tangenten: Parameter-Gleichung \(x=a\cos{t},\; y=b\sin{t}\)
Grüne Tangenten: Polar-Gleichung \(r(\theta)=\frac{p}{1-\varepsilon \cos{\theta}}\)
Zusammenhang: \(p=\frac{b^2}{a},\; \varepsilon^2=1-\frac{b^2}{a^2}\)
|
 Zusatz Zusatz |
Violett undBlau:  ellipsenTangenten.ggb
ellipsenTangenten.ggb 
|
Grün:  ellipsenTangentenPolar.ggb
ellipsenTangentenPolar.ggb 
|
Implizite Ableitung: \(\frac{2x}{a^2}+\frac{2y}{b^2}y'=0\)
also \(m_i=y'=-\frac{b^2 x}{a^2 y}\)
Punkt \(A\) auf impliziter Kurve,
Schrittweite 0.25 (bei Eig.->Algebra)
|
Parametrische Ableitung:
\(\dot{x}=-a\sin{t},\;\dot{y}=b\cos{t}\)
Tangentensteigung \(m_t=\frac{\dot{y}}{\dot{x}}=-\frac{b\cos{t}}{a\sin{t}}\)
Punkt \(B=(a \cos{t},b\sin{t})\), t mit Schieberegler
Schrittweite \(\frac{\pi}{60}\)
|
Polar-Ableitung aus \(x=r(\theta)\cos{\theta},\;y=r(\theta)\sin{\theta}\)
Tangentensteigung \(m_p=-\frac{r'(\theta)\sin{\theta}+r(\theta)\cos{\theta}} {r'(\theta)\cos{\theta}-r(\theta)\sin{\theta}}\)
Punkt \(C=(r(\theta); \theta)\) im Polaren Gitter, Achtung: Semikolon!!!!
\(\theta\) mit Schieberegler
Schrittweite \(\frac{\pi}{60}\)
|
Bei diesen drei Ellipsen werden die Tangenten auf verschiedene Art erzeugt, das führt zu dem unterschiedlichen Erscheinungsbild, aber auch zu anderem Verhalten an den Hauptscheiteln, bei denen die Tangenten parallel zur y-Achse sind. Im Einzelnen:
a) Die Tangente ist mit Tangente(A,ell) erzeugt, dieses Tool hat kein Problem an den Scheiteln. Für den wandernden Berührpunkt \(A\) sind die Pfeiltasten nacheinander von Scheitel zu Scheitel "Nord, West, Süd, Ost" verwendet. Die Autoren wissen nicht genau, wie GeoGebra die Schrittweite 0.25 umsetzt. Der Effekt ist sichtbar.
b) Die Tangente ist mit der Punkt-Steigungsform mit \(m_t\) erzeugt, bei \(t=0,\ t=\pi\) wird tatsächlich keine Tangente gezeichnet (sichtbare Lücke), der Nenner von \(m_t\) ist null.
c) Hier ist mit der genannten Formel \(m_p\) berechnet (für \(r'(\theta)\) siehe CAS-Fenster). Auch hier ist der Nenner von für \(t=0\) null. Jedoch wird für das Grafik-Fenster numerisch gerechnet, dadurch wird \(\theta=\pi\) nicht exakt getroffen und GeoGebra zeigt ein \(m_p\) von mehreren Billionen an, zeichnet aber eine (fast) Senkrechte. Ebenso geht es für \(\theta=2\pi\). Darum fehlen hier die senkrechten Tangenten nicht. |
|
 1.6.3 Ableitung bei Parameter- und Polarkurven, Teil II
1.6.3 Ableitung bei Parameter- und Polarkurven, Teil II
|
Abschnitt
1.6.3.2
Seite 60
Auflage 1:
Seite 59

|
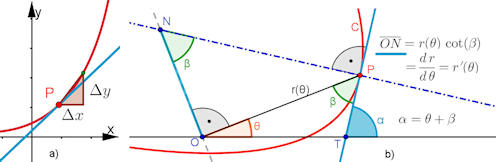
|
Abb. 1.38 Steigung und Tangente. a)
Sekantensteigung und Tangente für die
explizite kartesische Darstellung, b) Tangente und Normale
für Polarkurven.

 Auf der Kurven-Website sind die Formeln zusammengetragen. Vollständig bewiesen sind sie im zugehörigen Kurvenbuch S. 318f. Auf der Kurven-Website sind die Formeln zusammengetragen. Vollständig bewiesen sind sie im zugehörigen Kurvenbuch S. 318f.
Die hier links gezeigte geometrische Konstruktion der Tangente ist in Abb. 1.37 c) bei den Pascal'schen Schnecken angewendet und dort im Zusatz bewiesen.
Rechnerisch und grafisch ist die polare Ableitung soeben im Zusatz zu den Ellipsen-Tangenten vorgeführt.
|
 1.7 Funktionen untersuchen Weiter mit 1.8.
1.7 Funktionen untersuchen Weiter mit 1.8.
|
|
|
 1.7.1 Lokale Extremstellen
1.7.1 Lokale Extremstellen
|
Abschnitt
1.7.1
Seite 62
Auflage 1:
Seite 61

|
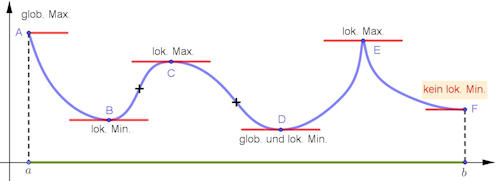
|
Abb. 1.39 Lokale versus globale
Extrema. Für jeden der Punkte \(A\) bis \(F\) ist angegeben, um welche
Art von Extremum es sich handelt. In jedem Punkt ist eine Parallele
zur x-Achse gezeichnet, die die Extremaleigenschaft verdeutlicht,
sie ist in \(A\) und \(E\) nicht Tangente.
Die schwarzen Kreuze bezeichnen Wendepunkte, die in Abschnitt
1.7.4 besprochen werden.
 ExtremumLokalGlobal.ggb
ExtremumLokalGlobal.ggb
|
 Zusatz Zusatz |
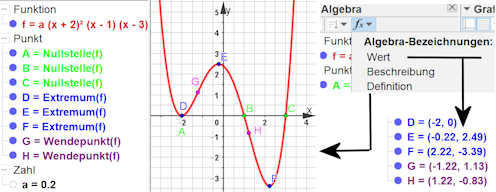
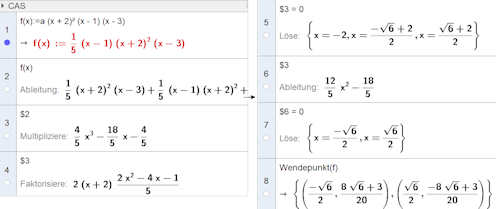
 kurvendiskussion.ggb
kurvendiskussion.ggb 
|
Kurvendiskussion
Hier auf der Webseite haben wir - im Gegensatz zum Buch - den Platz, Ihnen eine übliche Kurvendiskussion vorzustellen und Ihnen die Unterstützung durch GeoGebra zu zeigen. Wir gliedern in die Teile 1.) und 2.). Im 7. Kapitel werden wir vor allem auf die kniffligeren Vorgehensweisen eingehen.
Als Start öffen Sie das CAS-Fenster und definieren Sie die Funktion, die Sie untersuchen wollen, mit f(x):=.... Nur im CAS ist der Doppelpunkt nötig.
Durch dieses Vorgehen haben Sie dann dieses auch im Algebrafenster. Andersherum hätten Sie zwei verschiedene Namen.
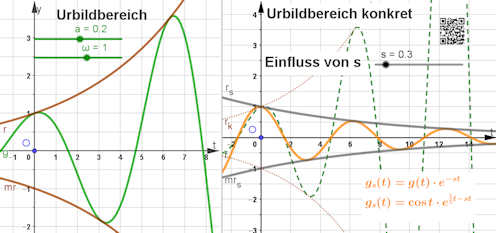
1.) Elementare Erkundung
mit dem Algebra- und dem Grafikfenster. Legen Sie \(a=0.2\) fest. So haben Sie später nun eine Steuerung für den Platzbedarf. Wie man solche "Form"-Parameter in CAS bewahrt, finden Sie hier.
Nun ist \(f\) im Algebrafenster bekannt und der Graph erscheint im Grafikfenster.
Wie Sie links sehen, braucht man nur die üblichen Ziele der Kurvendiskussion zu nennen, um sofort die entsprechenden Punkte auf dem Graphen zu bekommen. Deren Koordinanten erhält man, indem im rechten Pulldownmenu des Algebrafensters "Wert" wählt.
2.Symbolische Berechnung mit CAS: Es gibt das CAS-Menu
 . .
Seine Befehle werden auf den Ausdruck angewandt, der am Anfang einer CAS-Zeile steht. Z.B. steht in Zeile 3 $2 (für Zeile 2), geklickt wurde der Button mit den Klammern, das hat die Klammern in Zeile 2 (hier sind nicht alle zu sehen) aufgelöst und alles nach Potenzen von x zusammengefasst.
Aber es sind auch Befehle möglich, wie Zeile 8 zeigt.
|
 1.7.2 Oszillierende Funktionen, Sinus-Wunderdinge
1.7.2 Oszillierende Funktionen, Sinus-Wunderdinge
|
Abschnitt
1.7.2
Seite 64
Auflage 1:
Seite 63

|
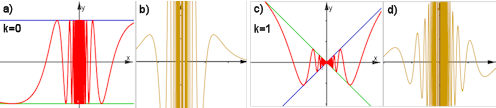
|
Abb. 1.40 Sinus-Wunderdinge:
\(f_k(x)=x^k\sin{\frac{1}{x}}\) und \(f_k(0):=0\)
a) Graph von \(f_0\) und b) Graph von \(f_0'\).\(\qquad\)
c) Graph von \(f_1\) und d) Graph von \(f_1'\).
\(f_0\) ist unstetig, \(f_1\) ist stetig, beide Ableitungen sind nicht
beschränkt.
Für alle vier Bilder:
 sinwunder-xksin1durchx.ggb
sinwunder-xksin1durchx.ggb 
|
Abschnitt
1.7.2
Seite 64
Auflage 1:
Seite 63

|
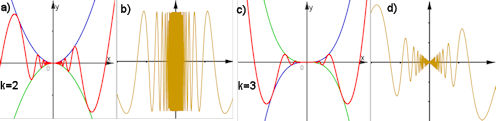 
|
Abb. 1.41 Sinus-Wunderdinge:
\(f_k(x)=x^k\sin{\frac{1}{x}}\) und \(f_k(0):=0\)}
a) Graph von \(f_2\) und b) Graph von \(f_2'\).\(\qquad\)
c) Graph von \(f_3\) und d) Graph von \(f_3'\).
\(f_2\) ist differenzierbar, \(f_2'\) zwar beschränkt, aber in 0 nicht stetig.
\(f_3\) ist stetig differenzierbar.
|
Abschnitt
1.7.2.1
Seite 66
Auflage 1:
Seite 65

|
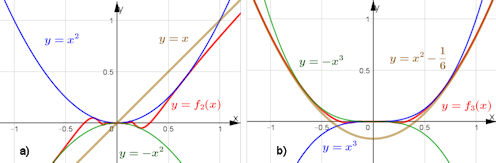
|
Abb. 1.42 Asymptoten für
\(f_k(x)=x^k\sin \frac{1}{x}\). a)
Graphen von \(f_2,\ y=\pm x^2,\ y=x\),
b) Graphen von \(f_3,\ y=\pm x^3,\ y=x^2-\frac{1}{6}\). Gezeigt sind
also jeweils die oszillierende Kurve (rot),
die einhüllenden Potenzfunktionen (blau und grün) und die Asymptote
(ockerfarben).
 sinwunderAsymptoten.ggb
sinwunderAsymptoten.ggb (ohne Einhüllende) (ohne Einhüllende)
 xksin1durchxAsymptote.ggb
xksin1durchxAsymptote.ggb 
|
 1.7.3 Krümmungen
1.7.3 Krümmungen
|
Abschnitt
1.7.3.1
Seite 67
Auflage 1:
Seite 66

|
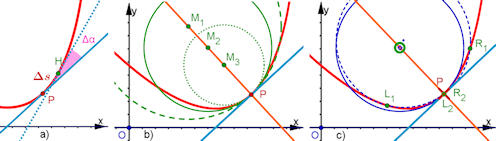
|
Abb. 1.43 a) Krümmung als Grenzwert von
\(\frac{\Delta \alpha}{\Delta s}\),
b) Krümmungskreis interaktiv mit der Normalen finden: Ziehe an den Mittelpunkten, welcher Kreis ist der intuitiv beste Krümmungskreis?
c) Krümmungskreis interaktiv als Kreis durch drei Kurvenpunkte
finden (Schupp und Henn). Rücke einen linken Punkt L und einen rechten Punkt R (fast) auf P.
Der "Grenzkreis" müsste der Krünmmmungskreis sein.
 kruemmungErkunden.ggb
kruemmungErkunden.ggb 
|
 1.7.4 Wendepunkte
1.7.4 Wendepunkte
|
 Zusatz Zusatz
Zu
Abschnitt
1.7.4
Seite 70
Auflage 1:
Seite 69

|
|
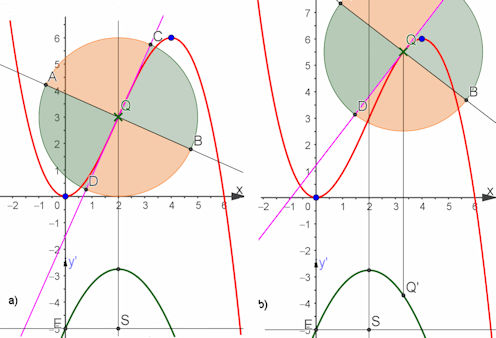
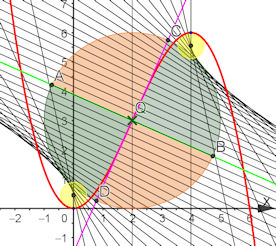
Abb. Z-70 Zusammenhang zwischen Wendepunkten, Wendetangenten und Krümmumg
Es geht hier als Beispiel um die Funktion \(f(x)=\frac{3}{16}x^2(6-x)\).
Eine Wendestelle der Ausgangskurve (rot) ist dort, wo die Ableitung \(f'(x)=-\frac{9}{16} x(x-4)\),
in Grün tiefer gezeichnet, ein Extremum hat. O.B.d.A. sei dieses, wie links, ein Maximum.
Die Ordinate dieses Maximums gibt die Wendesteigung \(m_w=\frac{9}{4}\) an.
In einer hinreichend kleinen Umgebung ist links und rechts davon die Kurvenssteigung also geringer.
In a) ist die Wendetangente violett dargestellt, der durch Wendetangente und Normale geviertelte Kreis um den Wendepunkt \(Q\) zeigt deutlich, dass die rote Kurve nur in den gegenüberliegenden grünen Kreisvierteln verläuft.
Die Kurve, der Funktionsgraph, durchsetzt also die Wendetangente.
In b) ist \(Q\) nicht der Wendepunkt und die violette Gerade ist nur eine "gewöhnliche" Tangente in \(Q\).
Sie verläuft in zwei benachbarten, verschienden farbigen Kreisvierteln.
Im unteren Bild sind in Schwarz einige Normalen in wanderndem
\(Q\) gezeichnet.
Auf ihnen liegen die Mittelpunkte der Krümmungskreise.
Diese sind hier nur für die beiden Extrema gezeichnet und berechnet nach der Formel 11.20 im Buch [\cite{HaftendornK}{Kurven}]
\(M_1=(0,n)\) und \(M_2(4,6-n)\) mit \(n=f(0)+\frac{1}{f''(0}(1+(f'(0))^2)=\frac{4}{9}\).
Die Wendetangente kann als Rand des Krümmungskreises mit Radius \(\infty\) aufgefasst werden.
Die beiden Nachbarn der grünen Normalen durch \(Q\) sind fast parallel zu ihr. Die Hüllhurve der
Normalen heißt Evolute der Kurve, hier nur für \(Q\) zwischen den Extrema dargestellt.
Wendepunkte+Normalen.ggb |
 1.8 Integralrechnung Weiter mit 1.9.
1.8 Integralrechnung Weiter mit 1.9.
|
|
|
|
|
 1.8.1 Riemannsche Ober- und Untersummen 1.8.1 Riemannsche Ober- und Untersummen
|
Abschnitt
1.8.1
Seite 71
 |
|
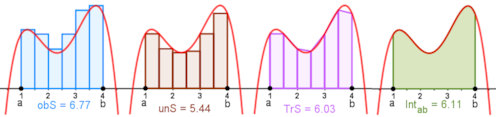
Abb. 1.44 Integral und Riemann’sche Summen.
Obersummen in Blau wählen die maximale Ordinate im Teilintervall,
Untersummen in Braun die minimale Ordinate,
Trapezsummen in Violett
sind eigentlich keine Riemann’schen Summen, verbessern aber die numerische Näherung, Sie sind auch die Mittelwerte aus Unter- und Obersummen,
bei
Erhöhung der Balkenanzahl streben alle gegen das
Integral, die grüne Fläche.
 intdef.ggb
intdef.ggb 
 int-einf-parabel-rechts.ggb, Einführung bei Parabel
int-einf-parabel-rechts.ggb, Einführung bei Parabel 
|
 1.8.2 Hauptsatz der Differential- und Integralrechnung
1.8.2 Hauptsatz der Differential- und Integralrechnung
|
Abschnitt
1.8.2.1
Seite 73

|

|
Abb. 1.45 Teppichabrollen -
Integralfunktion. a) und c) Ein auf eine Stange
gewickelter Teppich mit einer Funktion als oberem Rand
wird von \(A\) an bis \(B=(x,0)\) abgerollt. In c) ist mit der roten Kurve
gezeigt, welche Teppichfläche an jeder Stelle \(x\) zu sehen war.
b) und d)
Auch wenn die Randkurve sinkt, wächst die sichtbare Teppichfläche weiter,
solange die Randkurve positiv ist.
Die Funktion, die die abgerollte Teppichfläche angibt, hat den Namen
Integralfunktion, siehe unten.
 teppichabrollen.ggb
teppichabrollen.ggb 
|
Abschnitt
1.8.2.2
Seite 73

|
|
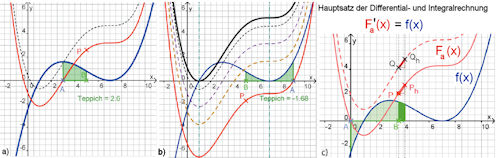
Abb. 1.46 Hauptsatz
der Differential- und Integralrechnung. a) und b) zeigen
Integralfunktionen zu der (blauen) Funktion \(f\), wie im Text beschrieben.
c) Zeigt, dass der Flächenzuwachs
beim Ziehen von \(B=(x,0)\) auf \((x+h,0)\) für alle Integralfunktionen gleich
ist, denn er hängt offensichtlich von der Stellung von \(A\) gar nicht ab.
Denkt man diesen Zuwachs infinitesimal, heißt das, dass
alle Integralfunktionen an einer gegebenen Stelle
\(x\) dieselbe Zuwachsrate, also dieselbe Steigung haben und dass
diese Steigung von der Ordinate \(f(x)\) angegeben wird.
1.) zu a) und c) teppichzuwachs+Stammfkt.ggb
teppichzuwachs+Stammfkt.ggb 
2.) c) allein teppichzuwachs-pur.ggb
teppichzuwachs-pur.ggb  |
| |
3.) b) und CAS  teppich-integralfkt.ggb
teppich-integralfkt.ggb  Anmerkung: In dieser Datei werden Integralfunktionen mit GeoGebra-CAS bestimmt. Es wird deutlich, dass nicht alle Stammfunktionen von f als Integralfunktionen auftreten können, aber alle Integralfunktionen sind auch Stammfunktionen. Auch die in Abb. c) für den Zuwachs gezeichnete Stammfunktion tritt bei den Integralfunktionen nicht auf. Sie ist der Deutlichkeit halber gewählt.
Anmerkung: In dieser Datei werden Integralfunktionen mit GeoGebra-CAS bestimmt. Es wird deutlich, dass nicht alle Stammfunktionen von f als Integralfunktionen auftreten können, aber alle Integralfunktionen sind auch Stammfunktionen. Auch die in Abb. c) für den Zuwachs gezeichnete Stammfunktion tritt bei den Integralfunktionen nicht auf. Sie ist der Deutlichkeit halber gewählt. |
 1.8.3 Wichtige Eigenschaften des bestimmten Integrals
1.8.3 Wichtige Eigenschaften des bestimmten Integrals
|
Abschnitt
1.8.3.1
Seite 75

|
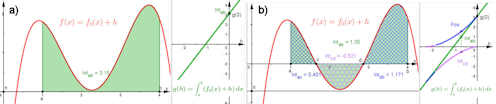
|
Abb. 1.47 Das Integral als Flächenbilanz.
a) Für \(h=0\), also \(f(x) = f_0(x)\ge 0\) ist das Integral die
Fläche (grün) unter
\(f\) bis zur x-Achse. Rechts in a) ist gezeigt, dass bei gleichmäßiger
Verringerung der Verschiebung \(h\) der Integralwert linear
sinkt (grüne Gerade).
b) Zeigt eine Stellung von \(h\) mit sowohl positiven als auch negativen
Werten von \(f\), das Integral ist eine Flächenbilanz. Rechts sind der
positive (blau) und der negative Anteil (violett) des Integrals in
Abhängigkeit von \(h\) dargestellt. Die Bilanz (grün)
aber ändert sich wieder linear.
 int-flaeche.ggb
int-flaeche.ggb 
 int-fl-bilanz.ggb
int-fl-bilanz.ggb 
|
Abschnitt
1.8.3.2
Seite 76

|

|
Abb. 1.48 Das Integral und Zerlegungen des
Integrationsintervalls.
a) setzt die Bewegung aus Abb. 1.47 fort. Dabei
zeigt sich, dass die Festsetzung \(\int_d^b{f(x){\rm d} x=0}\) für \(d=b\) sinnvoll ist.
Bei weiterem Absinken von \(h\) würde das Integral wieder die Flächenbedeutung,
aber negativ, erhalten. b) zeigt das Zerlegungsgesetz:
es ist dargestellt, dass es unabhängig von der Lage von \(c\) gilt,
vorausgesetzt, das Integral über das jeweilige Gesamtintervall existiert.
|
| |
a)  int-fl-bilanz.ggb
int-fl-bilanz.ggb  (Datei wie für Abb. 1.47 b)) (Datei wie für Abb. 1.47 b))
b)  int-zerlegung.ggb
int-zerlegung.ggb  Beachten Sie, dass die Kennzeichnung negativ abhängig von der Stellung von c genau richtig erscheint. Siehe GeoGebra->Bedingungen
Beachten Sie, dass die Kennzeichnung negativ abhängig von der Stellung von c genau richtig erscheint. Siehe GeoGebra->Bedingungen
|
Abschnitt
1.8.3.3
Seite 77

|
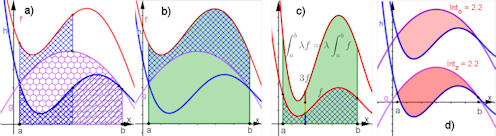
|
Abb. 1.49 Integral-Gesetze.
a) \(f=g+h\), die
blau karierte Integralfläche unter \(h\) wird über \(g\) versetzt "gemalt".
b) Die Integralfläche von \(f\), der Summe, ist dann die Summe der
Flächen zu \(g\) und \(h\).
c) Die Integralfläche von \((3 f)\) (grün) ist
das 3-fache der Integralfläche von \(f\) (blau kariert).
d) Haben \(f\)
und \(g\) höchstens an den Intervallgrenzen gemeinsame Ordinaten, dann ist der
Flächeninhalt zwischen beiden Graphen unabhängig von einer gemeinsamen
Verschiebung in y-Richtung und damit auch von der Lage der Graphen relativ zur
x-Achse, siehe Satz 1.9.
a) und b)
 Integral-linear-Summe.ggb
Integral-linear-Summe.ggb 
c) und d)
 Integral-linear-lambda.ggb, Vielfache und Zwischenflächen
Integral-linear-lambda.ggb, Vielfache und Zwischenflächen 
|
|
Anregung 1.3
Abschnitt
1.8.3.4
Seite 78

|
|
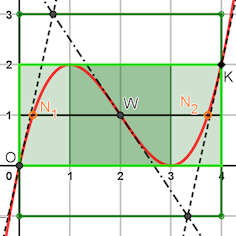 |
1.3 Erkundung der Polynome 3. Grades
Abb. 1.50 Polynome 3. Grades im Affenkasten
Betrachten Sie das Polynom \(p(x)=\frac{1}{2}x(x-3)^2\).
Die Extrema von \(p\) definieren in der gezeigten Art einen dunkelgrünen Kasten
mit vier Zellen, der in Hellgrün auf 8 Zellen erweitert ist. Im Zentrum
ist der Wendepunkt \(W\).
Weisen Sie nach, dass die Kastenecke \(K\) ein
Kurvenpunkt ist.
Die Betrachtung der Flächen -- z.B. zwischen \(y{=}1\) von
\(N_1\) bis \(W\) oder zwischen x-Achse und Kurve von \(O\) bis Minimumstelle, u.a. --
bietet einige Besonderheiten, viele Flächenverhältnisse sind rational.
|
Hinweis
Jedes Polynom 3. Grades hat genau einen Wendepunkt \(W\).
Ein beliebiger Kurvenpunkt \(P\) definiert mit seiner Tangente,
der zu ihr parallelen Geraden durch \(W\) und den Senkrechten durch \(P\)und \(W\) eine
Parallelogramm-Zelle.
Acht solche Zellen mit \(W\) im Zentrum bilden einen
schrägen Affenkasten mit allen oben angesprochenen Eigenschaften.
Der Name ist gewählt, weil jedes Polynom 3. Grades
in jeden solchen Kasten gesperrt werden kann. Der Kasten im
Bild ist nur ein Sonderfall.
Mittelalterliche Gaukler präsentierten auf Märkten ihre Affen in Kästen.
In Abb. 1.50 lohnt sich auch der Vergleich mit den
Kastenzellen. Diese haben hier die Fläche \(Z=1\), im Allgemeinen:
\(Z=(x_W-x_{max})(y_{max}-y_W)\).
Wendetangente und Randtangenten schneiden sich auf den
Kanten eines doppelt so hohen Kastens, mit ihnen ergeben sich
weitere besondere Flächen.
Jedes Polynom 3. Grades mit Extrema hat so einen Kasten mit diesen Eigenschaften.
|
|
|
Anregung 1.4
Abschnitt
1.8.3.4
Seite 79

|
|
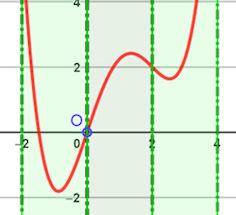 |
1.4 Erkundung der Polynome 4. Grades
Abb. 1.51 Polynome 3. Grades im Patherkäfig
Es geht beispielhaft um \(p(x)=\frac{1}{4} x^4 -x^3 + 3x\).
Die Wendepunkte definieren einen „Pantherkäfig“ mit vier Stangen,
d.h. senkrechten Geraden, in gleichem Abstand. Lesen Sie das Gedicht von
Rainer Maria Rilke: "`Der Panther".
|
Aufgaben
- Zeigen Sie, dass die Schnittpunkte der Wendetangenten mit der Kurve ebenfalls
auf diesen Stangen liegen.
- Betrachten Sie die beiden Flächen, die sich jeweils zwischen
Wendetangente und Kurve bilden.
- Zeigen Sie, dass die Geraden durch einen Wendepunkt und den nächstgelegenen
Schnittpunkt aus Aufgabe 1. die in Aufgabe 2. genannten Flächen halbieren.
- Bilden Sie mit \(g(x)= -x\) das Polynom \(q(x)=p(x)+g(x)\) und
erkunden Sie es auf gleiche Weise.
Hinweis: Die Addition einer Geraden mit
der Nullstelle \(x_0\) zu einer Funktion bewirkt
immer eine Scherung mit der Scherachse \(x=x_0\).
Scherungen sind flächentreu.
In diesem Buch finden Sie Scherungen in Abb. 2.44 und
am Ende des Abschnitts 2.5.3.2.
- Zeigen Sie, dass die Geraden durch einen Wendepunkt und den
nächstgelegenen Schnittpunkt aus Aufgabe 1.
die in Aufgabe 2. genannten Flächen halbieren.
- Warum erhalten solche Scherungen von Funktionen immer Wendestellen?
Warum erklärt dies die Beobachtungen in Aufgabe 2.?
- Machen Sie sich klar, dass alle diese Besonderheiten für jedes Polynom 4. Grades,
das überhaupt mehrere Extrema hat, gelten.
- Erkunden Sie in der vorigen Anregung 1.3
auch für Polynome 3. Grades, was die
Addition einer Geraden bewirkt.
Betrachten Sie die beiden Flächen, die sich jeweils zwischen
Wendetangente und Kurve bilden.
Hinweis
Beachten Sie, dass der Grund für diese Zusammenhänge darin
liegt, dass Polynome 4. Grades mit mehreren Extrema immer
als zweite Ableitung eine Parabel mit zwei verschieden Nullstellen haben müssen.
|
|
| |
Anregung 1.5
Abschnitt 1.8.3.4
Seite 80

|
|
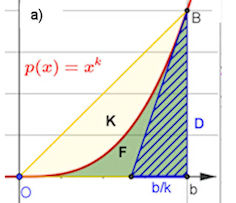
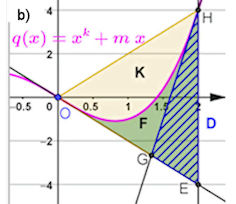
|
1.5 Erkundung besonderer Flächen bei Potenzfunktionen
Abb. 1.52 Zu a): Das Segment K ist begrenzt von der Potenzfunktion
mit Exponent
\(k,\; k>1\), und der Strecke
\(\overline{OB}\),
die Fläche F wird gebildet von der Potenzfunktion,
ihrer Tangente in \(B\) und der x-Achse.
Zeigen Sie, dass gilt:
\(\frac{K}{F}=\frac{k}{1}\).
Zu b): Wie verhält es sich in dieser neuen gescherten Konstellation?
|
|
|
Anregung 1.6
Abschnitt 1.8.3.4
Seite 80

|
|
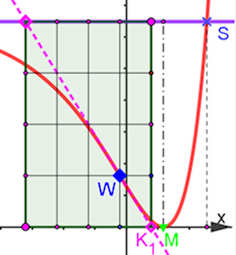 |
1.6 Erkundung des Eulerkastens
Abb. 1.53 Der Eulerkasten von \(f(x)=({\rm e}^x-k)^2\)
Bei dieser Funktion lohnt es sich besonders, die Gestalt des Graphen durch
Abwärtsschieben der e-Funktion und Quadrieren zu verstehen.
Die Flächen, die im
Folgenden betrachtet werden und die Sie mit Integralen berechnen können,
befinden sich alle zwischen der Asymptote und dem Graphen von \(f\), der roten Kurve.
Sei \(Z\) die Fläche einer der 16 gleichen Kastenzellen. Erstaunlicherweise lassen
sich viele der Flächen als ganzzahlige Vielfache von \(Z\) oder
\(\frac{1}{2}Z\) ausdrücken.
|
Aufgaben
- Die Wendetangente schneidet aus dem Streifen zwischen x-Achse und
Asymptote einen Kasten der von \(k\) unabhängigen Breite 2 heraus. \(W\) ist der
Wendepunkt dieser Euler'schen Funktion, er definiert die rechte untere Zelle, daher der Name
Eulerkasten oder Wendekasten.
- Die links unbegrenzte Fläche zwischen Kurve und Asymptote
(kurz FzKuA) ist genau so groß wie die Fläche das Eulerkastens, also \(16\);
Wir greifen mit dieser Fragestellung etwas vor, Sie erfahren die notwendige
Vorgehensweise für "`uneigentliche"' Integrale im
Abschnitt 1.8.11
- Die links unbegrenzte FzKuA, die rechts von der Senkrechten an der
Wendestelle begrenzt wird, ist \(7\;Z\).
- Die links unbegrenzte FzKuA, die rechts von der Wendetangente begrenzt
wird, ist \(\frac{5}{2} Z\).
- Die FzKuA zwischen Wendestelle und Nullstelle \(M\) ist \(5\;Z\).
- Die FzKuA zwischen Nullstelle und Schnittpunkt \(S\) ist \(4 Z\)
- Die links unbegrenzte FzKuA ab der linken Kastengrenze ist
inkommensurabel (lat. nicht gemeinsam messbar)
mit \(Z\), d.h. sie ist kein rationales Vielfaches von \(Z\).
Das zeigt, dass die anderen Ergebnisse etwas Besonderes sind.
|
|
|
|
 1.8.4 Partielle Integration und Substitution
1.8.4 Partielle Integration und Substitution
|
Abschnitt
1.8.4
Seite 81
Auflage 1:
Seite 77
|
 Zur partiellen Integration haben wir (noch) keine Bilder. Das hängt auch mit dem nachfolgend beschriebenen Problem des Variablengebrauchs zusammen. Zur partiellen Integration haben wir (noch) keine Bilder. Das hängt auch mit dem nachfolgend beschriebenen Problem des Variablengebrauchs zusammen.
Bei Bildern zur Substitution ist es ein grundsätzliches Problem, dass in GeoGebra die freie Variable stets \(x\) heißen muss, man aber bei Substitutionen in \(g(x)\) einen Termteil \(u(x)\) nennt und dann mit \(x=f(u)\) die Funktion \(f(u)\) einführt. Dadurch wird g statt von \(x\) von \(u\) abhängig, handschriftlich drückt man dies durch \(g(u)\) aus und das bedeutet hier NICHT, wie meist üblich, dass für \(x\) einfach \(u\) geschrieben wird, sondern wir definieren eine neue Funktion
\(h(u)=g(f(u)\)
In den folgenden Beispielen sind im rechten Grafikfenster konsequent die Funktionen mit \(u\) geschrieben, obwohl sie in Algebrafenster ausschließlich \(x\) als Argumente haben.
In den Legenden der Beispiele können wir das besser herausarbeiten.
Die ersten beiden Beispiele sind rechnerisch im Buch vollständig durchgeführt. Lediglich die Bilder sind nun zusätzlich.
|
 Abschnitt Abschnitt
1.8.4
Seite 82
Auflage 1:
Seite 79
Abb. S79Z1 |
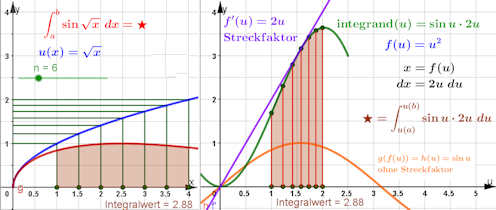 |
TYP 1: "Ein Termteil wird ersetzt."
Substitution für \( \int_a^b{\sin{\sqrt{x}}\ {\rm d}x} \).
 substi-sinwurzelx.ggb
substi-sinwurzelx.ggb
Vorgehensweise: Teil 1: Man entscheidet, welchen Term man substituieren möchte, definiert und zeichnet \(u(x)\). Zu einer äquidistanten Punktfolge zwischen den Grenzen \(a,\ b\) zeichnet man die Folge der Ordinaten der entsprechenden Punkte auf dem Graphen von \(u\) und erhält dadurch eine Punktfolge auf der y-Achse. Diese wird im zweiten Fenster als Folge \(u(a),u(x_1), \dots, u(b)\)
eingetragen.
|
 |
Teil 2: Nun definiert man, i.d.R. nach Umformung, \(x=f(u)\) und bestimmt die Ableitung \(f'(u)\). Im Algebrafenster und für die Zeichnung des violetten Graphen von \(f'\) muss man das Argument \(x\) nennen, aber im CAS kann man wirklich \(u\) nehmen.
Teil 3: Das rechte Grafikfenster braucht nun die, i.d.R. einfachere, Funktion \(h(u)=g(f(u)\), zum Zeichnen wieder mit \(x\) geschrieben. Nun kann man die Punktfolge \((u(x_i),g(u(x_i))\cdot f'(u(x_i))\) bilden und auch den grünen Graphen \({\rm integrand}(u)=h(u)\cdot f'(u)\) bilden und mit Argument \(x\) zeichnen.
Teil 4: Es können jetzt die Intergrationsbefehle verwendet werden: Im linken Fenster für den ursprünglichen Integranden \(g(x)\) (rot) und im rechten Fenster für den in Teil 3 definierten Integranden.
Anmerkung: Die gleichmäßigen Riemann'schen Trapez-Balken links werden rechts transformiert in Riemann'sche Trapez-Balken (annähernd) gleicher Fläche. Der Integralwert, für den den Balkenbreite gegen null strebt, ist daher derselbe.
Den ursprünglichen Integranden \(g(x)\) können Sie beliebig ändern, zum Beispiel  substi-coswurzelx.ggb
substi-coswurzelx.ggb . . |
 Abschnitt Abschnitt
1.8.4
Seite 82
Auflage 1:
Seite 79
Abb. S79Z2
|
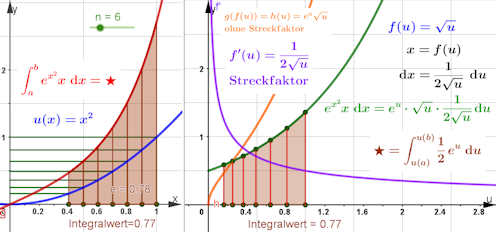 |
TYP 2: "Die Ableitung erscheint."
Substitution für \( \int_a^b{e^{x^2}x \ {\rm d}x} \).
Wir behandeln diesen Fall mit der Standardmethode, wie sie im vorigen Beispiel durchgeführt ist. Hat man mit der Integrierung durch Substitution Erfahrung, so geht man wie im Buch beschrieben vor und "sieht" x als wesentlichen Bestandteil der Ableitung der naheliegenden Substitution \(u=u(x)=x^2\), was sofort zu \({\rm d}u=2x{\rm d}x\) führt. Man schreibt um:
\(\int_a^b {\rm e}^{x^2}x\ {\rm d}x=\)
\(\int_{u(a)}^{u(b)}{\rm e}^{u}\frac{1}{2}\ {\rm d}u={\rm e}^x |_{a^2}^{b^2}\).
 substi-ex2x.ggb
substi-ex2x.ggb
|
 Abschnitt Abschnitt
1.8.4
Seite 82
Auflage 1:
Seite 79
Abb. S79Z3
|
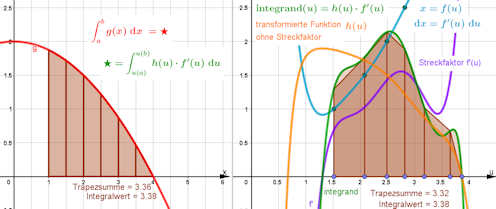 Freier TYP 1: Die Transformation \(x=f(u)\) wird frei gewählt.
Freier TYP 1: Die Transformation \(x=f(u)\) wird frei gewählt.
Substitution von \(x\) in \( \int_a^b{(2-\frac{x^2}{8})\ {\rm d}x} \) mit einem beliebigen Polynom.
 Substitution-freie-Transformation.ggb
Substitution-freie-Transformation.ggb 
Wir wollen auch eine Geogebra-Datei bereitstellen, in der die Substitution nicht fest vorgegeben ist. Die freie Eingabe einer Substitutionsfunktion \(u(x)\) ist aber problematisch, da schwer zu kontrollieren ist, wo das vorgegebene Integrationsinterval "landet" und damit d
er Bereich für die Graphik 2 schwer zu bestimmen ist. Deshalb können Sie hier die Funktion \(u(x)\) dadurch festlegen, dass Sie im zweiten Graphikfenster die Funktionswerte \(u(1),\ u(1.5),\ \dots, u(4)\) durch Ziehen der sechs blauen Punkte auf der \(u\)-Achse festlegen. Dann wird \(u(x)\) geeignet interpoliert. Da in Graphik 2 vor allem die Umkehrfunktion \(f(u)\) gebraucht wird, wird diese durch ein (Lagrange-)Polynom interpoliert.
Es ist, wie auch in den anderen Beispielen, \(h(u)=g(f(u))\).
Achten Sie beim Verschieben der Punkte darauf, dass \(u(x)\) monoton wachsend bleibt, sonst gibt es ein unübersichtliches Durcheinander im Bild, obwohl die Rechnung weiterhin funktioniert. Und: ziehen Sie vorsichtig, denn vor allem der Streckfaktor \(f'(u)\) reagiert sehr empfindlich auf die Lage der Punkte!
Die Funktion \(g(x)\) hingegen können Sie gerne ändern.
|
 Abschnitt Abschnitt
1.8.4
Seite 82
Auflage 1:
Seite 79
Abb. S79Z4
|
|
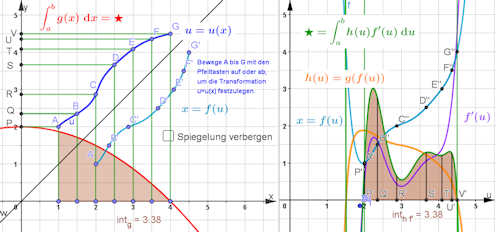
Freier TYP 2: Die Substitution \(u=u(x)\) wird frei gewählt.
Um die vorige Transformation besser zu verstehen, wird hier eine Funktion \(u=u(x)\) frei gewählt, die dann auf dieselbe Art, wie in Abb. S79Z1 und S79Z2 zu einer Transformation mit einem Polynom \(x=f(u)\) führt.
Wie schon in der vorigen Legende gesagt, braucht man eine Funktion \(f\), die man ableiten kann.
Darum gehen wir hier folgendermaßen vor:
Die \(u\) definierenden Punkte A bis G können auf einer gleichabständigen Parallelenschar mit den Pfeiltasten (mit feiner Schrittweite von 0.001) beliebig eingestellt werden. \(u\) sollte möglichst monoton werden. Auch ist es schöner, wenn \(u\) wirklich eine Funktion und nicht nur eine Relation wird, siehe unten. Die Funktion \(g(x)\) können Sie auch hier ändern.
 substi-frei-vari.ggb
substi-frei-vari.ggb 
|
Durch geometrische Spiegelung an der Winkelhalbierenden entstehen die Punkte einer Umkehrrelation, die man durch ein Interpolationspolynom \(f\) verbindet. Eingeschänkt auf den relevanten Bereich spiegelt man diese
zurück. Dadurch erhält man \(u\) i.d.R. nicht als Funktion, sondern als Relation, die als Parameterkurve dargestellt wird. Das ändert aber nichts an der Richtigkeit der Substitutionsregel, für die nur \(x = f(u)\) eine Funktion sein muss.
Nun nimmt man die Ordinaten der Punkte A bis G als
Abszissen auf der u-Achse im rechten Grafikfenster und geht dann weiter so vor wie bei den obigen Beispielen. Nur im vorigen Beispiel ist - wie hier - \(x=f(u)\) (hellblau) mit den transformierten definierenden Punkten gezeigt.
Man bildet also aus \(f'(u)\) (violett, alle Funktionen in GeoGebra mit x geschrieben) und \(h(u)=g(f(u))\) (orange) ein Produkt (grün) und integriert es.
Es zeigt sich hier, dass für jede Transformation die beiden mit "Stern" gekennzeichneten Integrale übereinstimmen.
|
 1.8.5 Flächenfragen in der Darstellungsvielfalt
1.8.5 Flächenfragen in der Darstellungsvielfalt
|
Abschnitt 1.8.5
Seite 83
|
Alle bisherigen Abschnitte in der Integralrechnung haben
sich den Eigenschaften des Integralbegriffs und dem Bewältigen der
Integration gewidmet. Dies alles wurde für die expliziten
kartesischen Funktionen notiert. Es gibt aber eine Vielfalt von
Darstellungsarten, die wir in Abschnitt 1.5 vorgestellt
haben.
Bei den impliziten kartesischen Kurven
kommt man für
Flächenbetrachtungen nur weiter, wenn man die Kurven \textbf{parametrisiert}.
Das heißt man sucht eine Größe \(t\) die geeignet ist, nacheinander in einem
"`Durchlauf"' alle Punkte mit \( x(t)\) und \(y(t)\) zu erfassen. Alternativ gelingt
evt. eine Darstellung in Polarkoordinaten. Vielversprechend sind auch
geometrische Methoden, da die algebraischen Kurven i.d.R. eine oder sogar
mehrere geometrische Konstruktionsmöglichkeiten haben.
Die Parameterdarstellung umfasst die explizit kartesische, also
sollte das im nächsten Abschnitt behandelte Flächenkonzept alles Bisherige
als Sonderfall beinhalten. Für die dann folgenden Polarkurven muss
für die dort betrachteten Sektorflächen dasselbe herauskommen, wie bei der
Auffassung der Polarkurve als Parameterkurve. Wir vertrauen darauf, dass
diese vielfältige Sichtweise Ihre mathematische Kompetenz und damit auch
ihre Handlungsfreiheit fördert.
|
 1.8.6 Flächenfragen bei Kurven in Parameterdarstellung
1.8.6 Flächenfragen bei Kurven in Parameterdarstellung
|
Abschnitt 1.8.6
Seite 84
Auflage 1:
Seite 80
|
Bild von Ellipsenbeispiel fehlt noch XXXX |
Flächenbilanz zwischen Graph und x-Achse bei Parameterkurven
Flächenelement \(d A = y(t)\,\dot{x}(t)\,d t\)
Flächenbilanz \(A = \int_{t_a}^{t_{b}} y(t)\,\dot{x}(t) d t\)
|
 1.8.7 Flächenfragen bei Polardarstellung
1.8.7 Flächenfragen bei Polardarstellung
|
Abschnitt
1.8.7
Seite 85
Auflage 1:
Seite 81

|
|
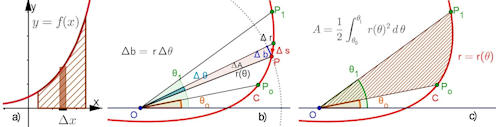
Abb. 1.54 Flächen und Kurven.
a) Fläche kartesisch, b) Ansatz für
Polarkurven: keilförmiges Flächenstück \(\Delta A\), das bei einer
Winkeländerung \(\Delta \theta\) entsteht. c) Die Fläche bei
Polarkurven ist ein Kurvensektor.

|
Abschnitt
1.8.7
Seite 86
Auflage 1:
Seite 82

|
|
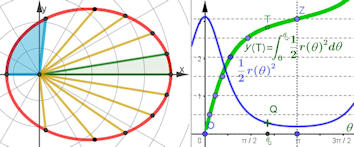
Abb. 1.55 1. und 2. Kepler'sches Gesetz.
Das Integral für die Sektoren der Polarkurve
\[
r(\theta)=\frac{p}{1-\varepsilon\cos\theta}
\]
erweist sich als sperrig. Der interaktive Weg zur Integration
wird im Text, aber auch im nächsten Zusatz erklärt.
 planeten-ellipsen-kepler.ggb
planeten-ellipsen-kepler.ggb 
|
 Zusatz Zusatz |
Sie sehen in diesem Bild die sogenannte "polar-kartesische Darstellung". Sie ist in diesem Webverbund häufig genutzt, insbesondere hier in www.kurven erkunden und verstehen erklärt.
Die Polargleichung \(r=r(\theta)\) wird als \(r=r(x)\) im 2. Grafikfenster kartesisch dargestellt. Ein Punkt \(K=(x,r(x))\) rechts kann dann als \(K=(r(\theta);\theta)\) im linken Grafikfenster ohne weitere Umrechnungen erscheinen. (In der *.ggb anwählbar.) Hier also wird das Integral \( y(T):=\int_0^t{\frac{1}{2}r(x)\ dx}\) kartesisch auf numerischem Weg berechnet und als Punkt \(T=(t,y(T))\) angezeigt. Da der bewegliche Punkt \(Q\) auf dem Integranden (blaue Kurve) \(t\) erzeugt, existiert die grüne Ortskurve von \(T \). Punkt \(Z\) an der Stelle \(\pi\)
gibt also die halbe Ellipsenfläche an. Rechts ist die Ordinate von
\(Z\) in 6 gleiche Teile, die Monate, geteilt. Die waagerechten Geraden schneiden die Ortslinie in Punkten, die als schwarze Punkte auf der Ellipse die Stellung der Erde im Monatsrhythmus zeigen. Die gelben Strecken heißen Fahrstrahlen. So ist das 2. Kepler'sche Gesetz visualisiert: In gleichen Zeiten überstreicht der Fahrstrahl gleiche Flächen.
 Im Kurvenbuch finden Sie zu den Keplerschen Gesetzen und speziell zu dem Flächenproblem auch eine Datei mit wahrer Flächenberechnung in GeoGebra-CAS Im Kurvenbuch finden Sie zu den Keplerschen Gesetzen und speziell zu dem Flächenproblem auch eine Datei mit wahrer Flächenberechnung in GeoGebra-CAS 
|
 1.8.8 Bogenlänge bei Funktionen und Parameterdarstellung
1.8.8 Bogenlänge bei Funktionen und Parameterdarstellung
|
Abschnitt
1.8.8
Seite 86
Auflage 1:
Seite 83

|
|
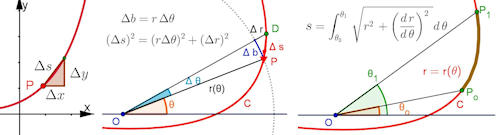
Abb. 1.56 Bogenlänge, links für kartesische Funktionen,
dann für Polarkurven, Ansatz und Ausführung.

|
 1.8.9 Bogenlänge von Polarkurven
1.8.9 Bogenlänge von Polarkurven
|
Abschnitt
1.8.8
1.8.9
Seite 87
Auflage 1:
Seite 84

|
|
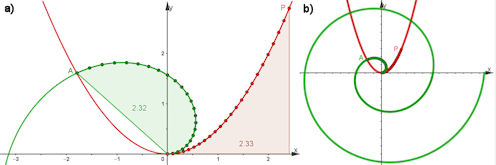
Abb. 1.57 Archimedische Spirale und
Parabel. a) zeigt Punkte auf der Spirale und der Parabel
\(y=\frac{1}{2}x^2\), die eine gleichlange Kette bilden und auch zu gleichen
Flächen führen, siehe Text.
In b) ist die Spirale bis \(\theta=4\pi\) dargestellt. Man kann sich
vorstellen, dass die Parabel bis zum Punkt \((12.6,\,79),\) den man hier gar
nicht mehr darstellen konnte, auf die grüne Spirale aufgewickelt worden ist.
 archimedes-bogen+flaeche.ggb
archimedes-bogen+flaeche.ggb
In dieser Datei ist zusätzlich dargestellt:
Der Bogen der Parabel von 0 bis \(2\pi\) und der entsprechende Bogen der archmedischen Spirale sind gleich lang.
Das Entsprechende gilt auch für Flächen von Pàrabel und Spirale.
|
 1.8.10 Volumen von Rotationskörpern
1.8.10 Volumen von Rotationskörpern
|
Abschnitt
1.8.10
Seite 89
Auflage 1:
Seite 85

|
|
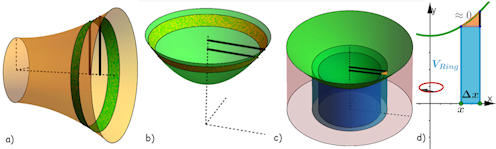
Abb. 1.58 Volumina bei Rotation einer Parabel.
a) Summation von senkrechten Zylinderscheibchen,
b) Summation von waagerechten Zylinderscheibchen,
c) Summation von aufrechten Zylinderringen,
d) halber Querschnitt des Zylinderringes.

|
 1.8.11 Uneigentliche Integrale
1.8.11 Uneigentliche Integrale
|
Abschnitt
1.8.11.1
Seite 90
Auflage 1:
Seite 86

|

 In der ggb-Datei sind auch das Bild und die Berechnung des Volumenintegrals mit GeoGebra-CAS. In der ggb-Datei sind auch das Bild und die Berechnung des Volumenintegrals mit GeoGebra-CAS.
|
Abb. 1.59 Uneigentliches Integral.
a) Zur grünen Funktion \(f(x)=\frac{1}{x}\) ist in Rot die bei \(x=1\)
beginnende Integralfunktion dargestellt. Die Ordinate bei \(B\) hat also den
Wert der braun hinterlegten Fläche, den Wert des Integrals.
Im Text wird über das Wachsen des Flächeninhalts nachgedacht, wenn \(B\) gegen
Unendlich rückt, dieser wird durch ein uneigentliches Integral
berechnet.
b) Wenn die in a) gezeigte Fläche um die x-Achse rotiert, entsteht
der blaue Trichter, den man sich bis ins Unendliche fortgesetzt denken soll.
Es wird sich zeigen, dass sein Volumen endlich ist, obwohl seine
Längsschnittfläche, in a) durch Braun und Hellblau angedeutet,
unendlichen Flächeninhalt hat.
 uneigen-trichter.ggb
uneigen-trichter.ggb 
|
Abschnitt
1.8.11.2
Seite 92
Auflage 1:
Seite 88

|
|
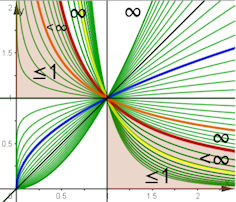
Abb. 1.56 Uneigentliche Integrale der Potenzfunktionen.
Die rote Kehrwertfunktion teilt
den 1. Quadranten auf in das obere Gebiet, in dem kein
uneigentliches Integral über \(x^k\) (grüne Graphen) konvergiert, und das
hellbraune, in dem alle konvergieren.
Farbig hervorgehoben sind (von rechts oben nach unten) schwarz: \(y=x\),
blau: \(y=x^{\frac{1}{2}}=\sqrt{x}\), schwarz: \(y=x^0=1\), orange:
\(y=x^{-\frac{1}{2}}=
\frac{1}{\sqrt{x}}\), rot: \(y=\frac{1}{x}\), gelb: \(y=\frac{1}{x^2}\).
Konvergenz:
\(\qquad I_k=-\frac{1}{k+1}\) für \(k<-1\)
\(\qquad I_a=\frac{1}{a+1}\) für
\(-1< a\leq0 \)
 uneigentlich-potenzen.ggb
uneigentlich-potenzen.ggb 
|
 1.9 Anwendungen der Integralrechnung
Weiter mit Kapitel 2 Lineare Algebra
1.9 Anwendungen der Integralrechnung
Weiter mit Kapitel 2 Lineare Algebra
|
|
|
|
|
 1.9.1 Harmonie der rotierten Quadriken
1.9.1 Harmonie der rotierten Quadriken
|
Abschnitt
1.9.1
Seite 92
Auflage 1:
Seite 88
 |
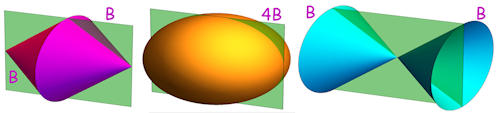
|
Abb. 1.61 Kegel und Ellipsoid. B ist der Volumen-Baustein \(\frac{1}{3}\pi\,a\,b^2\),
die grüne Fläche hat die Maße \(2a\times 2b\)

|
Abschnitt
1.9.1
Seite 92
Auflage 1:
Seite 89
|
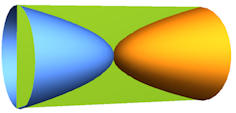
|
Abb. 1.62 Harmonie, rotierte Parabeln.
Parabeln mit dem Scheitel in O, die auf die
gezeigte Weise in den gedachten Kasten mit
den Seitenlängen (2a,2b,2b) passen, sind bisher
noch nicht dabei, sie „spielen aber auch mit“.
Diese liegenden Parabeln haben die Gleichung \(y^2=\frac{b^2}{a} x. \)
Ergibt sich auch ein Volumen mit B?
 Rotationsparabeln, Mathematica Quelltext
Rotationsparabeln, Mathematica Quelltext
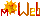 Dies zum Lesen und Verstehen
Dies zum Lesen und Verstehen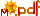
|
Abschnitt
1.9.1
Seite 94
Auflage 1:
Abschnitt
1.9.1.1
Seite 90
|

|
Abb. 1.63 Asymptoten-Kegel und Hyperboloid (bis 2a). B ist der Volumen-Baustein \(\frac{1}{3}\pi\,a\,b^2\).
Das Ellipsoid nimmt zwei Drittel des umfassenden Zylinders ein.
Es hat dasselbe Volumen wie das Hyperboloid.
Dieses halbiert genau seinen Asymptotenkegel.
Ein Ring der Breite d, irgendwo (ab a) aus dem Zwischenraum zwischen Hyperboloid und
Asymptoten-Kegel genommen, hat stets dasselbe Volumen wie eine Scheibe der Dicke d aus
dem gezeigten Zylinder.

|
Abschnitt
1.9.2
Seite 94
Auflage 1:
Abschnitt
1.9.1.1
Seite 90
|
|
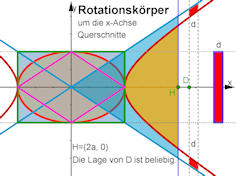
Abb. 1.64 Querschnitte zu den 3D-Abbildungen in diesem Abschnitt. Die verwendeten
Gleichungen sind z.B. \(\frac{x^2}{a^2}\pm\frac{y^2}{b^2}=1\) und \(y=\pm\frac{b}{a}x\).
Für die 3D-Bilder kommt zum \(y^2\)-Term stets ein ebensolcher \(z^2\)-Term hinzu.
Für den Zylinder z.B. anstelle von \(y^2=b^2\) nun \(y^2+z^2=b^2\).
Achten Sie darauf, dass Sie in Abschnitt~1.9.1.1
für "`Volumen zwischen"' nicht über die Differenz der Ordinaten integrieren
dürfen. Parabeln aus Abb. 1.58 sind hier nicht
eingetragen.
Lassen sie sich anregen, eigene Ideen zu verfolgen.
 harmonie.ggb
harmonie.ggb 
|
 1.9.2 Taylorreihen und Landau-Symbolik
1.9.2 Taylorreihen und Landau-Symbolik
|
Abschnitt
1.9.2.1
Seite 98
Auflage 1:
Seite 94
|
|
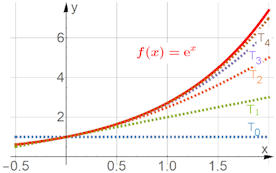
Abb. 1.65 Taylorpolynome
zu \({\rm e}^x\), entwickelt um \(x=0\). Die Taylorpolynome \(T_0(x)\) bis \(T_4(x)\) im
Vergleich mit der Exponentialfunktion selbst (gestrichelt). Die
Variable heißt hier wie üblich \(x\).
 TaylorExp.ggb
TaylorExp.ggb
|
Abschnitt
1.9.2.1
Seite 98
Auflage 1:
Seite 95
|
|
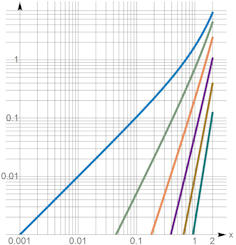
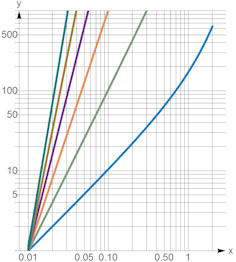
Abb. 1.66 Approximationsgüte zu
\({\rm e}^x\), entwickelt um \(x=0\). Die Differenz zwischen \({\rm e}^x\) und den
Taylorpolynomen \(T_0(x)\) bis \(T_5(x)\) ist hier doppelt-logarithmisch
dargestellt. Näheres zum rechten Bildteil steht im Text, die x-Achse schneidet
hier die y-Achse bei \(y=1\).
 TaylorApproximationsGüte, Mathematica Quelltext
TaylorApproximationsGüte, Mathematica Quelltext
 Dies zum Lesen und Verstehen
Dies zum Lesen und Verstehen
|
 Zusatz zu Zusatz zu
Abschnitt 1.9.2.1
Seite 96-99
Auflage 1:
Seite 93-96
|
Restglieder für Taylorreihen: Nutzen und Problematik
Möglicherweise hat die Leserin in unserem Buch im Zusammenhang mit der
Taylorapproximation die Erwähnung des Restgliedes
\(R_{n+1}\) vermisst. Es besagt, dass die folgende Gleichung gilt:
\[
f(x) = T_n(x) + R_{n+1}(x)\quad\text{mit}\quad R_{n+1}(x) =
\frac{1}{(n+1)!}f^{(n+1)}(\xi)(x-x_0)^{n+1}.
\]
Das Restglied sieht aus wie der neue Summand im nächsten
Taylorpolynom, allerdings wird die \((n+1)\)-te Ableitung von \(f\) nicht
an der Stelle \(x_0\) ausgewertet, sondern an der Stelle \(\xi\).
Dabei ist \(\xi\) eine bestimmte Zahl im Intervall \([x_0,x]\), die aber
i.A. nicht leicht zu finden ist. Wenn \(f^{(n+1)}\) im genannten
Intervall monoton ist, kann man aber
\[
T_n(x) + R_{n+1}(x)|_{\xi=x_0} \le f(x) \le
T_n(x) + R_{n+1}(x)|_{\xi=x}
\]
nutzen, um den Funktionswert \(f(x)\) genauer einzugrenzen. Eventuell
müssen die Zeichen \(\le\) durch \(\ge\) ersetzt werden, dass hängt davon
ab, wie \(f^{(n+1)}\) genau verläuft.
Diese Eingrenzung erfordert aber eine weitere Ableitung von \(f\), ist
umständlich zu nutzen und schon in manchen einfachen Fällen absolut
nutzlos, wie das folgende Beispiel zeigt:
Wir wählen \(f(x) = \frac{1}{1-x}\), entwickeln um \(x_0 = 0\), und
erhalten
\[
T_n(x) = 1 + x + x^2 + x^3 + \dots + x^n,\quad
R_{n+1}(x) = \frac{1}{(1-\xi)^{n+1}}x^{n+1}.
\]
Versuchen wir einmal \(x=0.6=\frac{3}{5}\). Es ist
\[
f(0.6) = 2.5,\quad T_n(0.6) = 2.5\cdot(1-0.6^{n+1}),\quad
R_{n+1}(x)|_{\xi=0} = 0.6^{n+1},\quad
R_{n+1}(x)|_{\xi=0.6} = 2.5\cdot1.5^{n+1}.
\]
Das letzte Restglied geht aber gegen \(\infty\), wenn der Grad
des Taylorpolynoms immer weiter erhöht wird! Z.B. wird für \(n=4\)
\[
T_4(0.6) = 2.3056,\quad R_5(x)|_{\xi=0} = 0.0778,\quad
R_5(x)|_{\xi=0.6} = 18.9844,
\]
das ergibt die Eingrenzung
\[
2.3056 + 0.0778 = 2.3834 \le f(0.6) \le 2.3056 + 18.9844 = 21.2900,
\]
das ist zwar korrekt, aber wenig hilfreich.
|
Abschnitt
1.9.2.3
Seite 100
Auflage 1:
Abschnitt
1.9.2.2
Seite 96
|
|
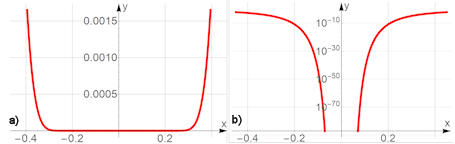
Abb. 1.67 \(f(x)={\rm e}^{^{-\frac{1}{x^2}}}\)
ist nicht analytisch. a) zeigt den Graphen der Funktion in normaler
Darstellung, in b) sind die Funktionswerte logarithmisch abgetragen.
Erst hier wird deutlich, wie schnell und stark die Werte gegen null gehen.
 TaylorExp-x(-2), Mathematica Quelltext
TaylorExp-x(-2), Mathematica Quelltext
 Dies zum Lesen und Verstehen Dies zum Lesen und Verstehen
|
Abschnitt
1.9.2.3
Seite 100
Auflage 1:
Seite 97
|
|
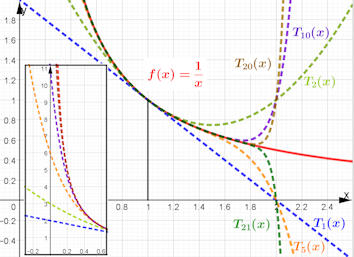
Abb. 1.68 Taylorpolynome zu \(1/x\), entwickelt um \(x=1\).
Die Taylorpolynome \(T_n(x)\) für
\(n=1,2,5,10,20,21\)
(gestrichelt) im Vergleich mit der Funktion selbst.
Nahe \(x=2\) streben die
Taylorpolynome für gerades \(n\) zum
Näherungswert 1, für ungerades \(n\) zum Näherungswert 0, obwohl
\(f(2)=\frac{1}{2}\) ist. Alle
Approximationen sind dort sehr schlecht.
Das links eingefügte kleine Bild zeigt, dass es nahe \(x=0\) nicht
besser ist - aber das kann man in der Nähe einer Polstelle auch nicht
erwarten.
 Taylorfuer1durchx.ggb
Taylorfuer1durchx.ggb
|
 1.9.3 Kriterien für Extrema und Wendepunkte
1.9.3 Kriterien für Extrema und Wendepunkte
|
Abschnitt
1.9.3
Seite 101
Auflage 1:
Seite 97
|
|
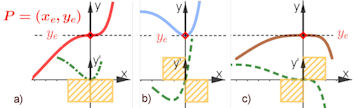
Abb. 1.69 Graphen
von \(f\) und \(f'\) nahe einer möglichen Extremstelle in \(x_e\). Wechselt \(f'\)
bei \(x_e\) das Vorzeichen nicht, dann ist \(f\) mononton.
Wechselt \(f'\) das Vorzeichen bei \(x_e\), dann ist \(x_e\) Extremstelle.

|
Abschnitt
1.9.3
Seite 103
Auflage 1:
Seite 100
|
|
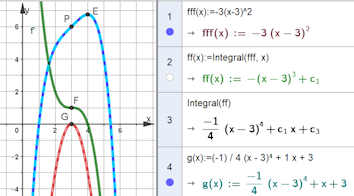
Abb. 1.70 Polynom mit Plattstelle. Es ist
\(f(x)=\frac{1}{4}\bigl(-x^4+12x^3-54x^2+112-69\bigr)\) (blauer Graph).
Die Ableitungen sind: \\
\(f'(x)=\frac{1}{4}\bigl(-4x^3+36x^2-108x+112\bigr)\) (grüner Graph) und \\
\(f''(x)=\frac{1}{4}\bigl(-12x^2+72x-108\bigr)=-3\bigl(x^2-6x+9\bigr)=-3(x-3)^2\)
(roter Graph).
Die Berührung der x-Achse durch \(f''\) in \(G\) garantiert die Krümmung null in
\(f\) und Steigung null in \(f'\). Da \(f''\) in \(G\) aber nicht das
Vorzeichen wechselt, liegt bei \(f'\) kein Extremum, sondern ein Sattelpunkt in
\(F=(3,1)\) vor. Da \(f'\) in \(x=3\) ebenfalls nicht das Vorzeichen
wechselt, hat \(f\) in \(P=(3,6)\) als einzige Besonderheit die Krümmung null.
Dies passt zu Satz 1.19, erst die vierte Ableitung von \(f\) ist
wieder von null verschieden.
 plattstelle.ggb
plattstelle.ggb 
|
 Zusatz Zusatz |
Zu Abb. 1.70 b): Eine Aufgabe mit einer Plattstelle baut man von unten auf, wie hier mit GeoGebra-CAS gezeigt. Man fängt mit einer Parabel an, die ihren Scheitel auf der x-Achse hat, und integriert sie zweimal. die Integrationskonstanten kann man frei wählen, eine Plattstelle fordert \(c_1\neq 0\). Die entstehenden Funktionen werden von dem CAS gleich im Grafikfenster eingetragen. Daher muss man andere Bezeichnungen wählen.
|
Abschnitt
1.9.3
Seite 104
Auflage 1:
Seite 101
|
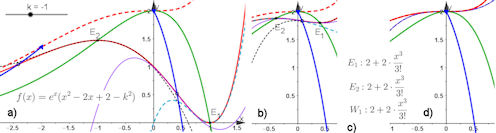
 An \(x_E=\pm k\) und \( x_W=\pm \sqrt{1+k^2}-1 \) sehen wir, dass die Extrema genau für \(k=0\) zusammenfallen, dass aber die Wendepunkte für \(k=0\)
verschieden sind. Der eine fällt mit dem Extremum zusammen. In der Datei sind mit dem CAS diese Terme berechnet worden. An \(x_E=\pm k\) und \( x_W=\pm \sqrt{1+k^2}-1 \) sehen wir, dass die Extrema genau für \(k=0\) zusammenfallen, dass aber die Wendepunkte für \(k=0\)
verschieden sind. Der eine fällt mit dem Extremum zusammen. In der Datei sind mit dem CAS diese Terme berechnet worden.
|
Abb. 1.71 Extrema werden zum
Sattelpunkt. In a) ist eine Funktion (rot) aus einer Funktionenschar
gezeigt, deren zwei Extrema mit wachsendem \(k\) auf der grünen Kurve nach oben
wandern und dabei zusammenrücken, ihre beiden Wendepunkte wandern auf den
blauen Kurven nach oben. Zusätzlich sind dargestellt die
Taylorpolynome dritten Grades, entwickelt für \(E_1,\,E_2\) (dünn gestrichelt)
und den Wendepunkt dazwischen (dünn blau). In b) ist für \(k=-0.4\) der
Graph von \(f\) schon dicht an der rot gestrichelten Grenzlage der Schar, in der
die Extrema zusammenfallen. Die Formeln der Taylorpolynome in c)
zeigen, dass sie für \(k=0\) zusammengefallen sind in eine
Sattelfunktion. In d) ist für \(k=0\) auch \(f\) als Funktion mit
Sattel ohne Extrema zu sehen.
Wenn \(k\) weiter wächst, tauschen \(E_1\) und \(E_2\) ihre Plätze und
wandern ebenso wie die Wendepunkte auf ihren Kurven wieder nach unten.
 e-k-ex-sattel.ggb
e-k-ex-sattel.ggb 
|
 1.9.4 Regel von L'Hospital
1.9.4 Regel von L'Hospital
|
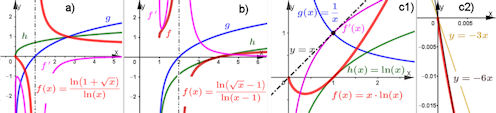
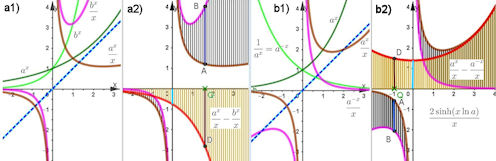
 zu Abb. 1.74 a),
zu Abb. 1.74 a),  zu Abb. 1.74 b)
zu Abb. 1.74 b)
 zu Abb. 1.75,
zu Abb. 1.75,  zu Abb. 1.77
zu Abb. 1.77