ISBN 978 662 69291 2 Auflage 2 Book Springer Spektrum
ISBN 978 662 69292 9 Auflage 2 eBook
www.mathematik-sehen-und-verstehen.de
https://masuv.web.leuphana.de (Sicherer Zugang)
Dieter Riebesehl
Hubert Dammer |
Höhere Mathematik sehen und verstehen
ISBN 978 662 69291 2 Auflage 2 Book Springer Spektrum ISBN 978 662 69292 9 Auflage 2 eBook www.mathematik-sehen-und-verstehen.de https://masuv.web.leuphana.de (Sicherer Zugang) |
Dörte Haftendorn Dieter Riebesehl Hubert Dammer |
|
Anregungen mit Lösungen zu Kapitel 1  |
| Anregung 1.1 | Vertrautheit mit der Gaußschen Zahlenebene | Anregung 1.5 | Flächen bei PotenzFunktionen |
| Anregung 1.2 | Logarithmus und Gleichungen | Anregung 1.6 | Eulerkasten |
| Anregung 1.3 | Polynome \(p3\) im Affenkasten | Anregung 1.7 | Zur Regel von L'Hospital |
| Anregung 1.4 | Polynome \(p4\) im Pantherkäfig | Anregung 1.8 | Komplexe Fourier-Koeffizienten |
| Anregung 1.1
Abschnitt 1.2.2 Seite 9 |
Vertrautheit mit der Gauß'schen Zahlenebene 1. Betrachten Sie eine komplexe Zahl \(z\) im 2. Quadranten  .
Machen Sie sich durch kleine Skizzen
klar, in welchen Quadranten dann \(z^2,\; z^3,\;3{\rm i}\cdot 2z,\;3{\rm i} +2z,\; \bar{z},\; \frac{1}{z}\;
\text{ und } \frac{1}{\bar{z}}\) liegen. 2. Betrachten Sie \(z=12+{\rm i}\,n\) mit \(n\in \mathbb Z\). Für welche \(n\) liegen diese komplexen Zahlen innerhalb des Kreises um 0 mit Radius \(r=30\)? 3. Welche komplexen Zahlen \(z\) haben die Eigenschaft \(|z|=|\Re(z)|+|\Im(z)|\)? 4. Zeichnen Sie \(z=4+3\,{\rm i}\) und berechnen den Betrag. Überrascht Sie das Ergebnis? Informieren Sie sich Über "pythagoräische Zahlentripel". Was haben sie mit dieser Aufgabe zu tun? 5. Definieren Sie in GeoGebra \(b=0.5+0.7{\rm i}\). Setzen Sie \(\{b,\,b^2,\,b^3,\,b^4,\,b^5,\,b^6\}\) in die Zeichenebene und verbinden Sie sie mit einem Polygonzug. Ziehen Sie dann an \(b\). Was beobachten Sie? 6. Zeichnen Sie in GeoGebra ein reguläres \(n\)-Eck im Einheitskreis mit Hilfe von \(a={\rm e}^{{\rm i}\,\varphi}\), siehe Abschnitt 1.2.1.1. |
Lösungen zu 1.1
1. Für das Argument \(\varphi\) von \(z\) gilt \(\frac{\pi}{2}\le\varphi\le\pi\). Für die Argumente von \(z^2,\; z^3,\;3{\rm i}\cdot 2z,\;3{\rm i} +2z,\; \text{ und } \frac{1}{z}\) hat man dann (in dieser Reihenfolge) die Bereiche \(\pi\le\varphi\le2\pi\), \(\frac{3\pi}{2}\le\varphi\le3\pi\), \(\pi\le\varphi\le\frac{3\pi}{2}\), \(\frac{\pi}{2}\le\varphi\le\pi\), \(\frac{3\pi}{2}\le\varphi\le2\pi\). Das sind in Quadranten: 3.-4.; 1., 2. oder 4.; 3.; 2.; 3. Quadrant. Für \(\bar{z} \text{ und } \frac{1}{\bar{z}}\) wird der Quadrant von \(z\) bzw. \(\frac{1}{z}\) an der reellen Achse gespiegelt, man erhält also den 3. bzw. 1. Quadranten. 2. Es soll sein \(|z| = \sqrt{144+n^2}\le30\), also \(144+n^2\le900,\ n^2\le756,\ n\le27\). 3. Mit \(z=a+{\rm i}b\) muss \(a^2+b^2 = (|a|+|b|)^2\) gelten, also \(0 = 2|a||b|\), das geht nur, wenn \(a=0\) oder \(b=0\) ist. Die komplexen Zahlen mit dieser Eigenschaft liegen also auf der reellen oder der imaginären Achse. 4. Man erhält sofort \(|z|=5\), also wieder eine ganze Zahl. Anders geschrieben ist \(3^2+4^2 = 5^2\). Solche Tripel von ganzen Zahlen heißen "pythagoräisch". Sie sind ganzzahlige Seiten von rechtwinkligen Dreiecken. 5. Dies mässen Sie tun! Die folgende Beschreibung gibt den Effekt nur unzureichend wieder: Der Polygonzug hat die Form einer approximierten logarithmischen Spirale, die beim Ziehen an \(b\) gestreckt und gestaucht wird. Ist \(b\) reell, entartet die Spirale zu einer Strecke. Eine Geogebra-Datei zum Ausprobieren finden Sie unter folgendem Link: 
b-Potenzen.ggb Und so sehen Beispiele aus: 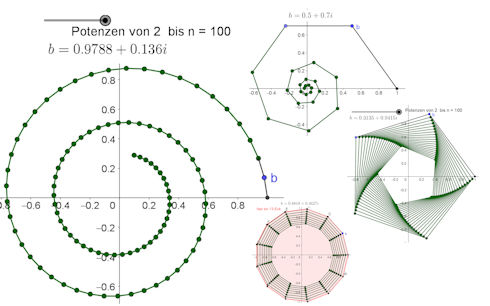 Wann wickelt sich die Spirale ein, wann wird sie größer?
6. Dazu muss \(a\) als komplexe Zahl eine Ecke des \(n\)-Ecks sein. Die Potenzen \(a^2,\ a^3,\ \dots,\ a^n\) ergeben dann die anderen Ecken. Damit sich das \(n\)-Eck schließt, muss \(a^n = 1\) sein, das erfordert \(n\varphi = 2\pi\), also \(\varphi = \frac{2\pi}{n}\). |
|||
|
Anregung 1.2
Abschnitt 1.5.3.3 Seite 33 |
1.2 Gleichung mit Logarithmus lösen \( \begin{array}{l} \text{1)$\quad$ Finden Sie $x$: $\quad$} a^{5 x+1}=32a \qquad~ & \qquad\\ \text{2)$\quad$ Vereinfachen Sie: $\quad$} \big({\rm e}^{b\ln(c)}\big)^{-\frac{2}{b}} \qquad~ & \qquad\\ \text{3)$\quad$ Finden Sie $x$: $\quad$} 3^{2x+1}=5^x\\ \text{4)$\quad$ Finden Sie $x$: $\quad$} 2\cdot4^x + 10^x = 25^x\\ \end{array} \) Dividieren Sie in 4) die Gleichung durch \(4^x\). Daraus resultiert eine quadratische Gleichung fuuml;r eine geschickt gewählte Potenz! |
Lösung zu 1.2 \( \begin{array}{l} \text{1)$\quad$} a^{5 x+1}=32a \Rightarrow (a^{x})^5 = 32 \Rightarrow a^x = 2 \Rightarrow x = \frac{\ln2}{\ln a}\\ \text{2)$\quad$} \big({\rm e}^{b\ln(c)}\big)^{-\frac{2}{b}} = {\rm e}^{-2\ln c} = c^{-2} = \frac{1}{c^2} \\ \text{3)$\quad$} 3^{2x+1}=5^x \Rightarrow 3\cdot9^x = 5^x \Rightarrow 3 = \left(\frac{5}{9}\right)^x \Rightarrow x = \frac{\ln3}{\ln5 - \ln9}\\ \text{4)$\quad$} 2\cdot4^x + 10^x = 25^x \Rightarrow 2 + \left(\frac{10}{4}\right)^x = \left(\frac{25}{4}\right)^x \Rightarrow 2 + \left(\frac{5}{2}\right)^x = \left(\frac{5}{2}\right)^{2x},\\ \text{dies ist eine quadratische Gleichung für}\ \left(\frac{5}{2}\right)^x\ \text{mit den Lösungen}\ \left(\frac{5}{2}\right)^x = -1\ \text{und}\ \left(\frac{5}{2}\right)^x = 2.\\ \text{Die negative Lösung kann keine Potenz von}\ \left(\frac{5}{2}\right)\ \text{sein, deshalb verbleibt}\\ x = \frac{\ln2}{\ln5 - \ln2}. \end{array} \) |
||||
|
Anregung 1.3
Abschnitt 1.8.3.4 Seite 78 |
1.3 (Erkundung der Polynome 3. Grades)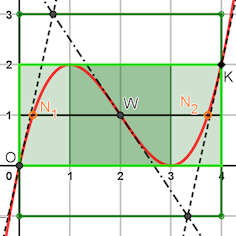
Abb. 1.50 Polynome im Affenkasten Betrachten Sie das Polynom: \(p(x)=\frac{1}{2}x(x-3)^2\) Die Extrema von \(p\) definieren in der gezeigten Art einen dunkelgrünen Kasten mit vier Zellen, der in Hellgrün auf 8 Zellen erweitert ist. Im Zentrum ist der Wendepunkt \(W\). Weisen Sie nach, dass die Kastenecke \(K\) ein Kurvenpunkt ist. Die Betrachtung der Flächen -- z.B. zwischen \(y{=}1\) von \(N_1\) bis \(W\) oder zwischen x-Achse und Kurve von \(O\) bis Minimumstelle, u.a. -- bietet einige Besonderheiten, viele Flächenverhältnisse sind rational. Hinweis Jedes Polynom 3. Grades hat genau einen Wendepunkt \(W\). Ein beliebiger Kurvenpunkt \(P\) definiert mit seiner Tangente, der zu ihr parallelen Geraden durch \(W\) und den Senkrechten durch \(P\)und \(W\) eine Parallelogramm-Zelle. Acht solche Zellen mit \(W\) im Zentrum bilden einen schrägen Affenkasten mit allen oben angesprochenen Eigenschaften. Der Name ist gewählt, weil jedes Polynom 3. Grades in jeden solchen Kasten gesperrt werden kann. Der Kasten im Bild ist nur ein Sonderfall. Mittelalterliche Gaukler präsentierten auf Märkten ihre Affen in Kästen. In Abb. 1.50 lohnt sich auch der Vergleich mit den Kastenzellen. Diese haben hier die Fläche \(Z=1\), im Allgemeinen: \(Z=(x_W-x_{max})(y_{max}-y_W)\). Wendetangente und Randtangenten schneiden sich auf den Kanten eines doppelt so hohen Kastens, mit ihnen ergeben sich weitere besondere Flächen. Jedes Polynom 3. Grades mit Extrema hat so einen Kasten mit diesen Eigenschaften. |
Lösung zu 1.3
|
||||||||
| Anregung 1.4
Abschnitt 1.8.3.4 Seite 79 |
1.4 (Erkundung der Polynome 4. Grades)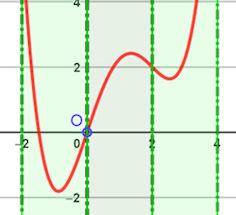
Abb. 1.51 Polynome 4. Grades im Pantherkäfig Es geht beispielhaft um \(p(x)=\frac{1}{4} x^4 -x^3 + 3x\). Die Wendepunkte definieren einen „Pantherkäfig“ mit vier Stangen, d.h. senkrechten Geraden, in gleichem Abstand. Lesen Sie das Gedicht von Rainer Maria Rilke: "`Der Panther". Aufgaben
Beachten Sie, dass der Grund für diese Zusammenhänge darin liegt, dass Polynome 4. Grades mit mehreren Extrema immer als zweite Ableitung eine Parabel mit zwei verschieden Nullstellen haben müssen. |
Lösung zu 1.4
|
||||||||
| Anregung 1.5
Abschnitt 1.8.3.4 Seite 80 |
1.5 (Besondere Flächen bei Potenzfunktionen)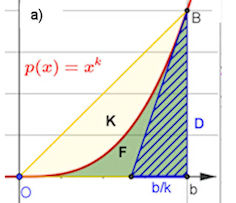
Abb. 1.5.2 Eine Potenzfunktion mit Exponent \(k\) Zu a): Das Segment K ist begrenzt von der Potenzfunktion mit Exponent \(k,\; k>1\), und der Strecke \(\overline{OB}\), die Fläche F wird gebildet von der Potenzfunktion, ihrer Tangente in \(B\) und der x-Achse. Zeigen Sie, dass gilt: \(\frac{K}{F}=\frac{k}{1} \leftrightarrow K=k\cdot F\)
|
Lösung zu 1.5
|
||||||||
| Anregung 1.6
Abschnitt 1.8.3.4 Seite 80 |
1.6 (Eulerkasten, Flächen bei verketteter e-Funktion)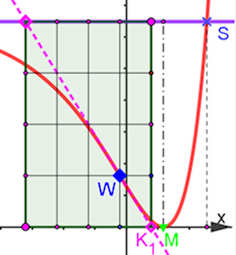
Abb. 1.53 Der Eulerkasten von \(f(x)=({\rm e}^x-k)^2\) Bei dieser Funktion lohnt es sich besonders, die Gestalt des Graphen durch Abwärtsschieben der e-Funktion und Quadrieren zu verstehen. Die Flächen, die im Folgenden betrachtet werden und die Sie mit Integralen berechnen können, befinden sich alle zwischen der Asymptote und dem Graphen von \(f\), der roten Kurve. Sei \(Z\) die Fläche einer der 16 gleichen Kastenzellen. Erstaunlicherweise lassen sich viele der Flächen als ganzzahlige Vielfache von \(Z\) oder \(\frac{1}{2}Z\) ausdrücken. Aufgaben konkret
|
Lösung zu 1.6
|
| Anregung 1.7
Abschnitt 1.9.4 Seite 11 |
1.7 Zur Regel von L'Hospital Die Regel von L'Hospital führt nicht immer zum Ziel. Der Leser versuche einmal, sie auf folgende Grenzwerte anzuwenden: \begin{align*} \lim_{x\to\infty}\,&\,\frac{{\rm e}^x-{\rm e}^{-x}}{{\rm e}^x+{\rm e}^{-x}} &\\ \lim_{x\to 0}\,&\,\frac{x^2\cos\left(\frac{1}{x}\right)}{\sin x}, &\\ \lim_{x\to\infty}\,&\,\frac{3x}{\sqrt{2x^2-1}}. \end{align*} |
Lösung zu 1.7 Die Anwendung der Regel von l'Hospital in (*) führt der Reihe nach zu folgenden Zwischenergebnissen: \begin{align*} \lim_{x\to\infty}\,\frac{{\rm e}^x-{\rm e}^{-x}}{{\rm e}^x+{\rm e}^{-x}} &\stackrel{(*)}= \lim_{x\to\infty}\,\frac{{\rm e}^x+{\rm e}^{-x}}{{\rm e}^x-{\rm e}^{-x}} \stackrel{(*)}= \lim_{x\to\infty}\,\frac{{\rm e}^x-{\rm e}^{-x}}{{\rm e}^x+{\rm e}^{-x}} \stackrel{(*)}= \dots,\qquad \text{es gibt keinen Fortschritt mehr.}\\ \lim_{x\to 0}\,\frac{x^2\cos\left(\frac{1}{x}\right)}{\sin x} &\stackrel{(*)}= \lim_{x\to 0}\,\frac{2x\cos\left(\frac{1}{x}\right)+\sin\left(\frac{1}{x}\right)}{\cos x}, \qquad \text{der Zähler ist nicht mehr differenzierbar, l'Hospital nicht mehr anwendbar.} \\ \lim_{x\to\infty}\,\frac{3x}{\sqrt{2x^2-1}} &\stackrel{(*)}= \lim_{x\to\infty}\,\frac{3}{\frac{2x}{\sqrt{2x^2-1}}} = \lim_{x\to\infty}\,\frac{3\sqrt{2x^2-1}}{2x} \stackrel{(*)}= \lim_{x\to\infty}\,\frac{3\frac{2x}{\sqrt{2x^2-1}}}{2} = \lim_{x\to\infty}\,\frac{3x}{\sqrt{2x^2-1}} \dots \end{align*} In allen Fällen helfen einfache Umformungen weiter: \begin{align*} \lim_{x\to\infty}\,\frac{{\rm e}^x-{\rm e}^{-x}}{{\rm e}^x+{\rm e}^{-x}} &= \lim_{x\to\infty}\,\frac{1-{\rm e}^{-2x}}{1+{\rm e}^{-2x}} = 1.\\ \lim_{x\to 0}\,\frac{x^2\cos\left(\frac{1}{x}\right)}{\sin x} &= \lim_{x\to 0}\,\frac{x\cos\left(\frac{1}{x}\right)}{\frac{\sin x}{x}} = \frac{\lim_{x\to 0}\,x\cos\left(\frac{1}{x}\right)}{\lim_{x\to 0}\,\frac{\sin x}{x}} = \frac{0}{1} = 0.\\ \lim_{x\to\infty}\,\frac{3x}{\sqrt{2x^2-1}} &= \lim_{x\to\infty}\,\frac{3}{\frac{1}{x}\sqrt{2x^2-1}} = \lim_{x\to\infty}\,\frac{3}{\sqrt{2-\frac{1}{x^2}}} = \frac{3}{\sqrt2}. \end{align*} |
|||
| Anregung 1.8
Abschnitt 1.9.5.3 Seite 120 |
1.8 Komplexe Fourierkoeffizienten Prüfen Sie die Formel \begin{align*} c_n &= \frac{1}{2\pi}\int_0^{2\pi} f(x){\rm e}^{-{\rm i} nx} {\rm d} x. \end{align*} nach, indem Sie die Formeln für die reellen Fourierkoeffizienten zusammensetzen, um die \(c_n\) zu bekommen, und dann die Euler'sche Formel unter dem Integral anwenden. Was passiert für \(c_0\)? |
Lösung zu 1.8 \begin{align*} c_n &= \frac{a_n - b_n{\rm i}}{2} = \frac{1}{2\pi}\int_0^{2\pi} f(x)\cos nx {\rm d} x - \frac{{\rm i}}{2\pi}\int_0^{2\pi} f(x)\sin nx {\rm d} x = \\ &= \frac{1}{2\pi}\int_0^{2\pi} f(x)(\cos nx - {\rm i}\sin nx) {\rm d} x = \frac{1}{2\pi}\int_0^{2\pi} f(x)(\cos(-nx) + {\rm i}\sin(-nx)) {\rm d} x = \\ &= \frac{1}{2\pi}\int_0^{2\pi} f(x){\rm e}^{-{\rm i} nx} {\rm d} x. \end{align*} Für \(c_0\) ergibt sich direkt \begin{align*} c_0 &= \frac{1}{2\pi}\int_0^{2\pi} f(x) {\rm d} x = \frac{a_0}{2}. \end{align*} |
|||
|
|||||||
 Prof. Dr. Dörte Haftendorn
| Prof. Dr. Dieter Riebesehl
| Dipl.-Math. Dipl.-Ing. Hubert Dammer
|
|||||
Wir arbeiten noch an dieser Baustelle
