ISBN 978 662 69291 2 Auflage 2 Book Springer Spektrum
ISBN 978 662 69292 9 Auflage 2 eBook
www.mathematik-sehen-und-verstehen.de
https://masuv.web.leuphana.de (Sicherer Zugang)
Dieter Riebesehl
| Höhere Mathematik sehen und verstehen
ISBN 978 662 69291 2 Auflage 2 Book Springer Spektrum ISBN 978 662 69292 9 Auflage 2 eBook www.mathematik-sehen-und-verstehen.de https://masuv.web.leuphana.de (Sicherer Zugang) |
Dörte Haftendorn Dieter Riebesehl |
| 4 Differentialgleichungen, DGLn | |||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
| Abschnitt 4.1 Seite 308 Auflage 1: Seite 284 |
|
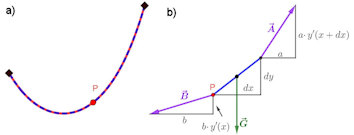
Abb. 4.1 Kettenlinie.
a) An zwei festen Punkten hängt eine Kette, eine gleichmäßig verteilte Linienlast. b) Skizze zur Herleitung der DGL der Kettenlinie aus den wirkenden Kräften. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Anregung 4.1
Abschnitt 4.3.2.1 Seite 315
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abschnitt 4.2 Seite 310f Auflage 1: Seite 285f |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abschnitt 4.3.2 Seite 312 Auflage 1: Seite 288 |
|
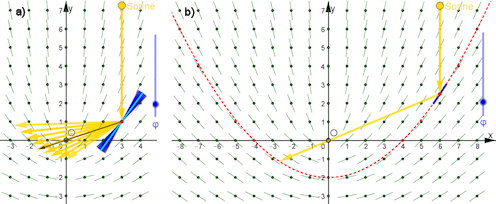
Abb. 4.2 Sammeln von Sonnenlicht. Die senkrecht von oben parallel einfallenden Sonnenstrahlen
sollen durch einen kleinen Spiegel (blau) auf den Ursprung gelenkt werden. a) zeigt,
wie der Neigungswinkel φ des Spiegels verändert wird, bis der gespiegelte Sonnenstrahl wirklich
durch den Ursprung geht. b) zeigt für viele Punkte richtige Spiegelstellungen und einen
typischen Lichtstrahl. Gesucht ist - und hier in Rot gefunden - eine Kurve, eine Funktion, die
zu dem so entstandenen Richtungsfeld passt.
|
||||||||||||
| Abschnitt 4.3.2 Seite 313 Auflage 1: Seite 289 |
|
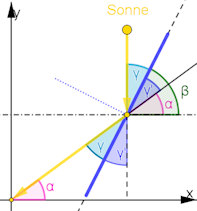
Abb. 4.3 Berechnung der Neigung eines Spiegels. Ein Spiegelstück aus Abb. 4.2 ist hier gezeigt: Die Reflexionswinkel γ und ihre Scheitelwinkel γ' sind gleich groß. β ist der Neigungswinkel des Spiegels, also der Steigungswinkel der gesuchten Funktion.
|
||||||||||||
| Abschnitt 4.3.2.2 Seite 316 Auflage 1: Seite 292 Lösungen, Lösungswege: Abschnitt 4.5.11 Seite 323 |
|
Abb. 4.4 Richtungsfelder für explizite DGLn 1. Ordnung. a) und d) sind lineare DGLn mit nicht konstanten Koeffizienten, b) ist eine solche mit konstanten Koeffizienten, c) ist eine DGL 2. Grades mit konstanten Koeffizienten. Alle vier Dateien sind
mm=Folge(Folge(1/5 (9 - t²), s, xmin, xmax), t, ymin, ymax) ist der rote Term durch Ihre Funktion f(s,t) zu ersetzen. Als Laufindizes stehen s für x und t für y. Den Befehl Richtungsfeld (dieser Dateien) müssen Sie unverändert übernehmen, die Bildgrenzen xmax... müssen natürlich vorher festgelegt sein. |
||||||||||||
| Abschnitt 4.3.3 Seite 317 Auflage 1: Seite 293 |
|
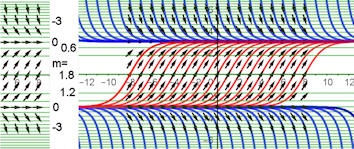
Abb. 4.5 Die Isoklinen der logistischen DGL. Für m ≤ 1.8 sind sie hier grün
mit einer Schrittweite von 0.6 für m eingezeichnet.
In dem Bereich zwischen den Geraden y = ±3 liegen, rot dargestellt, die „eigentlichen" logistischen Kurven. Auch die blauen Kurven sind Lösungen. Einige sind eingezeichnet, aber sie können durch Ziehen von A und B mehr davon sehen. |
||||||||||||
| Abschnitt 4.3.3 Seite 318 Auflage 1: Seite 294 |
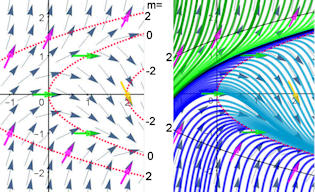
|
Abb. 4.6 Isoklinen-Parabeln für die DGL y' = y2 - x entstehen wegen m = y2 - x ⇔ y2 = x + m als nach rechts geöffnete und verschobene Normalparabeln, die m-Isokline hat
ihren Scheitel in (-m, 0). Die Null-Isokline enthält den Ursprung. In der Mitte der Pfeile ist die angezeigte
Pfeilrichtung gültig, was man an den Isoklinen-Parabeln sieht.
Rechts sind Lösungskurven eingezeichnet. Auf diese gehen wir bei Abb. 5.35 und 5.36 ein. Die Grenze zwischen den grünen und den blauen Lösungen wird in Abschnitt 5.65 exakt berechnet und in Abb. 5.45 (violett)dargestellt. |
||||||||||||
| Abschnitt 4.3.4 Seite 320 Auflage 1: Seite 296 |
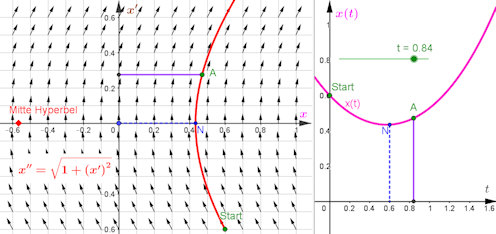
|
Abb. 4.7 Phasenraumdiagramm zur Kettenlinie. Links ist das Richtungsfeld zur DGL
\(x'' = \sqrt{1+(x')^2}\)
im Phasenraum zu sehen, man sagt auch Phasenraumdiagramm, dazu eine (rote)
Lösungskurve im Phasenraum mit Startpunkt und einem Kurvenpunkt A = (x, x'), rechts ist
violett die zugehörige Lösungskurve (t, x(t)) der Kettenlinien-DGL im tx-System gezeichnet. Auf
ihr liegen der Start, A = (t, x(t)) und N = (xe, 0), die Abszissen dieser Punkte im linken Bild
sind im rechten die Ordinaten, dort haben diese Punkte als Abszissen den Zeitpunkt t, zu dem
sie erreicht werden. Auf der Website ist A animiert. Nach einem Start, hier für t = 0, ergibt
sich für t das x(t) und damit A rechts, links gehört zu diesem A und seinem x(t) noch x'(t)
und die im Richtungsfeld angezeigte Richtung. N ist der Scheitel der Kettenlinie.
|
||||||||||||
| Abschnitt 4.3.4.1 Seite 322 Auflage 1: Seite 298 |
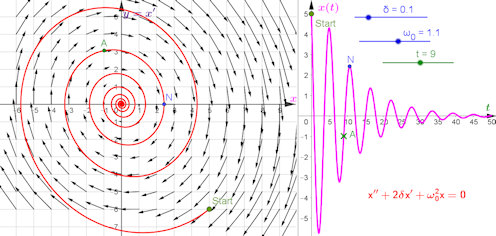
|
Abb. 4.8 Phasenraumdiagramm zur gedampften Schwingung. Der Aufbau ist ebenso wie
in Abb. 4.7 in Beispiel 4.1, zusatzlich kann man an Schiebereglern δ und ω0 einstellen.
|
||||||||||||
|
Anregung 4.2
Abschnitt 4.3.4.1 Seite 322
|
|
|||||||||||||
| Abschnitt 4.3.4.1 Seite 323 Auflage 1: Seite 299 Beispiel 4.6 |
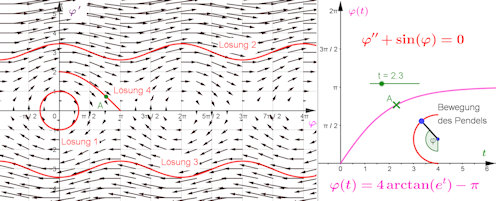
|
Abb. 4.9 Phasenraumdiagramm für ein Stangenpendel. Links ist das Phasenraumdiagramm
zu sehen. Drei besondere Lösungen sind in Mathematica gerechnet und hier eingezeichnet, weil
die analytischen Lösungen elliptische Integrale benotigen, die in GeoGebra nicht zur Verfügung
stehen. (Siehe Beispiel 4.7). Rechts ist fur die Lösung 4 die im Text angegebene Funktion
φ(t) im tφ-Koordinatensystem gezeichnet (violett). Die Zeit t kann mit dem Schieberegler
verändert werden, dann bewegt sich darauf der Punkt A = (t, φ(t)) entsprechend, der mit
A = (φ(t), φ'(t)) im linken Bild, dem Phasenraumdiagramm, gekoppelt ist. Die eingefügte
Ansicht des Stangenpendels von der Nulllage bis zum instabilen Gleichgewichtspunkt bewegt
sich auch passend mit.
|
||||||||||||
| Abschnitt 4.3.4.1 Seite 324 Auflage 1: Seite 300 Beispiel 4.7 |
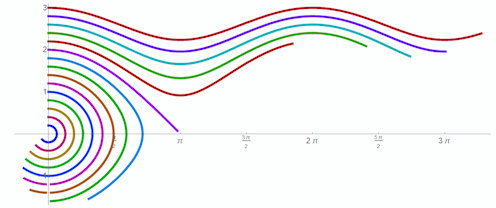
|
Abb. 4.10 Exakte Lösungen der DGL des Pendels. Gezeigt
sind Lösungen mit Anfangswerten \(\varphi(0)=0\) und \(\varphi'(0)=\omega_0\) für
\(\omega_0 = 0.2,\,0.4,\,\dots,\,3.0\). Damit beginnen die Kurven an der
senkrechten Achse im Phasenraum. Die Zeit läuft bei allen Kurven von \(t=0\) bis
\(t=4\). Die Kurven sind dennoch unterschiedlich lang, weil mit höherer
Startgeschwindigkeit das Pendel in der gleichen Zeit einen größeren
Winkelweg zurücklegt. \(\omega_0=2\) ergibt die Lösung 4.
|
||||||||||||
|
Anregung 4.3
Abschnitt 4.3.4.1 Seite 324
|
|
|||||||||||||
| Abschnitt 4.4.1 Seite 326 Auflage 1: Seite 302 |
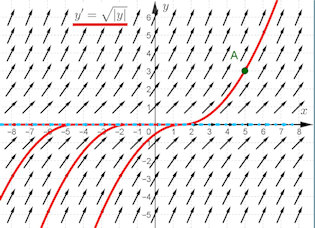
|
Abb. 4.11 DGL ist nicht eindeutig
lösbar. Durch alle Punkte gehen beliebig viele Lösungen:
die (hellblaue) spezielle Lösung \(y\equiv0\) und Kombinationen davon mit
Parabelästen unterhalb oder oberhalb der x-Achse. Vier Lösungen durch
Punkt \(A\) sind gezeigt. Den unteren Parabelast kann man noch so weit
nach rechts schieben, dass er genau an den oberen anschließt.
|
||||||||||||
| Abschnitt 4.4.1 Seite 328 Auflage 1: Seite 304 |
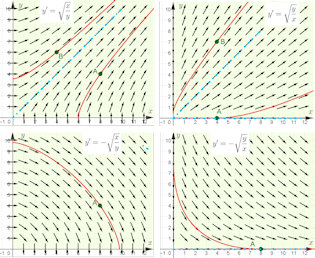
|
Abb. 4.12 Der
Definitionsbereich der DGL hat einen Rand. Der Definitionsbereich der rechten Seite der DGLn ist gelblich unterlegt. Lösungen beginnen am Rand und laufen dann evtl. bis ins Unendliche. Die speziellen Lösungen sind hellblau eingetragen. Bei den rechten Bildern sorgt \(y\equiv0\) wieder für mehrfache Lösungen durch Punkte auf der x-Achse.
|
||||||||||||
In großer Ausführlichkeit folgen im Buch die Abschnitt 4.5.1 bis 4.5.5, die das Vorgehen beschreiben und begünden. |
||||||||||||||
| Abschnitt
4.5.2 Seite 331 Beispiele 4.8 Seite 333 4.9 Seite 340 u.a. Auflage 1: Seiten 307, 309, 316 |
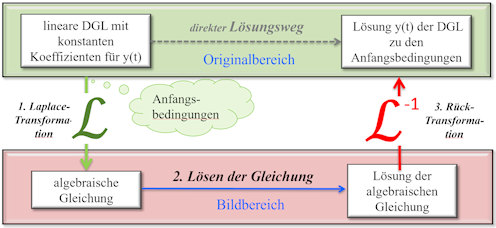
|
Abb. 4.13 Lösung einer DGL mit
Laplace-Transformation.
Grundlegendes Vorgehen. Aufgegriffen in Beispiel 4.8 Seite 333 Normale Welt \(\longrightarrow\)Laplace-Welt für \(y'' - y' -2y = 0 \mbox{ mit Anfangswerten } y(0) = 4,\ y'(0) = -1\). Aufgegriffen in Beispiel 4.9 Seite 340 Laplace-Welt \(\longrightarrow\)Normale Welt. |
||||||||||||
|
Anregung 4.4
Abschnitt 4.5.5 Seite 337
|
|
|||||||||||||
| Abschnitt 4.5.6 Seite 338 Auflage 1: Seite 314 |
|
Abb. 4.14 Bausteine für
Lösungen homogener linearer DGLn mit konstanten Koeffizienten.
Jede Zelle enthält einen Übersichtsgraphen der Funktion, die sich als Produkt
des Eintrags vor der Zeile und des Eintrags über der Spalte ergibt. Blau unterlegt sind die Fälle mit reellen Nullstellen, die für DGLn 2. Ordnung möglich sind. Es können nur entweder zwei Felder der 1. Zeile oder zwei übereinanderliegende der ersten und der zweiten Zeile Summanden der Lösung sein. Grün unterlegt sind die Fälle von DGLn 2. Ordnung mit zwei komplexen Nullstellen. Es können einzelne Zellen oder zwei übereinander stehende Zellen Summanden der Lösung sein. Es sind zu den roten Lösungsgraphen blaue "Einhüllende" gezeichnet. Die Zeile mit weißem Hintergrund kann bei mehrfachen reellen Nullstellen auch mit höheren Potenzen von \(t\) gedacht werden, aber die Ordnung der DGL muss dann um eins höher sein als der Exponent von \(t\). |
||||||||||||
| Abschnitt
4.5.11.1 Seite 347 Auflage 1: Seite 323 |
In dem Richtungsfeld Abb. 4.4 b) geht es um die DGL
\(y'(t)=y(t)+\sin t\), die in diese Kategorie gehört
und die im Buch in Abschnitt 4.5.11.1 Seite 348 auch mit Laplacetransformation gelöst wird. |
|||||||||||||
| Beispiel 4.9
Seite 340 Auflage 1: Seite 316 |
Die DGL \(y''(t)-y'(t)-2y(t)=t\) wird mit Laplacetransformation gelöst. Da sie zweiter Ordnung ist, lässt sich kein Richtungsfeld zeichnen, in dem man die die Lösung verifizieren könnte. | |||||||||||||
Zusatz in Abschnitt 4.5.7 Seite 340 Auflage 1: Seite 316 |
Wir lösen eine DGL mit Laplace, die komplizierter ist als die Beispiele im Buch, aber sich dennoch von Hand einigermaßen bequem lösen lässt. Zudem können wir die Lösungsschar in einem Richtungsfeld eintragen. \[ y'(t) = y(t) + \cos t\ {\rm e}^{\frac{1}{5}t},\quad y(0) = k. \] | |||||||||||||

|
Für das Beispiel benötigen wir diese Einträge aus der Tabelle Seite 125. Für DGLn ist es nach Seite 126 üblich, die Transformierten mit Großbuchstaben zu bezeichnen: \( y(t) \longrightarrow Y(s) \qquad\mbox{und} \qquad y'(t) \longrightarrow s\;Y(s)+ y(0) \) | |||||||||||||
| Am Ende des Kapitels 01Analysis2d bei den Integraltransformationen Abschnitt 1.9.7 haben wir hier auf der Website ausführlich an diesem Beispiel die Laplacetransformation von \(g(t)=\cos t\ {\rm e}^{\frac{1}{5}t} \) visualisiert und verständlich gemacht. |
||||||||||||||
Laplacetransformation nach der Tabelle führt auf
\[
sY(s) - y(0) = Y(s) + \frac{s-\frac{1}{5}}{\left(s-\frac{1}{5}\right)^2+1}.
\]
Auflösen nach \(Y(s)\):
\[
Y(s)(s-1) = k + \frac{s-\frac{1}{5}}{\left(s-\frac{1}{5}\right)^2+1},
\]
\[
Y(s) = \frac{k}{s-1} + \frac{s-\frac{1}{5}}{\left(\left(s -
\frac{1}{5}\right)^2+1\right)(s-1)}.
\]
Ansatz für die Partialbruchzerlegung:
\[
\frac{A}{s-1} + \frac{Cs+D}{\left(s-\frac{1}{5}\right)^2+1} =
\frac{s-\frac{1}{5}}{\left(\left(s -
\frac{1}{5}\right)^2+1\right)(s-1)}.
\]
Die Gleichung mit dem rechten Nenner multiplizieren und dann Kürzen, Klammern auflösen und nach s-Potenzen sortieren:
\[
A\left(\left(s - \frac{1}{5}\right)^2+1\right) + (Cs+D)(s-1) = s -\frac{1}{5},
\]
\[
s^2(A+C) + s\left(-\frac{2}{5}A+D-C\right) + \frac{1}{25}A+A-D = s
-\frac{1}{5}.
\]
Koeffizientenvergleich liefert die Gleichungen
\[
0 = A+C,\quad \text{also} \quad C = -A,
\]
\[
1 = -\frac{2}{5}A+D-C = \frac{3}{5}A+D,\quad \text{also} \quad D =
1-\frac{3}{5}A,
\]
\[
-\frac{1}{5} = \frac{26}{25}A-D = \frac{26}{25}A-1+\frac{3}{5}A =
\frac{41}{25}A-1,\quad \text{also} \quad
A=\frac{25}{41}\cdot\frac{4}{5} = \frac{20}{41},
\]
\[
C = -\frac{20}{41},\quad D = 1-\frac{3}{5}\cdot\frac{20}{41} = \frac{29}{41}.
\]
Damit haben wir
\[
Y(s) = \frac{k}{s-1} +\frac{20}{41}\cdot\frac{1}{s-1} +
\frac{-\frac{20}{41}s+\frac{29}{41}}{\left(s-\frac{1}{5}\right)^2+1}.
\]
Für den Zähler des letzten Bruches brauchen wir eine Gestalt, die den
linearen Term \(s-\frac{1}{5}\) enthält, wir schreiben also um:
\[
Y(s) = \left(k+\frac{20}{41}\right)\frac{1}{s-1} +
\frac{-\frac{20}{41}\left(s-\frac{1}{5}\right)-\frac{4}{41} +
\frac{29}{41}}{\left(s-\frac{1}{5}\right)^2+1}.
\]
Damit gelingt nun die Rücktransformation:
\[
y(t) = \left(k+\frac{20}{41}\right){\rm e}^t - \frac{20}{41}\cos t\
{\rm e}^{\frac{1}{5}t} + \frac{25}{41}\sin t\ {\rm e}^{\frac{1}{5}t}.
\]
Die DGL ist gelöst.
 Es ging also um die DGL \(y'(t)=y(t)+\cos(t)e^{\frac{1}{5}t}\). Links ist das Richtungsfeld dazu zu sehen, dessen Erzeugung in GeoGebra bei Abb. 4.4 erlärt ist. Anstelle des roten Terms finden Sie in der nachfolgenden Datei \(yy+\cos(xx)e^{\frac{1}{5}xx}\), denn \(s\) hat hier schon eine andere Bedeutung. Die grüne Funktion links hat den hier als Lösung gefundenen Term(t). Für die blaue Lösung durch \(A=(ax,ay)\) musste die Gleichung \(ay=Term(ay)\) nach \(k\) aufgelöst werden. Im GeoGeba-CAS verhindern Doppelbuchstaben \(kk,axx,ayy\), dass die momentanen Werte aus dem Grafikfenster genommen werden. \( \left\{ kk = \frac{41 \; ayy + 20 \; \cos\left( axx \right) \; e^{\frac{axx}{5}} - 20 \; e^{axx} - 25 \; e^{\frac{axx}{5}} \; \sin \left( axx \right)}{41 \; e^{axx}} \right\} \) Nun kann die blaue Lösung bewegt werden. |
||||||||||||||
| Abschnitt 4.5.8 Seite 341 Auflage 1: Seite 317 |
|
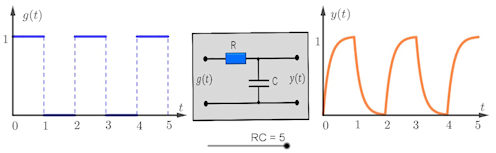
Abb. 4.15 Laplace-Transformation für einen Tiefpass.
Beispiel zur Regelungstechnik: Das Eingangssignal für einen Tiefpass
ist hier eine periodische Rechteckschwingung. Das Ausgangssignal hängt von
den Eigenschaften der Schaltelemente ab. Auf der
Website kann das Produkt \(RC\) verändert und die Wirkung
beobachtet werden.
|
||||||||||||
| Abschnitt 4.5.8.1 Seite 342 Auflage 1: Seite 318 |
|
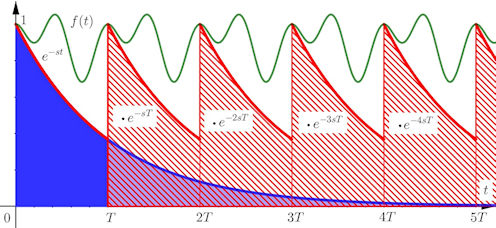
Abb. 4.16 Laplace-Transformation für eine periodische
Funktion. Zu sehen sind: grün \(f(t)\), blau \({\rm e}^{-st}\), rot die
periodische Fortsetzung von \({\rm e}^{-st}\big|_{[0,T]}\) mit Periode \(T\).
|
||||||||||||
| Abschnitt 4.5.10 Seite 418 Auflage 1: Seite 322 |
|
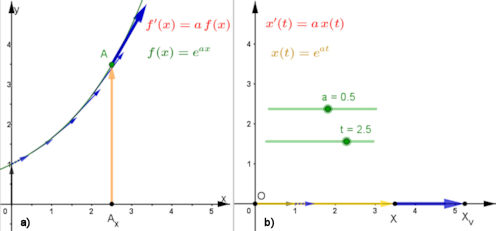
Abb. 4.18 Hinführung zur
Euler'schen Formel. a) Lösung und Deutung der DGL \(f'(x) =
a\cdot f(x)\), hier gezeigt für \(a=0.5\). Rückt \(A\) nach rechts, wird die
Ordinate immer größer. Der blaue Geschwindigkeits-Vektor hat die \(a\)-fache
Länge in Tangentenrichtung. b) Die Ordinate aus a) ist nun ein Vektor
\(\vec x(t)\) in x-Achsenrichtung und sein \(a\)-faches ist der
Geschwindigkeitsvektor \(\vec x\,'(t)\), bezeichnet als \(X_v\).
|
||||||||||||
| Abschnitt 4.5.10 Seite 347 Auflage 1: Seite 323 |
|
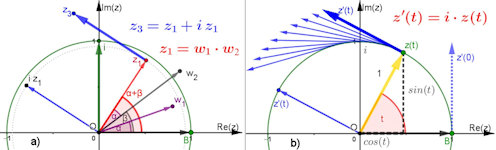
Abb. 4.19 Komplexe Zahlen als Vektoren.
a) Beim Produkt komplexer Zahlen werden die Argumente
(= Winkel) addiert und die Beträge multipliziert. Speziell bewirkt die
Multiplikation mit i eine Drehung um \(90^{\circ}\).
b) Bei der komplexen DGL \(z'(t) = \) i\(\cdot z(t)\)
ist im Vergleich mit der reellen DGL nun \(a=\) i. Die Lösung ist also
\(z(t)={\rm e}^{{\rm i} t}\).
Wie in b) hervorgehoben steht der blaue Vektor
\(z'(t)\) stets senkrecht auf \(z(t)\), daher wird \(z(t)\) nicht
länger und wegen |i| = 1 verlängert sich auch der
blaue Vektor nicht.
|
||||||||||||
| Abschnitt 4.6.1 Seite 350 Auflage 1: Seite 326 Beispiel 4.10 |
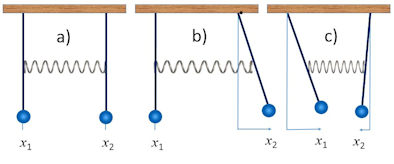
|
Abb. 4.20 Gekoppelte Pendel als Stangenpendel,
verbunden durch eine Feder.
a) Ruhezustand, b) Anfangsbedingung mit Auslenkung des rechten Pendels, c) Zustand einige Zeit nach dem Loslassen des rechten Pendels. Die Lage der Koordinaten \(x_1\) und \(x_2\) ist eingezeichnet. |
||||||||||||
| Abschnitt 4.6.1 Seite 352 Auflage 1: Seite 328 |
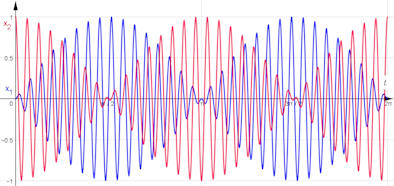
|
Abb. 4.21 Lösungskurven zu
gekoppelten Pendeln.
Die Amplituden beider Pendel verändern sich mit der Zeit selbst sinusförmig. |
||||||||||||
| Abschnitt 4.6.3 Seite 356 Auflage 1: Seite 332 |
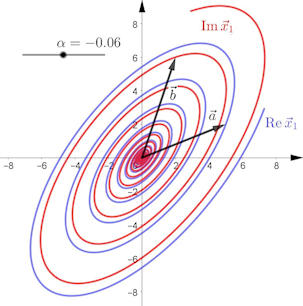
|
Abb. 4.22 Lösungen zu
komplexen Eigenwerten. Gezeigt wird als Beispiel ein 2-dimensionales System,
daher spannen die Vektoren
\(\vec a\) und \(\vec b\) den ganzen Raum auf. Am Schieberegler kann der Realteil
\(\alpha\) des Eigenwertes verändert werden.
\(\alpha=-0.06\) sorgt für ein langsames
Schrumpfen, führt aber zu krummen Werten in der
Matrix \(A\). Für den interessierten Leser sollen die Details dieses Systems von
DGLn genannt werden: Die Matrix ist
\(A = \frac{1}{650}\left(\begin{smallmatrix}
-589 & 725 \cr -1000 & 511
\end{smallmatrix}\right)\).
Es sind dann die Eigenvektoren \(\vec v_{1,2} = (5\pm2{\rm i},2\pm6{\rm i})^{\rm T}\), also
\(\vec a = (5,2)^{\rm T},\ \vec b = (2,6)^{\rm T}\), zu Eigenwerten
\(\lambda_{1,2} = -0.06\pm{\rm i}\).
| ||||||||||||
| Abschnitt 4.6.3 Seite 356 Auflage 1: Seite 332 |
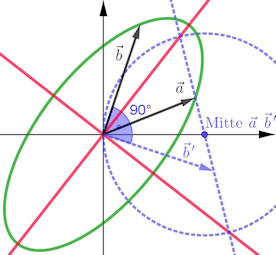
|
Abb. 4.23 Ellipse als spezielle
Lösung. Die Haupt- und Nebenachsen der Ellipse sind eingezeichnet.
Die Konstruktion der Achsen aus den Vektoren \(\vec a\) und \(\vec b\)
nach David Rytz ist in blau eingezeichnet: Man konstruiert \(\vec b\,'\)
senkrecht auf \(\vec b\) und schlägt dann den Kreis um die Mitte von \(\vec a\) und
\(\vec b\,'\) durch den Ursprung. Diesen schneidet man mit der Geraden durch die
Endpunkte von \(\vec a\) und \(\vec b\,'\).
|
||||||||||||
|
Anregung 4.5
Abschnitt 4.6.3 Seite 358
|
|
|||||||||||||
| Abschnitt
4.6.4 Seite 359 und zu Beispiel 4.11 Abschnitt 4.6.3 Seite 357 Auflage 1: Seiten 333 und 337 |
a)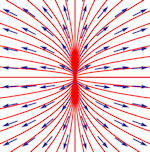 b)
b)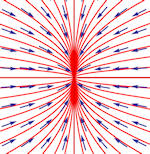 c)
c)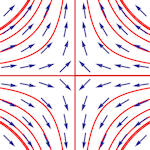
d) 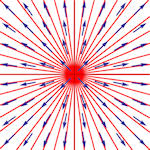 e)
e) f)
f)
g)  h)
h) i)
i)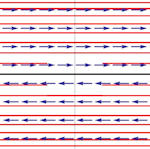
j)  k)
k) l)
l)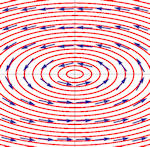
m)  n)
n)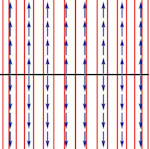 o)
o)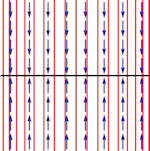
|
Tabelle 4.3 Lösungeskurven zu zweidimensionalen Systemen.
Umfassende Übersicht. Die zugehörigen Matrizen und Eigenwerte finden Sie im Buch. Auch die Dimension des Eigenraumes wird betrachtet. Anmerkung: Wenn Sie auf eins der Bilder klicken, erscheint es in neuem Tab vergrößert und gibt seinen sprechenden Namen preis. Beipiel 4.11 Auf Seite 357 zeigt eine ergänzende Rechnung zum Teilbild i). |
||||||||||||
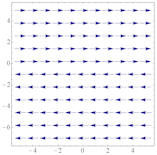
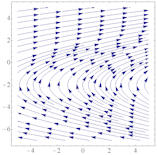
| Abschnitt 4.6.5 Seite 363 Auflage 1: Seite 339 |
|
Abb. 4.24 Vergleich
homogenes und inhomogenes System von DGLn.
Links sind Richtungsvektoren des homogenen,
rechts Lösungen des inhomogenen Systems mit \(a=2\) und \(b=1\)
zu sehen. Die Geraden parallel zur x-Achse
im homogenen Fall schließen sich im inhomogenen zu Parabeln zusammen.
|
||||||||||||
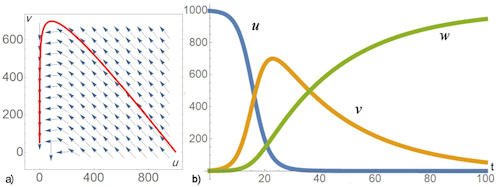
| Abschnitt 4.6.6 Seite 364 Auflage 1: Seite 340 |
|
Abb. 4.25 System von DGLn für eine
Epidemie. a) Phasenraumdiagramm für \(u\) und \(v\) mit der Lösung zu den Anfangswerten \(\beta = 0.0004,\ \gamma = 0.035,\ u(0)=997,\ v(0)=3\), b) Entwicklung der Epidemie mit Lösungskurven für \(u(t),\ v(t),\ w(t)\). |
||||||||||||
| Abschnitt 4.6.6 Seite 365 Auflage 1: Seite 341 |

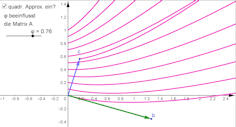
|
Abb. 4.26 Verlauf von Lösungskurven außerhalb von Fixpunkten. Die
Lösungskurven zu
\(\vec x\,' = A\vec x + \vec b\) werden links in linearer,
rechts in quadratischer
Näherung gezeigt. Die Matrix \(A\) ist eine Drehungsmatrix mit Drehwinkel
\(\varphi\). Anfangspunkt \(\vec c\) und Vektor \(\vec b\) können verschoben werden.
|
||||||||||||
| Zusatz |
Diese Datei bietet die Möglichkeit, das Richtungsfeld zum DGl-System darzustellen und die exakte Lösung durch den Punkt \(\vec c\) anzuzeigen. Dann kann man verfolgen, dass die linearen Approximationen zu den Lösungen wirklich mit den richtigen Steigungen beginnen, und dass die quadratischen Approximationen im Startpunkt auch die richtige Krümmung haben.
Zwar liegt im Ursprung kein Fixpunkt vor - so war das System konstruiert worden -, aber das schließt Fixpunkte an anderer Stelle nicht aus. Tatsächlich gibt es einen Fixpunkt, der eingezeichnet ist. Auch das Richtungsfeld zeigt dort ein typisches Verhalten. Um welche Art von Fixpunkt handelt es sich? Probieren Sie auch andere Winkel \(\varphi\) für die (Dreh-)Matrix \(A\) aus. Die Lage des Fixpunkts hängt davon und von \(\vec b\) ab. Insbesondere für \(\varphi=0^\circ\) ergibt sich ein strahlenförmiges Richtungsfeld, so dass die Lösungen wirklich exakte Geraden sind. Der Fixpunkt liegt dann bei \(-\vec b\). Wird andererseits \(\vec b=\vec0\) gesetzt, so landet der Fixpunkt im Ursprung. Die Rechnungen zur Bestimmung der erstaunlich komplizierten Lösungen stehen in den folgenden Notebooks: |
|||||||||||||
| Abschnitt 4.6.6 Seite 366 Auflage 1: Seite 342 |
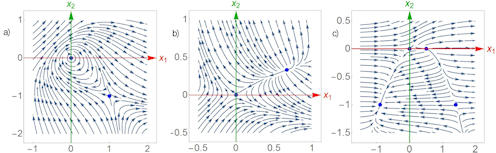
|
Abb. 4.27 Nichtlineare DGL-Systeme.
a)} Wirbel und instabiler Knoten, b)} Instabiler Knoten und instabiler Fixpunkt, c)} Instabiler und stabiler Knoten und zwei instabile Fixpunkte. |
||||||||||||
| Abschnitt 4.7.2 Seite 369 Auflage 1: Seite 345 |
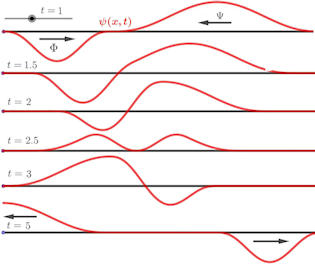
|
Abb. 4.29 Lösung
für eine schwingende Saite. Die Lösung \(\psi(x,t) = \Phi(x-ct)
+ \Psi(x+ct)\) besteht aus zwei verschieden großen Wellenbergen, einer
positiv, der andere negativ, die sich in entgegengesetzter Richtung bewegen.
Die Teilbilder zeigen das Verhalten der Lösung zu aufeinanderfolgenden
Zeitpunkten.
ANIMIERT |
||||||||||||
| Abschnitt 4.7.3 Seite 370 Auflage 1: Seite 346 |
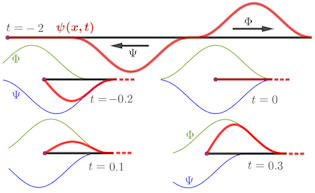
|
Abb. 4.30 Lösung für eine schwingende eingespannte Saite. Die Lösung
\(\psi(x,t) = \Phi(x-ct) + \Psi(x+ct)\) besteht aus einem Wellenberg \(\Phi\) und seiner
Punktspiegelung \(\Psi\), die sich in entgegengesetzter Richtung bewegen. Die
Teilbilder zeigen das Verhalten der Lösung an einem Ende der Saite zu
aufeinanderfolgenden Zeitpunkten. Die Summanden \(\Phi\) und \(\Psi\) sind
grün bzw. blau dazu gezeichnet.
|
||||||||||||
| Abschnitt 4.8.1 Seite 373 |
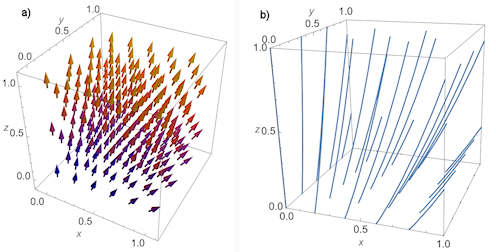
|
Abb. 4.31 Vektorfeld zu einer quasilinearen PDGL 1. Ordnung.
Als Beispiel dient die PDGL \(x u_x +y u_y = 2u + 1.\) a) zeigt das
Vektorfeld, b) die dazu gehörigen charakteristischen Kurven.
|
||||||||||||
| Abschnitt 4.8.2 Seite 373 |
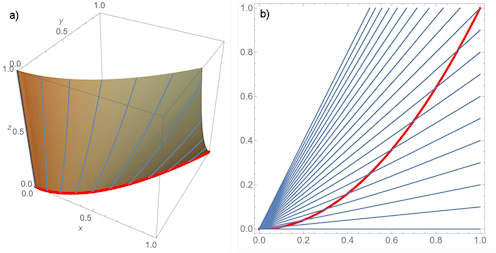
|
Abb. 4.32 Lösung über einer vorgegebenen Kurve.
a) zeigt die Lösung mit den darin enthaltenen charakteristischen Kurven,
b) projiziert diese in die xy-Ebene, so entstehen die
Charakteristiken. Die vorgegebene Kurve \(\gamma\) ist
in beiden Bildteilen rot.
|
||||||||||||
| Abschnitt 4.8.3 Seite 376 |
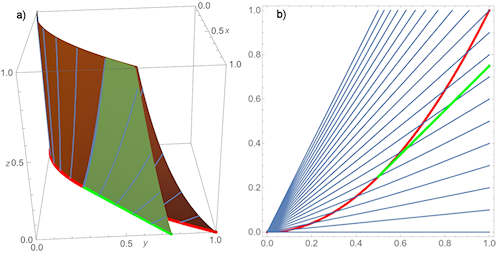
|
Abb. 4.33 Zusammengesetzte Lösung.
a) die neue angefügte Lösung ist grün. Sie findet sich auch in
b) in der Projektion auf die xy-Ebene in grün wieder.
|
||||||||||||
| Abschnitt 4.8.3 Seite 378 |
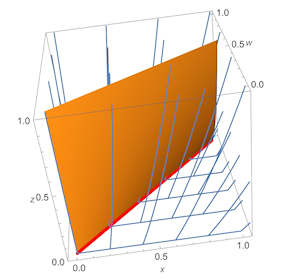
| ../../../NeuauflageBilder/Notebooks Geogebra für neue Bilder/PDGLVektorfeldCharKur.nb
Abb. 4.34 Die Lösung nach Einführung der Charakteristiken als neue Koordinate.
Das Bild zeigt die Lösung zu unserem Beispiel und zur gleichen Vorgabe,
aber nun in xw-Koordinaten. Die projizierten charakteristischen Kurven, also die neuen Charakteristiken, sind gegeben durch \(w=\text{const}\). Die Cauchy-Bedingungen lauten jetzt \(v(x,w) = 0\) auf \((x,w) = \bar\gamma(s) = (s,s)\). \(\bar\gamma(s)\) ist wieder in rot eingezeichnet. |
||||||||||||
| Abschnitt 4.9.3 Seite 384 |
|
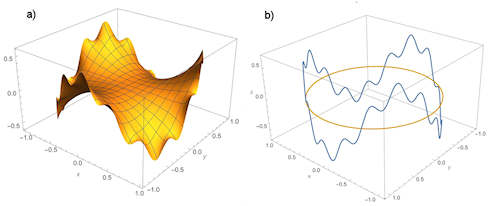
Abb. 4.35 Lösung der Laplace-Gleichung auf dem Einheitskreis.
a) Die Lösung \(u(x,y)\),
b) dazu die Vorgabe über dem Einheitskreis.
|
||||||||||||
| Abschnitt 4.9.3 Seite 385 |
|
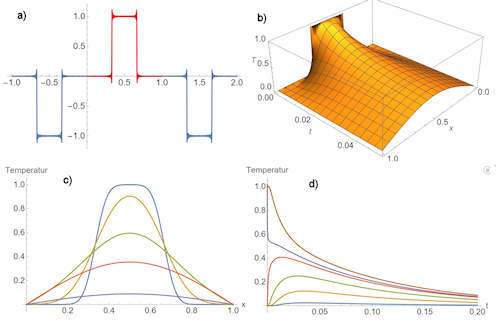
Abb. 4.36 Lösung der Wärmeleitungsgleichung.
a) \(f(x)\) approximiert
durch eine Fourierreihe mit 200 Summanden, b) die Lösung \(u(x,t)\) dazu daraus berechnet, c) der Temperaturverlauf von oben nach unten zu den Zeiten \(t=0.001,0.005,0.02,0.06,0.2\), und d) der Temperaturverlauf von unten nach oben an den Stellen \(x=0.02,0.1,0.2,0.3,0.34,0.5\). |
||||||||||||
|
|||||||