ISBN 978 662 69291 2 Auflage 2 Book Springer Spektrum
ISBN 978 662 69292 9 Auflage 2 eBook
www.mathematik-sehen-und-verstehen.de
https://masuv.web.leuphana.de (Sicherer Zugang)
Dieter Riebesehl
Hubert Dammer |
Höhere Mathematik sehen und verstehen
ISBN 978 662 69291 2 Auflage 2 Book Springer Spektrum ISBN 978 662 69292 9 Auflage 2 eBook www.mathematik-sehen-und-verstehen.de https://masuv.web.leuphana.de (Sicherer Zugang) |
Dörte Haftendorn Dieter Riebesehl Hubert Dammer |
|
Lösungen der Anregungen in Kapitel 4
 |
||||
| Anr. 4.1 Kettenlinie | Anr. 4.2 Schwingung | Anr. 4.3 StangenPendel | Anr. 4.4 komp. Nullst. | Anr. 4.5 Systeme-2-Dimensional |
| Anregung 4.1
Abschnitt 4.3.2.1 Seite 315 |
4.1 DGL der Kettenlinie
Versuchen Sie doch einmal, die DGL der Kettenlinie \(y'' = k \sqrt{1 + (y')^2}\) zu lösen. Hinweis Es reichen die beiden genannten Tricks: - die Substitution ist \(z(x) = y'(x)\) - und eine gute Formelsammlung. |
Lösung zu 4.1
Mit der im Hinweis angegebenen Substitution ist \(y'' = z'\), damit sehen die DGL und die weitere Rechnung wie folgt aus: \begin{align*} z' &= \sqrt{1+z^2} \\ \frac{{\rm d}z}{\sqrt{1+z^2}} &= k{\rm d}z & (*) \\ {\rm arsinh}z &= kx + C \\ y' = z &= \sinh(kx + C) & (**) \\ y(x) &= \frac{1}{k}\cosh(kx + C) \end{align*} Die Richtigkeit der Schritte (*) und (**) prüft man nach, indem man umgekehrt die Ableitungen der angegebenen Stammfunktionen mit der Tabelle in Abschnitt 1.6.1.3 auf Seite 56 ausrechnet. |
| Anregung 4.2
Abschnitt 4.3.4.1 Seite 322 |
4.2 Gedämpfte Schwingungen
Versuchen Sie doch einmal, auf der Website die verschiedenen Sonderfälle durch geschickte Wahl von \(\delta\) und \(\omega_0\) zu erreichen. Es gibt: 1. eine sich aufschaukelnde Schwingung für \(\delta < 0\), 2. die ungedämpfte Schwingung mit \(\delta = 0\), 3. eine gedämpfte Schwingung mit \(0<\delta<\omega_0\), 4. den aperiodischen Grenzfall mit \(\delta = \omega_0\), bei dem sich \(x\) asymptotisch der Null nähert und keine Schwingung auftritt, 5. einen Kriechfall für \(\omega_0<\delta\) ohne Schwingungen für noch größere Dämpfung. Lösungen 4. und 5 4. \(\delta = 0.8,\ \omega_0 = 0.8\) 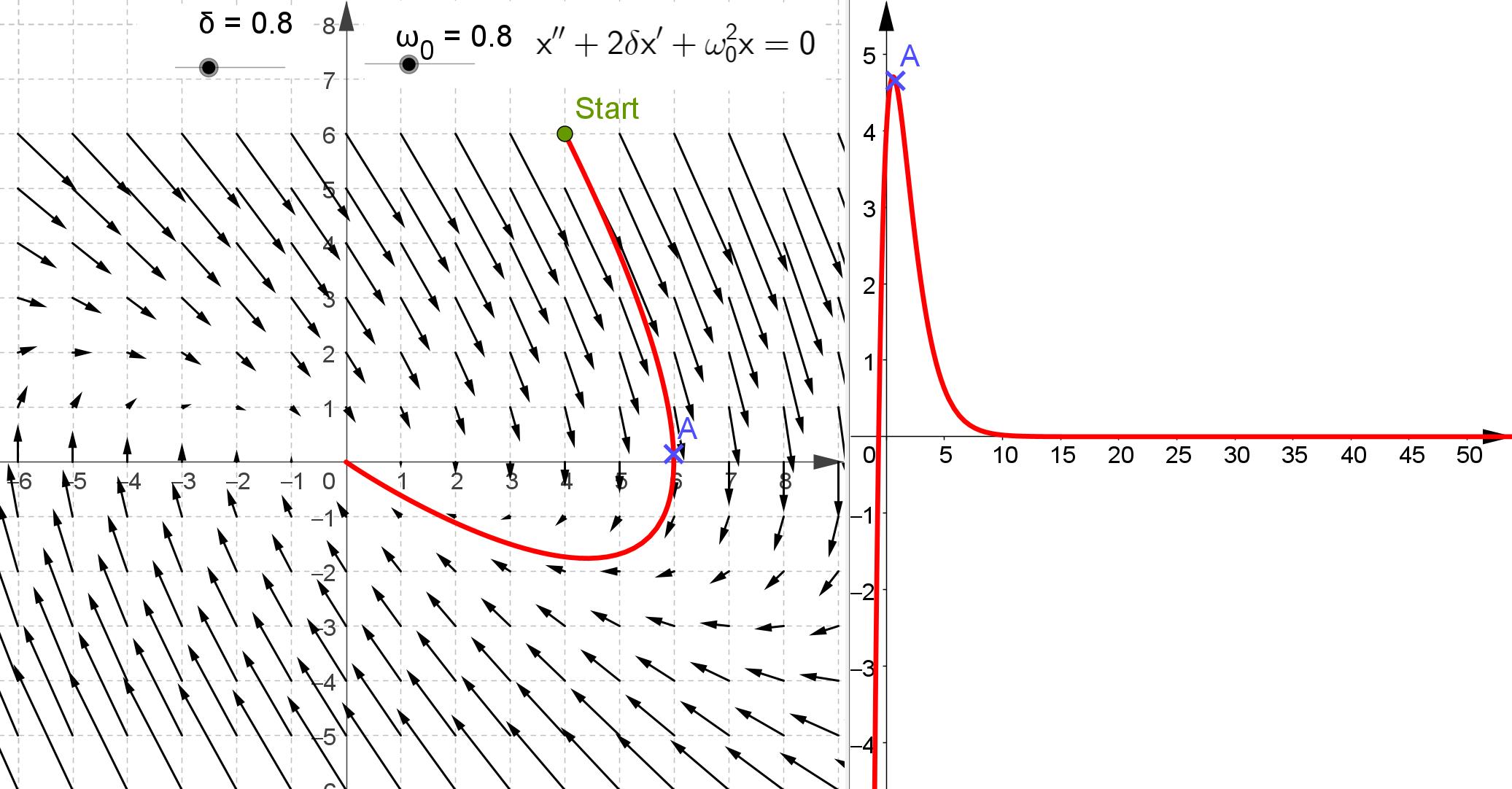 5. \(\delta = 2,\ \omega_0 = 0.8\)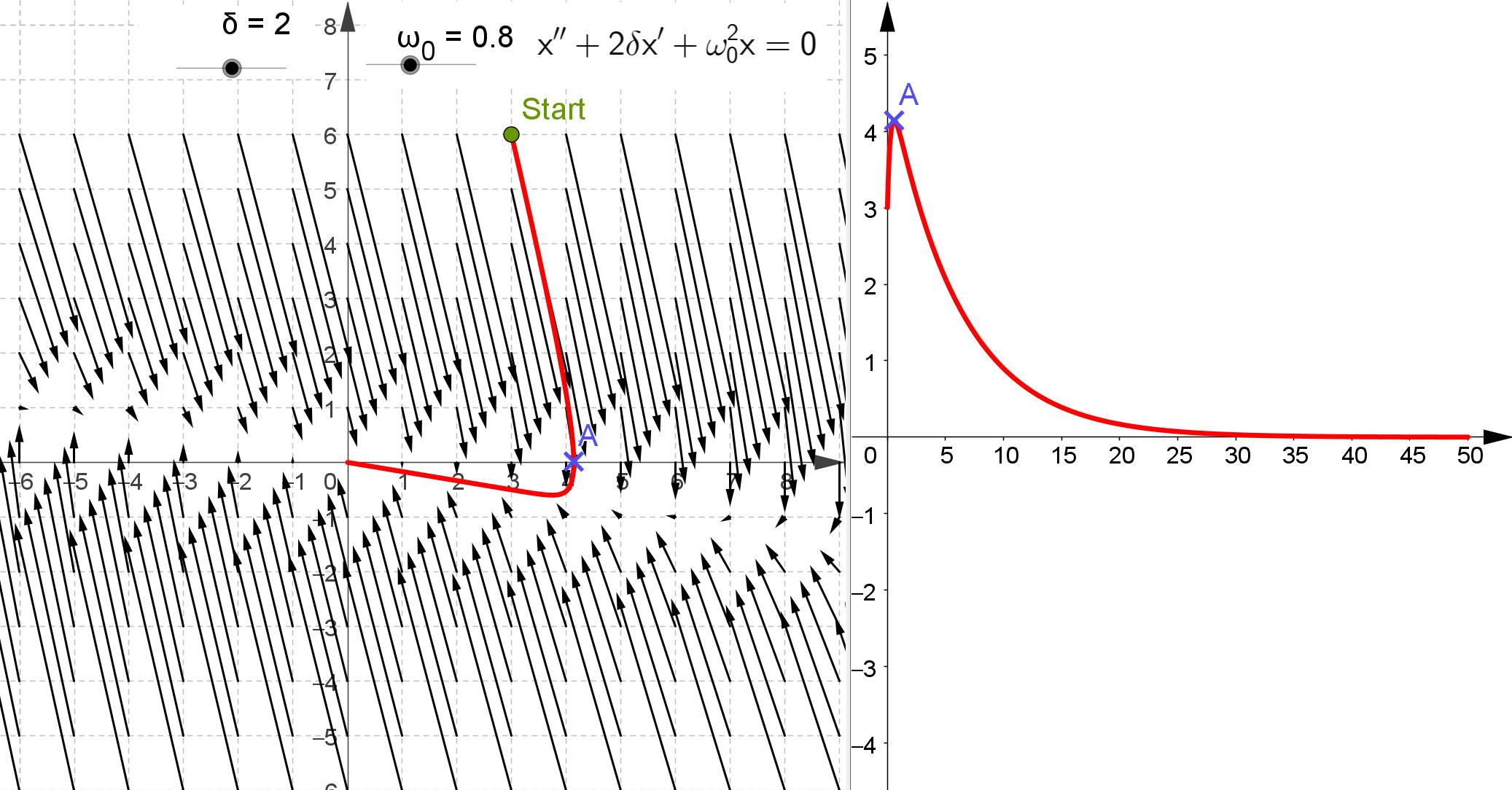 
|
Lösung zu 4.2
Hier ist ja klar, was zu tun ist. Für alle Leser, die keinen Zugriff auf Geogebra haben oder die einfach nur das Ergebnis sehen wollen, zeigen wir hier die Bilder für alle fünf Fälle. 1. \(\delta = -0.1,\ \omega_0 = 0.8\) 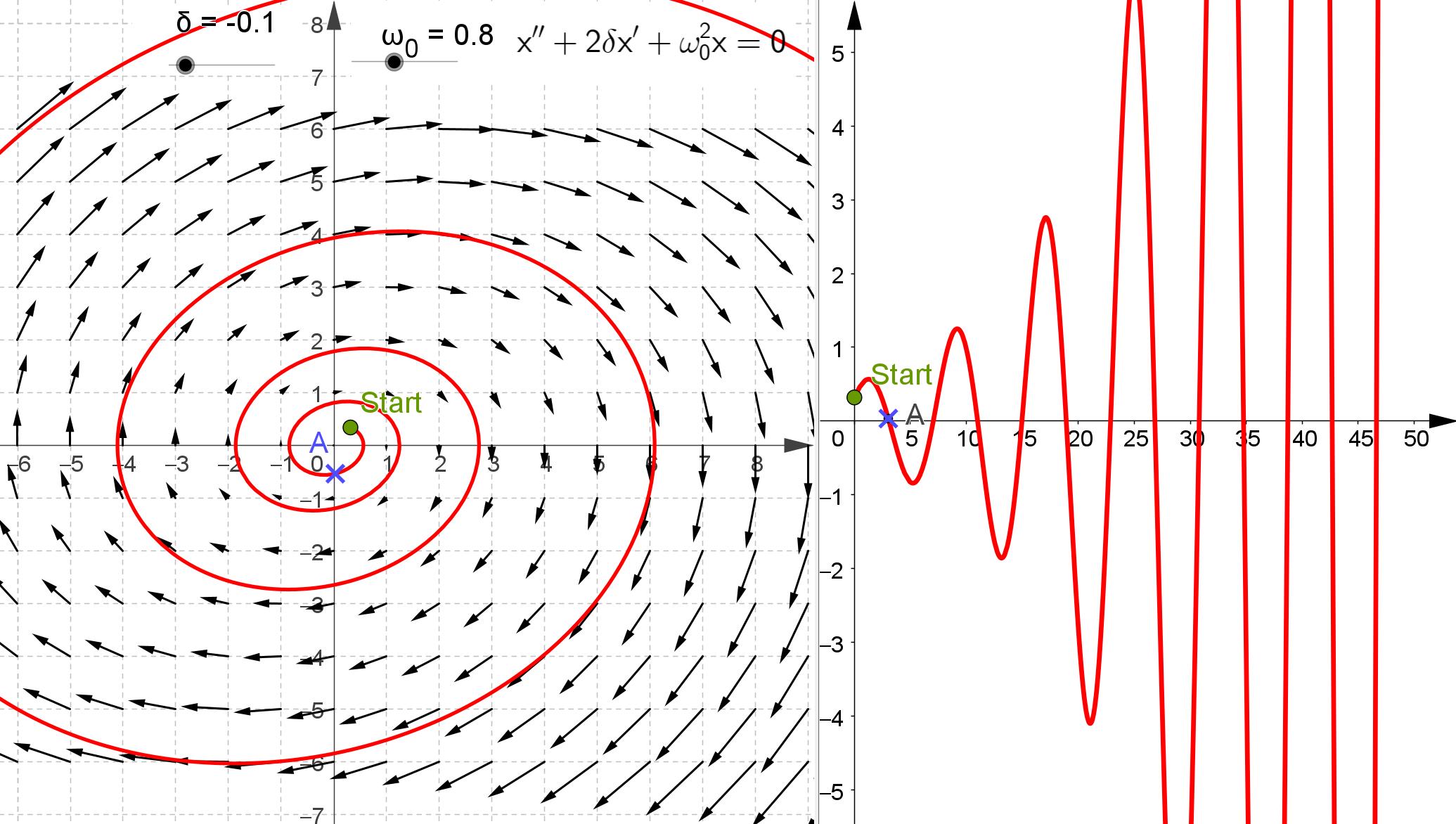 2. \(\delta = 0,\ \omega_0 = 0.8\) 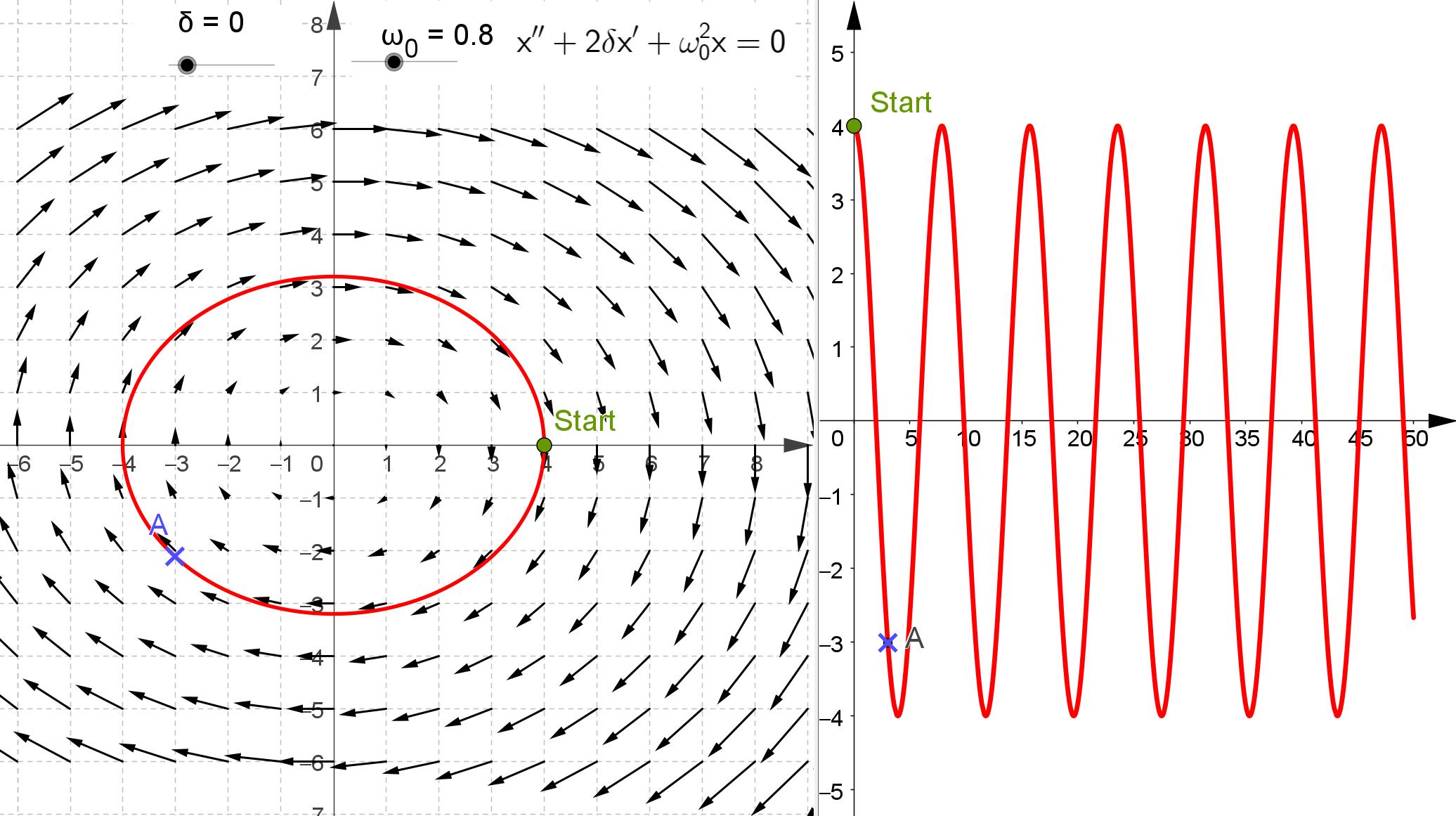 3. \(\delta = 0.1,\ \omega_0 = 0.8\)  |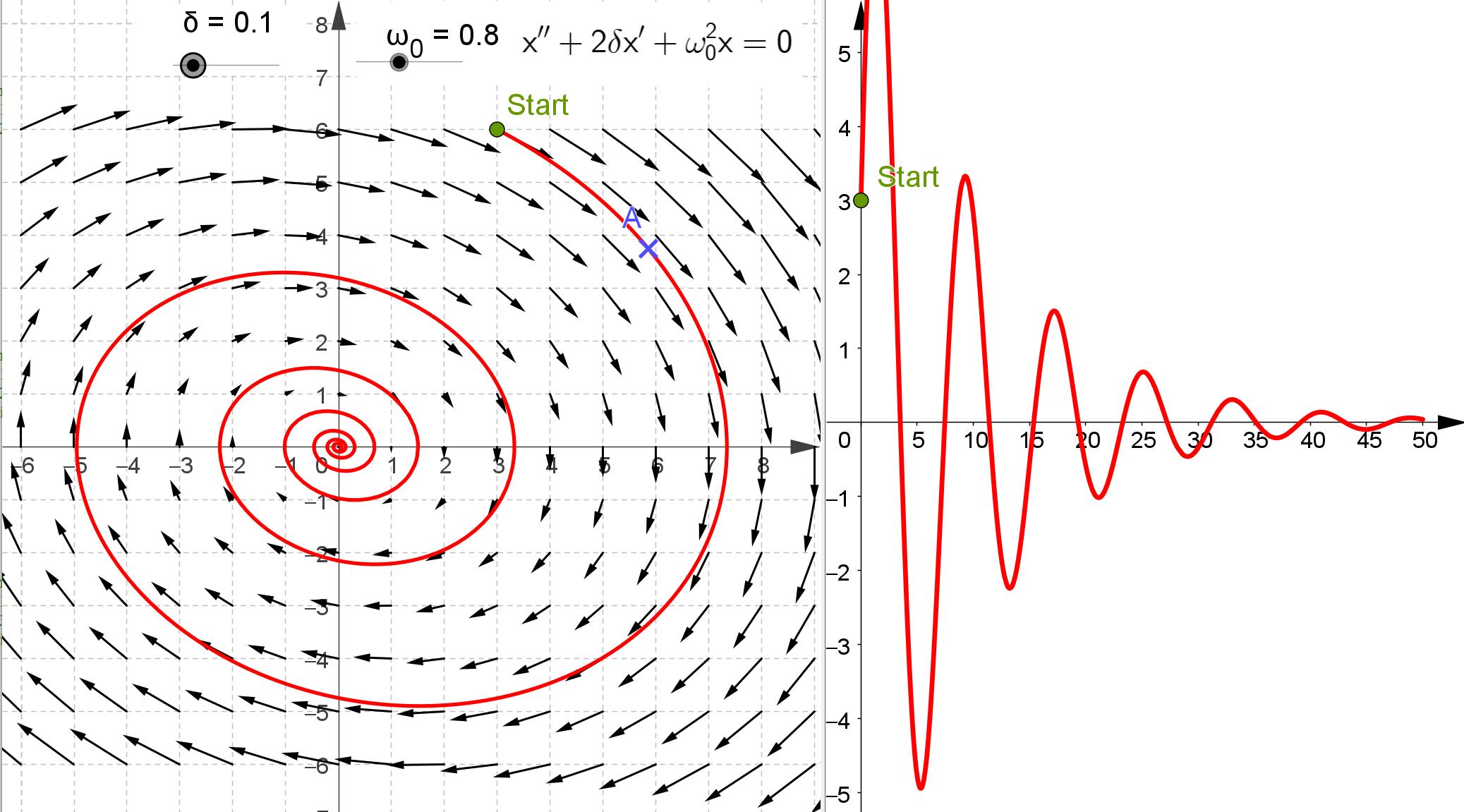
|||
| Anregung 4.3
Abschnitt 4.3.4.1 Seite 324 |
4.3 Zum Verständnis des Stangenpendels
Der Leser versuche sich klarzumachen, dass die in Mathematica gerechneten und in Abb. 4.9 eingetragenen Lösungen folgende Situationen zeigen: Lösung 1: Normal schwingendes Pendel mit kleiner Auslenkung. Lösung 2: Überschlagendes Stangenpendel, das sich ewig weiter dreht. Lösung 3: Überschlagendes Stangenpendel, aber in Gegenrichtung. Lösung 4: Pendel mit exakt so viel Schwung aus der Ruhelage angestoßen, dass es genau bis zum Ãœberschlagspunkt kommt und dort im Kopfstand stehenbleibt (instabiles Gleichgewicht). Ordnen Sie dann die in Abb. 4.10 gezeigten Lösungen diesen vier Kategorien zu. |
Lösung zu 4.3
Wir zeigen noch einmal Abb. 4.10, aber diesmal mit anderen Farben: Grün: Lösung 2 Rot: Lösung 4 Blau: Lösung 1 Lösung 3 kommt nicht vor.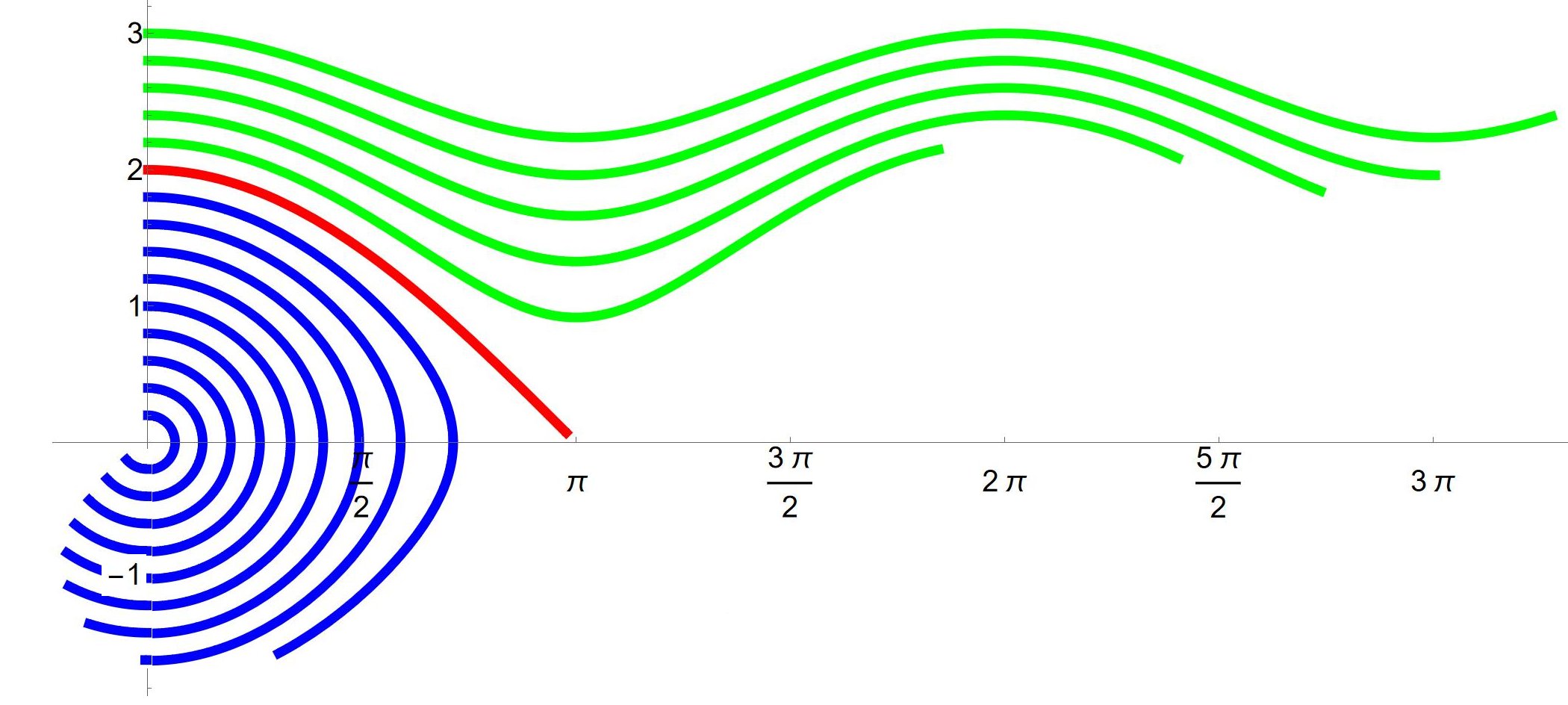 
|
|||
| Anregung 4.4
Abschnitt 4.5.5 Seite 337 |
4.4 Laplace mit komplexen Nullstellen
Lösen Sie die DGL \(y'' + y = 0\) mit Anfangswerten \(y(0) = 2,\ y'(0) = -2\) mit Hilfe einer Laplace-Transformation. |
Lösung zu 4.4
Die Laplacetransformation \(\cal L\) überführt die DGL in \[ s^2Y(s) -2s +2 + Y(s) = 0 \] mit der Lösung \[ Y(s) = \frac{2s-2}{s^2+1} = \frac{2s}{s^2+1} - \frac{2}{s^2+1}. \] 1. Der direkte kürzere Weg benutzt benutzt die letzten beiden Einträge aus der Tabelle in Abschnitt 4.5.5 auf Seite 336 mit \(a=0\) und \(\omega_0 = 1\) zur Rücktransformation \(\cal L^{-1}\): \[ y(t) = 2\cos(t){\rm e}^{-0t} - 2\sin(t){\rm e}^{-0t} = 2(\cos(t) - \sin(t)). \] 2. Der Weg über die komplexen Nullstellen des Nenners benötigt eine Partialbruchzerlegung: \[ Y(s) = \frac{2s-2}{s^2+1}= \frac{2s-2}{(s+{\rm i})(s-{\rm i})} = \frac{A}{s+{\rm i}} - \frac{B}{s-{\rm i}}. \] Für die Zähler erhält man die Gleichung \(2s-2 = (A+B)s + {\rm i}(B-A)\), Koeffizientenvergleich ergibt \[ A+B = 2,\quad B-A = 2{\rm i} \] mit den Lösungen \[ B = 1+{\rm i},\quad A = 1-{\rm i}. \] Der dritte Eintrag aus der Tabelle in Abschnitt 4.5.5 auf Seite 336 mit \(a=-{\rm i}\) bzw. \(a={\rm i}\) ergibt die Rücktransformation \(\cal L^{-1}\): \begin{align*} y(t) &= (1-{\rm i}){\rm e}^{-{\rm i}t} + (1+{\rm i}){\rm e}^{{\rm i}t} = \\ &= (1-{\rm i})(\cos t - {\rm i}\sin t) + (1+{\rm i})(\cos t + {\rm i}\sin t) = \\ &= 2\cos t - 2\sin t + {\rm i}(-\cos t - \sin t + \cos t + \sin t) = \\ &= 2(\cos(t) - \sin(t)). \end{align*} |
|||
| Anregung 4.5
Abschnitt 4.6.3 Seite 358s |
4.5 Basislösungen zu mehrfachen Eigenwerten
Versuchen Sie, für die Beispiele g) und h) aus Tabelle 4.3, Seite 360, zu den Matrizen \(A=\left(\begin{smallmatrix}1&1\\ 0&1\end{smallmatrix}\right)\) bzw. \(A=\left(\begin{smallmatrix}-1&-1\\ 0&-1\end{smallmatrix}\right)\), die auf Seite 361 angegebenen Basislösungen \(\vec x_2(t)=\left(\begin{smallmatrix} t\\ 1\end{smallmatrix}\right){\rm e}^t\) bzw. \(\vec x_2(t)=\left(\begin{smallmatrix} -t\\ 1\end{smallmatrix}\right){\rm e}^{-t}\) selbst zu finden. |
Lösung zu 4.5
h) Die Matrix \(A\) hat den doppelten Eigenwert \(\lambda = -1\), der Eigenraum dazu ist 1-dimensional mit Eigenvektor \(\vec v_1=\left(\begin{smallmatrix}1\\ 0\end{smallmatrix}\right)\). Er liegt im Kern von \(A-\lambda E=\left(\begin{smallmatrix}0&-1\\ 0&0\end{smallmatrix}\right)\). Wir suchen einen weiteren linear unabhängigen Vektor aus dem Kern von \((A-\lambda E)^2=\left(\begin{smallmatrix}0&0\\ 0&0\end{smallmatrix}\right)\), ein solcher ist \(\vec v_2=\left(\begin{smallmatrix}0\\ 1\end{smallmatrix}\right)\). Die zweite Eigenlösung errechnet sich dann wie folgt: \[ \vec x_2(t)=(\vec v_2+t(A-\lambda E)\vec v_2){\rm e}^{-t} = \left(\left(\begin{smallmatrix} 0\\ 1\end{smallmatrix}\right) + t\left(\begin{smallmatrix} -1\\ 0\end{smallmatrix}\right)\right){\rm e}^{-t} = \left(\begin{smallmatrix} -t\\ 1\end{smallmatrix}\right){\rm e}^{-t}. \] |
|||
|
|||||||
 Prof. Dr. Dörte Haftendorn
| Prof. Dr. Dieter Riebesehl
| Dipl.-Math. Dipl.-Ing. Hubert Dammer
|
|||||
