 5.1 Numerische Fehler
5.1 Numerische Fehler
|
Abschnitt
5.1.2
Seite 389
Auflage 1:
5.1.1.1
Seite 351

|
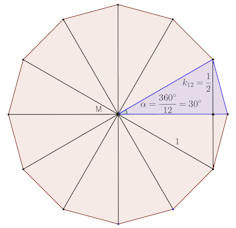 Iteration für \(\pi\)
Iteration für \(\pi\)
Seitenzahl: \(n=12\)
Segmenthöhe: \(k_n=0.5\)
Vieleckfläche: \(\displaystyle A_n=\frac{n}{2}k_n=3\)
|
Verdopplung:
\(k_{2n} = \) \(\displaystyle\sqrt\frac{1-\sqrt{1-k_n^2}}{2}\),
\(A_{12\cdot2^m} =
3\cdot2^m\stackrel{\mbox{ \(m+1\) Wurzeln}}{\sqrt{2 - \sqrt{2+\sqrt{2+\dots\sqrt{3}}}}}\)
\(\xrightarrow{m\to\infty}\pi\) für \(m\ge1\)
 Zwölfeck.ggb
Zwölfeck.ggb
|
Abschnitt
5.1.2
Seite 389
Auflage 1:
5.1.1.1
Seite 351
|
|
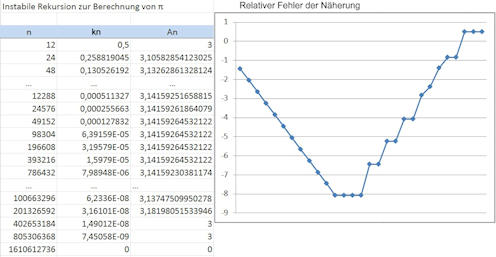
Abb. 5.1 Iterative Berechnung
von \(\pi\). In der Excel-Tabelle sind ein paar Zeilen ausgelassen. In
der rechten Grafik ist aber für alle Zeilen der erreichte relative
Fehler der Näherung für \(\pi\) aufgezeichnet. An der y-Achse stehen die
dekadischen Logarithmen des relativen Fehlers, also z.B. \(-4\) für \(10^{-4}\).
 ApproximationPi.xlsx
ApproximationPi.xlsx
|
Abschnitt
5.1.2
Seite 390
Auflage 1:
5.1.1.1
Seite 352
|
|
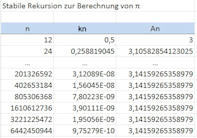
Abb. 5.2 Stabile
iterative Berechnung von \(\pi\).
\(n\) ist die Eckenzahl der regelmäßigen
\(n\)-Ecke aus der 12-Eck-Familie,
\(k_n\) sind die Höhen der Segmente,
\(A_n\) ist die Gesamtfläche des \(n\)-Ecks, die im Grenzwert für \(n\to\infty\)
gerade \(\pi\) sein muss.
Nur der Anfang und der Schluss der
Rechnung sind gezeigt.
 ApproximationPi.xlsx
ApproximationPi.xlsx
|
 5.2 Nullstellensuche
5.2 Nullstellensuche
|
 5.2.1 Bisektion
5.2.1 Bisektion
|
Abschnitt
5.2.1
Seite 391
Auflage 1:
Seite 353

|
|
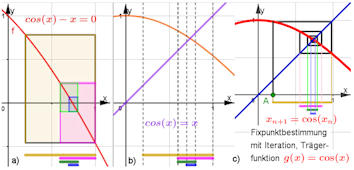
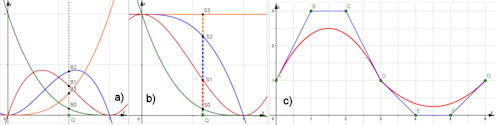
Abb. 5.3 Intervallschachtelungen.
Bei allen Verfahren ist unten eine Intervallschachtelung angegeben,
In a) und b) wird sie durch fortgesetzte Halbierung,
Bisektionen, gefunden. c) zeigt die Lösung des Problems mit einer
rekursiven Folge zur Fixpunktgleichung \(\cos x = x\), siehe
Abschnitt 5.2.4.
 bisektion.ggb
bisektion.ggb
|
 5.2.2 Sekantenverfahren
5.2.2 Sekantenverfahren
|
Abschnitt
5.2.2
Seite 392
Auflage 1:
Seite 354

|
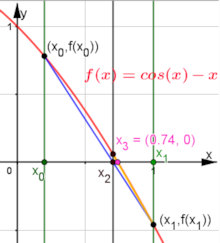
|
Abb. 5.4 Sekantenverfahren. Neue Näherung \(x_2\)
ist die Nullstelle der Sekante durch die Graphenpunkte an den Enden des
Intervalls \([x_0,x_1]\). Mit einfacher Rechnung und \(y_i=f(x_i)\), \(i=0,1\),
ergibt sich
\[
x_2 =\frac{y_0 x_1-y_1 x_0}{y_0-y_1}.
\]
Das neue Intervall ist \([x_0,x_2]\) oder \([x_2,x_1]\), je nachdem, welches
Vorzeichen \(f(x_2)\) hat. Man sieht hier, dass man für die Funktion
\(f(x) = \cos x - x\) und Start bei \(x_0=0.2,\ x_1=1\), mit \(x_3=0.74\)
schon 2-stellige Genauigkeit der Nullstelle
erreicht hat.
 sekanten-verfahren.ggb
sekanten-verfahren.ggb
|
 5.2.3 Newtonverfahren
5.2.3 Newtonverfahren
|
Abschnitt
5.2.3
Seite 393
Auflage 1:
Seite 355

|
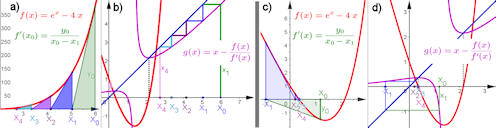
|
Abb. 5.5 Nullstellensuche mit dem Newtonverfahren für
\(f(x) = {\rm e}^x-4x\).
Es sind je zwei gekoppelte
Grafikfenster nebeneinander dargestellt. Links
ist jeweils der Funktionsgraph und die definierende Tangentenfolge, rechts
die Trägerfunktion der Newton-Iteration mit der Folge der Näherungspunkte
zu sehen. a) und b) zeigen ein "übliches" Beispiel, bei dem die
Näherungsfolge monoton fallend auf die gesuchte Nullstelle zuläuft.
c) und d) zeigen einen anderen Ausschnitt derselben Funktion. Damit
erklären sich einige Überraschungen, die man mit der Newton-Iteration erleben
kann. Der Text geht darauf in Abschnitt 5.2.4.2 ein.
 newton_it-DH1.ggb
newton_it-DH1.ggb
 newton_it-DH2.ggb
newton_it-DH2.ggb
 newton_it-DH3.ggb
newton_it-DH3.ggb
|
Abschnitt
5.2.4.1
Seite 395
Auflage 1:
Seite 357

|
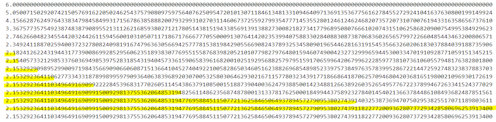
|
Abb. 5.6 Wie schnell
konvergiert das Newtonverfahren? Man misst die
Konvergenzgeschwindigkeit
daran, mit welchem Faktor die Anzahl der richtig berechneten Stellen von
Schritt zu Schritt wächst. Hier werden die gelben Balken, die dies anzeigen,
bei jedem Schritt etwa doppelt so lang.
|
Abschnitt
5.2.4.2
Seite 396
Auflage 1:
Seite 358

|
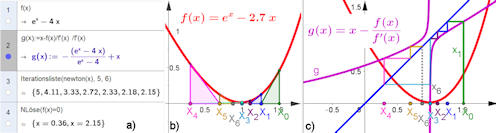
|
Abb. 5.7 CAS mit GeoGebra und
Überraschung beim Newtonverfahren. a) zeigt die Berechnung der
Trägerfunktion des Newtonverfahrens und die Berechnung von Folgenwerten. In
b) und c) sind wieder zwei
gekoppelte Grafikfenster nebeneinander
dargestellt, aber diesmal für die Nullstelle von \({\rm e}^x-2.7x\).
Betrachtet man nur berechnete Folgenglieder, ohne auf einen
Graphen zu achten, könnte man meinen, die Folge konvergiere gegen einen Wert
zwischen \(x_3\) und \(x_6\). In c) erkennt man aber, dass die
rekursive "Treppchenfolge" überhaupt nicht konvergieren wird. Ein Zoom im
Fenster b) hätte auch gezeigt: Es gibt gar keine Nullstelle.
 newton-it-cas1.ggb
newton-it-cas1.ggb
 newton-it-cas2.ggb
newton-it-cas2.ggb
 newton-it-cas4.ggb
newton-it-cas4.ggb
|
 5.2.4 Heron-Verfahren
5.2.4 Heron-Verfahren
|
Abschnitt
5.2.5.1
Seite 397
Auflage 1:
Seite 359

|
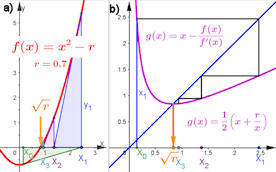
|
Abb. 5.8 Das Heronverfahren als Rekursion.
a) zeigt eine Parabel mit der Nullstelle \(\sqrt{r}\), die mit dem
Newtonverfahren approximiert wird. b)
verfolgt mit dem Startwert \(x_0\) die Heronfolge im gekoppelten Fenster in der
iterativen Treppendarstellung. Wenn Sie in GeoGebra
\(x_0\) oder den Radikanden \(r\) verändern, reagieren beide Darstellungen
gemeinsam. In Bild b) ist die Trägerfunktion eine Hyperbel.
 heron-newton_it.ggb
heron-newton_it.ggb
|
| |
Anregung 5.1
Abschnitt
5.3.5.1
Seite 397

|
|
Anregung 5.1 (Heron-Verfahren für höhere Wurzeln) |
|
Ein Vorschlag für eine Verallgemeinerung des Heronverfahrens zur Berechnung
von \(\sqrt[k]r\) ist die Rekursion
\( x_{n+1}=\frac{1}{2}\left(x_n+\frac{r}{x_n^{k-1}}\right)\).
Berechnen Sie den Fixpunkt und untersuchen Sie die Konvergenz bzw. Divergenz.
Erhält man dasselbe, wenn man stattdessen wieder mit dem Newtonverfahren
arbeitet?
Variieren Sie in der GeoGebra-Datei obigen das \(k\)
und sehen Sie sich die Entwicklung der Treppchen an.
|
|
|
 5.3 Interpolation und Kurven gestalten
5.3 Interpolation und Kurven gestalten
|
 5.3.1 Interpolation mit Poynomen
5.3.1 Interpolation mit Poynomen
|
Abschnitt
5.3.1.2
Seite 400
Auflage 1:
Seite 362

|
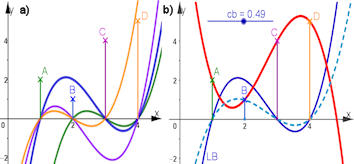
|
Abb. 5.9 Interpolation nach Lagrange.
a) zeigt Lagrange-Basis-Polynome, die an genau 3 Stützstellen
Nullstellen haben.
In b) wird z.B. der Faktor \(c_b\) für
\(L_B(x)\) gefunden, der \(L_B\) so staucht, dass \(B\) auf dem Graphen liegt.
Das rote Interpolationspolynom entsteht auf diese Weise.
 LagrangePolynome.ggb
LagrangePolynome.ggb
|
Abschnitt
5.3.1.2
Seite 401
Auflage 1:
Seite 363

|
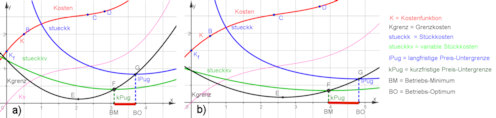
|
Abb. 5.10 Kostenfunktion als
Lagrange-Polynom, aus ihr wird alles, was noch dargestellt ist, berechnet.
Erfahren Sie durch Ziehen an den gegebenen Punkten,
wie überraschend deutlich die Wirtschaftsaussagen, die sich daraus ergeben,
auf kleine Änderungen der Lage reagieren.
 lagrange_wirtschaft3.ggb
lagrange_wirtschaft3.ggb
|
Abschnitt
5.3.1.3
Seite 402
Auflage 1:
Seite 364

|
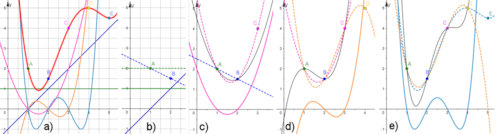
|
Abb. 5.11 Das Newton'sche-Interpolations-Polynom ist eine Linearkombination der Newton'schen
Basispolynome, die aus immer mehr Linearfaktoren \((x-\mbox{Stützstelle})\)
aufgebaut sind und mit den passenden Koeffizienten immer mehr Stützpunkte
genau treffen.
 newton_interpolation.ggb
newton_interpolation.ggb
|
 5.3.2 Interpolation mit kubischen Splines
5.3.2 Interpolation mit kubischen Splines
|
Abschnitt
5.3.2
Seite 403
Auflage 1:
Seite 365

|
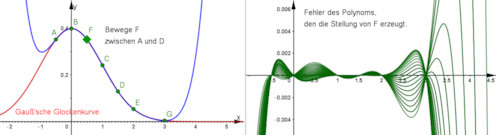
|
Abb. 5.12 Gauß'sche
Glockenkurve und Interpolationspolynom. a) Die Punkte \(A,\,\dots,\,G\) liegen
auf der Glockenkurve, das blaue Interpolationspolynom passt nach
Sicht brauchbar in deren Bereich.
b) Wie gut die Passung wirklich ist, sieht man
durch Visualisierung der Differenzen zur Glockenkurve. für verschiedene
Stellungen von \(F\) zwischen \(A\) und \(G\) ist je eine solche "Fehlerkurve"
gezeichnet.
 interpol-gauss-deutlich.ggb
interpol-gauss-deutlich.ggb
|
 5.3.3 Kurvengestaltung mit Bézier-Splines
5.3.3 Kurvengestaltung mit Bézier-Splines
|
Abschnitt
5.3.2.1
Seite 404
Auflage 1:
Seite 366

|
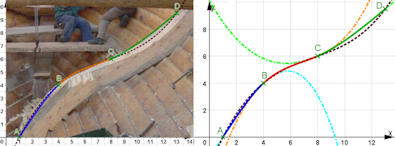
|
Abb. 5.13 Poeler Kogge und Splines.
Einsatz von Splines (drei durchgezogene bunte Stücke) für die Balkenform der
Kogge, die Nägel sind in den Punkten \(A,B,C,D\)
zu denken.
Leider kann man die Punkte (noch) nicht ziehen, weil wir die Koeffizienten aus einer Berechnung mit Mathematica übertragen haben.
Später kann man dann selbst ein anderes Bild hinterlegen.
 poelerkogge3.ggb
poelerkogge3.ggb
|
Abschnitt
5.3.2.2
Seite 405
Auflage 1:
Seite 367

|
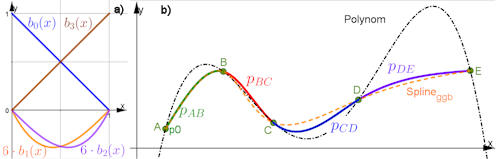
|
Abb. 5.14 Basisfunktionen für
kubische Splines.
Links: \(b_0,\ b_3\), und 6-fach überhöht \(b_1,\ b_2\).
Rechts: Ein damit erstellter nat ürlicher Spline durch 5 Nägel, in vier
Farben durchgezogen dargestellt. Die Nägel
sind frei verschiebbar. Zum Vergleich ist das
Interpolationspolynom schwarz gestrichelt dazu gezeichnet. Man sieht, dass der
Spline wesentlich weniger "ausschwingt". Orange gestrichelt ist das Ergebnis
des GeoGebra-Befehls Spline(A,B,C,D,E), siehe dazu den Text.
 BasisKubSplinesNatuerl.ggb
BasisKubSplinesNatuerl.ggb
 SplineKub5Punkte.ggb
SplineKub5Punkte.ggb
|
 Abschnitt 5.3.2.2 Abschnitt 5.3.2.2
Seite 406
Auflage 1:
Seite 368
|
Hier finden Sie die Ableitungen der Spline-Basisfunktionen und die Herleitung der Gleichungen zur Splineberechnung.
Zunächst tabellarisch die Basisfunktionen und deren Ableitungen an den Intervallenden 0 und 1:
\[
\begin{array}{|l|l|l|l|}
\hline
b_0(x) = 1 - x & b'_0(x) = -1 & b'_0(0) = -1 & b'_0(1) = -1 \\
\hline
b_1(x) = \frac{1}{6}(1-x)(x-2)x & b'_1(x) = \frac{1}{6}\left((2-x)x
+ (1-x)x + (1-x)(2-x)\right) & b'_1(0) = -\frac{1}{3} & b'_1(1) =
\frac{1}{6} \\
\hline
b_2(x) = \frac{1}{6}(x-1)(x+1)x & b'_2(x) = \frac{1}{6}\left((x+1)x
+ (x-1)x + (x-1)(x+1)\right) & b'_2(0) = -\frac{1}{6} & b'_2(1) =
\frac{1}{3} \\
\hline
b_3(x) = x & b'_3(x) = 1 & b'_3(0) = 1 & b'_3(1) = 1 \\
\hline
\end{array}
\]
Die im Punkt \(B\) zusammentreffenden Splinepolynome sind mit den Bezeichnungen aus dem Buch
\( p_{AB} = A_y b_0^{AB} + c_A b_1^{AB} + c_B b_2^{AB} + B_y b_3^{AB} \quad \) und
\( \quad p_{BC} = B_y b_0^{BC} + c_B b_1^{BC} + c_C b_2^{BC} + C_y b_3^{BC} \).
Die Bedingung einer stetigen 1. Ableitung im Punkt \(B\) führt zu \( p_{AB}'(B) = p_{BC}'(B).\)
Hier setzt man die oben angegebenen Ableitungen ein und nutzt aus, dass \( b_i^{BC} \) einfach das nach rechts
verschobene \( b_i^{AB} \) ist:
\( A_y b_0'(1) + c_A b_1'(1) + c_B b_2'(1) + B_y b_3'(1) =
B_y b_0'(0) + c_B b_1'(0) + c_A b_2'(0) + C_y b_3'(0)\)
\( -A_y + \frac{1}{6}c_A + \frac{1}{3}c_B + B_y =
-B_y - \frac{1}{3}c_B - \frac{1}{6}c_A + C_y \)
\( \frac{1}{6}c_A + \frac{2}{3}c_B + \frac{1}{6}c_C = C_y - 2B_y + A_y\)
\( \frac{1}{6}(c_A + 4c_B + c_C) = C_y - 2B_y + A_y\)
Das ist die erste der Gleichungen, die anderen ergeben sich daraus durch Verschiebung zu den nächsten Punkten.
|
Abschnitt
5.3.3
Seite 407
Auflage 1:
Seite 369

|
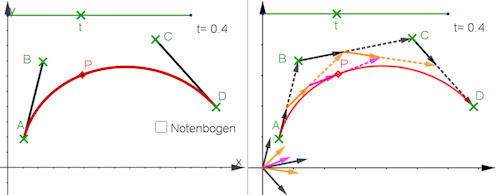
|
Abb. 5.15 Bézierkurve a)
zusammen mit ihren Steuerpunkten \(A,B,C,D\), in
b) erzeugt aus ihrem "Gerüst": Man wählt einen
Prozentsatz \(t\) zwischen 0 und 1, hier \(t=0.4=40\%\),
und markiert auf jedem der schwarzen Gerüstvektoren den \(40\%\)-Punkt von \(A\),
von \(B\) und von \(C\) aus. Auf den zwei sich daraus ergebenden Vektoren (orange)
werden wieder die \(40\%\)-Punkte markiert. Im nächsten Schritt (rosa) hat man
so den Punkt \(P\) der Bézierkurve erzeugt. Diese ist der geometrische Ort von
\(P\) bei jeder Wahl von \(t\). Siehe auch
Abb. 5.16 und Seite 372.
 bezier_Geruest.ggb
bezier_Geruest.ggb
|
Abschnitt
5.3.3.1
Seite 408
Auflage 1:
Seite 370

|
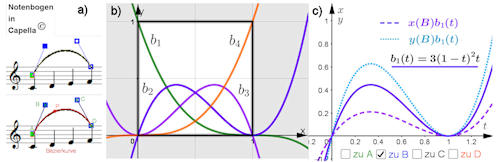
|
Abb. 5.16 Bézierkurve als
Parameterkurve mit Bernstein-Polynomen. a) zeigt den
Bézierspline, mit dem man einen Notenbogen anpassen kann,
siehe Abb. 5.15 und Seite 410.
b) Die vier Bernstein-Polynome sind eine Basis
für den Polynomraum \(\Pi_3\), wir verwenden sie im Intervall [0,1].
c) zeigt, wie die Koordinaten von \(B\) als
Koeffizienten von \(b_1\) in der Parameterkurve wirken.
 bezier_parameterkurve-summanden-buch.ggb
bezier_parameterkurve-summanden-buch.ggb
|
Abschnitt
5.3.3.2
Seite 409
Auflage 1:
Seite 371

|
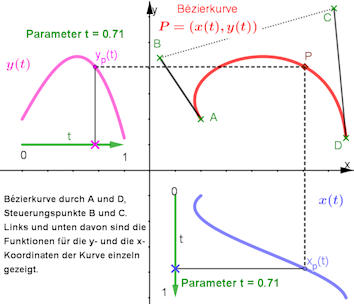
|
Abb. 5.17 Bézierkurve als
Parameterkurve.
Allgemeine Erklärung für Parameterkurven.
Die Koordinaten eines Kurvenpunktes \(P\) sind Funktionen \(x(t),\ y(t)\) eines
Parameters \(t\).
Diese beiden Funktionen sind hier zusätzlich dargestellt, und zwar so, dass
die Parameterkurve durch die waagerechten und senkrechten gestrichelten
Linien geometrisch entstehen kann.
Sie können an \(t\) ziehen, damit \(P\) wandern lassen, aber
auch das "Gerüst" verändern.
 Bezier anschaulich.ggb
Bezier anschaulich.ggb
|
Abschnitt
5.3.3.3
Seite 410
Auflage 1:
Seite 372

|
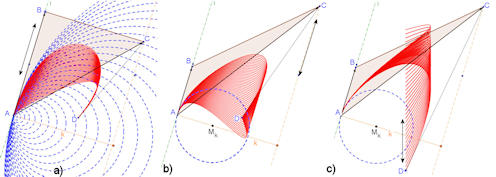
|
Abb. 5.18 Krümmung des
Béziersplines in \(A\), dargestellt durch den blauen
Krümmungskreis, mit seiner Spur in GeoGebra.
a) zeigt, dass sich bei Verlängerung von
\(\overrightarrow{AB}\) die Krümmung ändert.
In b) ändert sich die Höhe \(k\) des Dreiecks \(ABC\) nicht, wenn \(C\) auf
der Parallelen zu \(AB\) wandert, also bleibt die Kr ümmung gleich.
c) zeigt beispielhaft, dass eine beliebige Veränderung von \(D\) keinen
Einfluss auf die Krümmung in \(A\) hat.
 Bezier-kruemmung.ggb
Bezier-kruemmung.ggb
|
 Abschnitt 5.3.3.3 Abschnitt 5.3.3.3
Seite 410
Auflage 1:
Seite 372
|
Die Krümmungsformel für den Beziérspline im Punkt \(A\) lautet
\[ \kappa = \frac{2k}{3\Big|\Big|\overrightarrow{AB}\Big|\Big|} \]
mit der Höhe \(k\) auf der Seite \(AB\) im Dreieck \(ABC\).
Die Herleitung benutzt die Formel
\[
\kappa = \frac{\ddot y\dot x - \ddot x \dot y}{(\dot x^2 + \dot y^2)^{\frac{3}{2}}}.
\]
Sie ist anzuwenden auf die Parameterdarstellung
\[
\vec P = \begin{pmatrix} P_x \cr P_y\end{pmatrix},\quad
\begin{array}{cccccc}
&P_x(t)=&A_x b_0(t)&+\;B_x b_1(t)&+\;C_x b_2(t)&+\;D_xb_3(t) = x(t),\\
&P_y(t)=&A_y b_0(t)&+\;B_y b_1(t)&+\;C_y b_2(t)&+\;D_yb_3(t) = y(t),
\end{array}
\]
oder ausgeschrieben
\[
\vec P = \begin{pmatrix} x(t) \cr y(t)\end{pmatrix} = \vec A (1-t)^3 + 3\vec B (1-t)^2 t + 3\vec C (1-t)t^2 + \vec D t^3.
\]
Wir rechnen die nötigen Ableitungen im Punkt \(A\), also für \(t=0\)
aus. Dabei nehmen wir von vornherein nur Terme mit, die keinen Faktor
\(t\) enthalten, da sie ohnehin wegfallen. Bei der Anwendung der
Produktregel schreiben wir also nur die Terme auf, in denen alle
\(t\)-Faktoren "wegdifferenziert" wurden:
\[
\begin{pmatrix} \dot x(t) \cr \dot y(t)\end{pmatrix}\Bigg|_{t=0} =
\Big(-3\vec A (1-t)^2 + 3\vec B(1-t)^2\Big)\Big|_{t=0} = 3\vec B - 3\vec A.
\]
Vorsicht: für die zweiten Ableitungen müssen wir wieder auf \(\vec P\)
schauen, weil nun auch \(\vec C\) einen Beitrag leisten wird:
\[
\begin{pmatrix} \ddot x(t) \cr \ddot y(t)\end{pmatrix}\Bigg|_{t=0} =
\Big(6\vec A (1-t) - 12\vec B(1-t) + 6\vec C(1-t)\Big)\Big|_{t=0} =
6\vec C - 12\vec B + 6\vec A.
\]
\(\vec B\) hat einen Faktor 12 statt 6, weil wir bei diesem Summanden bei
Anwendung der Produktregel offenbar einmal den \(t\)-Faktor und einmal
den \((1-t)\)-Faktor ableiten müssen, aber dafür gibt es zwei
Reihenfolgen, die bei der zweimaligen Anwendung der Produktregel auch
beide vorkommen.
Wenn Sie diesem Argument nicht folgen können, dann müssen Sie alles
"zu Fuß" nachrechnen.
Nun ist alles in die Krümmungsformel einzusetzen:
\[
\kappa = \frac{3(B_x-A_x)\cdot6(A_y-2B_y+C_y) -
3(B_y-A_y)\cdot6(A_x-2B_x+C_x)}
{\big( 9(B_x-A_x)^2 + 9(B_y-A_y)^2 \big)^{\frac{3}{2}}} =
\frac{18}{27}\frac{B_xC_y + A_xB_y - A_xC_y - B_yC_x - A_yB_x +
A_yC_x}
{\Big|\Big|\overrightarrow{AB}\Big|\Big|^3}.
\]
Jetzt kommt die Dreieckshöhe \(k\) ins Spiel. Die Fläche des Dreiecks
\(ABC\) errechnet sich zu
\(\frac{1}{2}k\Big|\Big|\overrightarrow{AB}\Big|\Big|\), das Doppelte
davon ist aber gerade die Fläche des von \(\overrightarrow{AB}\) und
\(\overrightarrow{BC}\) aufgespannten Parallelogramms. Letztere lässt
sich aber auch als
\(\Big|\overrightarrow{AB}\times\overrightarrow{BC}\Big|\) schreiben.
Dieses Kreuzprodukt hat einen Wert, der sich als Determinante
mal einen Einheitsvektor \( \vec e_{\bot} \)schreiben lässt, welcher
auf der Ebene, die von \(ABC\) aufgespannt wird, senkrecht steht:
\[
\overrightarrow{AB}\times\overrightarrow{BC} =
\begin{vmatrix}
B_x-A_x & C_x-B_x \cr B_y-A_y & C_y-B_y
\end{vmatrix}\cdot\vec e_{\bot},
\]
was ausmultipliziert genau den obigen Zähler für \(\kappa\) ergibt!
Damit hat man
\[
\kappa = \frac{2}{3}\frac{k\Big|\Big|\overrightarrow{AB}\Big|\Big|}
{\Big|\Big|\overrightarrow{AB}\Big|\Big|^3} =
\frac{2}{3}\frac{k}
{\Big|\Big|\overrightarrow{AB}\Big|\Big|^2}
\]
|
 5.3.4 Bézier-Raumflächen
5.3.4 Bézier-Raumflächen
|
Abschnitt
5.3.4
Seite 411
Auflage 1:
Seite 373

|
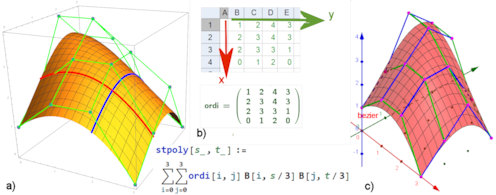
|
Abb. 5.19 Bézierfläche, erzeugt aus
ihrem "Gerüst":
a) Realisierung in Mathematica.
b) für
die Realisierung in GeoGebra nennt man im Tabellenfenster die z-Ordinaten für
die Stützpunkte. Daraus wird eine Matrix \(ordi\) erzeugt, auf deren
Komponenten man mit Indizes zugreifen kann. In griffiger Mathematica-Syntax
ist in b) unten gezeigt, wie daraus mit den Bernsteinpolynomen die
z-Komponente der Parameterdarstellung erzeugt wird. Sie ist ein Polynom 6.
Grades in s und t.
c) Realisierung im 3D-Fenster von GeoGebra.
zu a)  BezierFlaechen.nb,
Mathematica Quelltext
BezierFlaechen.nb,
Mathematica Quelltext
 Dies zum Lesen und Verstehen
Dies zum Lesen und Verstehen
|
| |
zu b) und c)  bezier-flaeche+geruest.ggb
bezier-flaeche+geruest.ggb
Anmerkung: Die Funktion Oberfläche(s,t,z(s,t),s,0,3,t,0,3) geht
stets verloren beim Öffnen. Laden Sie die ggb herunter und öffnen Sie sie dann von Hand im geöffneten GeoGebra.
Kopieren Sie von hier \(1+s-s^2/3-s^3/27+t+t^2/3-(s t^2)/3+(2 s^3 t^2)/81-(4 t^3)/27+(2 s t^3)/27-(s^2 t^3)/81-(2 s^3 t^3)/729\)
Tragen Sie diesen Term als z(s,t) in den Oberfläche-Befehl in die Eingabezeile ein.
Dann entsteht Abb. 5.19 c).
Leider ist dies nur statisch. Wenn Sie aber stpoly (steht im Algebafenster) anstelle von z eintragen,
können Sie mit unserer Datei können Sie dynamisch
experimentieren.
Leider bleibt dies nicht beim Speichern erhalten.
Die lange Summe f von oben, aber auch die für stpoly gemäß Abb. 5.19 b), lässt sich in
GeoGebra schlecht eintippen. Man erzeugt sie besser in einem anderen Editor (wir nahmen Mathematica) und überträgt
das mit Copy und Paste.
Wir haben dieses merkwürdige Verhalten dem GeoGebra-Team berichtet.
|
 5.4 B-Splines und NURBS
5.4 B-Splines und NURBS
|
 5.4.1 Bézier-Spline breiter
5.4.1 Bézier-Spline breiter
|
Abschnitt
5.4.1
Seite 412
Auflage 1:
5.4
Seite 374

|
|
Abb. 5.20 Legende Bernsteinpolynome
3. Grades, wie sie für
Béziersplines verwendet werden.
a) als Graphen,
b) gestapelt, ihre Summe ist \(=1\) für jedes \(t\)
im Intervall \([0,\,1]\),
c) Erweiterung mit drei weiteren Steuerpunkten und einer weiteren
Bézierkurve: die Gesamtkurve ist i.A. an der Nahtstelle nicht differenzierbar.
 bernsteinSumme.ggb
bernsteinSumme.ggb
|
 5.4.2 B-Splines
5.4.2 B-Splines
|
 5.4.2.1 Rekursiver Aufbau der Basen für B-Splines
5.4.2.1 Rekursiver Aufbau der Basen für B-Splines
|
Abschnitt
5.4.2.1
Seite 414
Auflage 1:
Seite 376

|
|
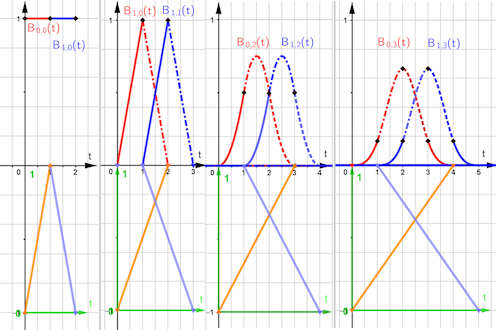
Abb. 5.21 Aufbau der Basen für B-Splines.
In der oberen Reihe sehen Sie
rote Basisfunktionen mit wachsendem Polynomgrad, die blauen entstehen aus den
roten jeweils durch Verschiebung um 1 nach rechts. Aus diesen beiden wird durch
Gewichtung mit den darunter gezeichneten Geraden als Summe die nächste rote
Basisfunktion gebildet. Dabei dient die orangefarbene Gerade als Gewicht für die
rote, die hellblaue als Gewicht für die blaue Kurve. Die neue rote Basisfunktion hat
ein um 1 breiteres Definitionsintervall.
Sie wird wieder durch Verschiebung in blau gedoppelt.
a)
Oben sind zwei Basissplines zu \(p=0\), unten haben die Geraden stets
ein angepasstes Definitionsintervall und einen Wertebereich von 0 bis 1.
b) Rote Basisfunktion zu \(p=1\) mit Verschiebung in Blau.
So geht es weiter, für c) gilt \(p=2\), in d) ist \(p=3\).
Zwei GeoGebra-Dateien (links,rechts)
 B-Spline-Basis1.ggb B-Spline-Basis1.ggb

 B-Spline-Basis2.ggb
B-Spline-Basis2.ggb
|
 5.4.2.2 B-Splines mit vielen Steuerpunkten
5.4.2.2 B-Splines mit vielen Steuerpunkten
|
Abschnitt
5.4.2.2
Seite 416
Aufl. 1
Seite 378

|
|
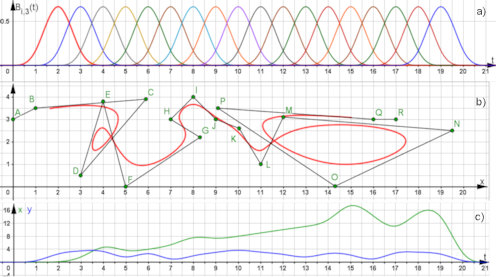
Abb. 5.22 Elemente eines langen
B-Splines für 18 Punkte (\(A\) bis \(R\)).
a) Basiskurven vom Grad 3,
die für 18 Punkte benötigt
werden. Sie sind jeweils in einem Intervall der Breite 4 definiert.
b) 18 Punkte, die das Gerüst für den B-Spline bilden, und der
B-Spline für \(3\le t\le 18\).
c) Die Graphen
\(P_x(t)=A_x B_{0,3}(t)+\dots+ R_x B_{17,3}(t)\) in Grün und \(P_y(t)\)
entsprechend in Blau.
 B-Splines3Grad.ggb
B-Splines3Grad.ggb
 B-Splines3Grad-PxPy-lang.ggb
B-Splines3Grad-PxPy-lang.ggb
|
 Zusatz Didaktische B-Splines,
Zusatz Didaktische B-Splines,
Polynome 4. Grades anstelle der rekursiv erzeugten B-Spline-Basen.
|
 Zusatz zu Zusatz zu
Abschnitt
5.4.2.2
Seite 416
Auflage 1:
Seite 378
|
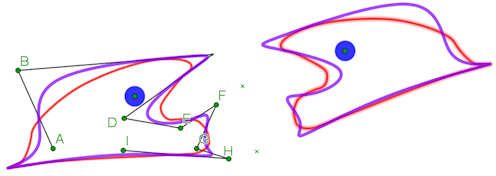 |
Didaktische B-Splines
Abb. 5.22.Z1
In den Vorträgen in Münster und Saarbrücken ist ein Vorschlag gemacht, wie Lernende eigenständig NURBS erfinden können, genauer Vortrag Münster Folien 7 bis 10.
Der Begriff NURBS wird dabei in allgemenem Sinne verwendet, auch für Basisfunktionen mit uniformen Knoten.
Die gleichmäßigen B-Spline können durch Polynome 4. Grades näherungsweise dargestellt werden. Leider ist dabei die Summe der Basisfunktionen auch nur angenähert 1.
Der Effekt ist links dargestellt: Die didaktischen Splines (rot) folgen nicht so gut dem Polygon der Stützpunkte wie der echte B-Spline (lila).
Dieser Mangel, Summe ist nicht 1, wird auch in der nächsten Zusatz-Betrachtung vertieft.
|
 Zusatz zu Zusatz zu
Abschnitt
5.4.2.2
Seite 417
Auflage 1:
Seite 378
|
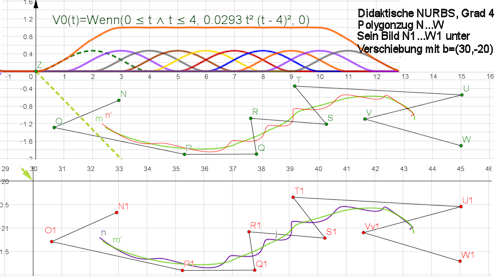
 Wirkung von "Nicht Summe 1" Wirkung von "Nicht Summe 1"
|
Warum muss die Summe der Basisfunktionen 1 sein?
Abb. 5.22.Z2
Bildet man die Steuerpunkte \(\{P_i\}=N,...,W\) affin mit einer Verschiebung um den Vektor \(\vec v=(30,-20)\) auf \(\{P'_i\}=N1,...,W1\) ab, so ist zu w ünschen, dass der Spline
aus den Bildpunkten \( \{P'_i\}\), unten violett dargestellt, auch wirklich mit dem affinen Bild(unten grün) des
Ur-Splines (der ist oben auch grün) übereinstimmt. Das ist HIER NICHT DER FALL, weil die
Basisfunktionen der "didaktischen Nurbs" NICHT die Summe 1 haben.
Der Spline der abgebildeten Punkte (unten violett) ist mit \(\vec u=(-30,+20) \) auch in die Umgebung des Ur-Splines,
oben als roter unpassender Spline, zurückgeschoben.

 Bezier+B-Splines22.nb, Mathematica Quelltext
Bezier+B-Splines22.nb, Mathematica Quelltext
 Dasselbe mit Mathematica-Player
Dasselbe mit Mathematica-Player
 Dies zum Lesen und Verstehen
Dies zum Lesen und Verstehen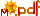
|
|
Escher-Metamophose
Eine Animation in Anlehnung an ein Bild von M. C. Escher: Ein Feld wird eine fliegende Gans
|

|
| |
Der niederländische Maler und Zeichner Mauritz C. Escher ist, gerade unter
Menschen, die Mathematik mögen, sehr bekannt. In einem
biografischen Film zu seinem 50. Todestag im Jahr 2022 haben die Autoren mehrere
seiner gezeichneten Tiere in animierten Szenen aus den Bildern krabbeln oder
fliegen lassen.
Davon angeregt haben wir die Metamorphose eines Feldes zu einer fliegenden Gans
aus dem berühmten Bild "Tag und Nacht" (1938) mit B-Splines umgesetzt.
In Abb. 5.24 kann man gut nachvollziehen, wie man mit B-Splines
auch praktisch arbeiten kann.
|
Abschnitt
5.4.2.2
Seite 417
Auflage 1:
Seite 378
|
 |



|
Abschnitt
5.4.2.2
Seite 4.17

|
|
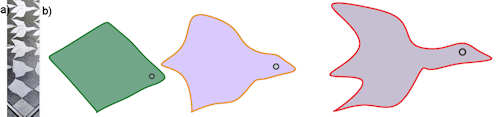
Abb. 5.23 Metamorphose eines Feldes in eine Gans
a) Schmaler Ausschnitt aus dem Bild "Tag und Nacht".
b Drei Stellungen aus der Animation, bei der sich das Feld stetig in
die fliegende Gans verwandelt. Dazu sind die Ecken des Polygonzuges durch
Strecken mit ebenso vielen Punkten auf dem Rand des linken Feldes verbunden
worden. Kopien der Polygonecken bekommen einen Parameter, durch den sie jeweils von
Anfang bis Ende ihrer Strecke "rutschen".
 Escher-Animation Escher-Animation
Die ggb-Datei beruht auf der Datei zu Abb. 5.22, nun aber mit 23 Punkten statt 18.
Sie finden auch die Herleitung und Möglichkeiten zu eigenen Kreationen.
Mit dem "Werkzeug Animation" können Sie in GeoGebra sehen, das auf diese Weise gespeichertes
animiertes gif-Bild ist oben zu sehen.
|
Abschnitt
5.4.2.2
Seite 4.17

|
|
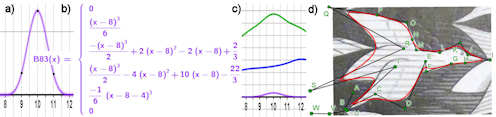
Abb. 524 Zusammenhang mit dem B-Spline
a) Gezeigt ist das Basiselement, das zu dem vordersten Schnabelpunkt
I gehört. I ist der 9. Punkt, Zählung ab 0, also Basiselement ab 8, das dann
die Koordinaten von I als Koeffizienten bekommt.
b) Gezeigt sind die 4 Funktionen, aus denen der Graph in a)
zusammensetzt ist.
c) Die grüne Kurve zeigt, dass der x-Wert von I bei $t=10$ am größten ist,
dort ist ja auch das Basiselement aus a) am höchsten. Die blaue Kurve zeigt
die y-Werte, für Punkt K hat sie ein relatives Maximum. Unten ist lilafarben das
Basiselement a) noch angezeigt.
d) Der Polygonzug ist der für Abb. 5.22 verwendete.
Hier aber hätte man, besonders
zwischen R und S, mit weiteren Punkten noch besser anpassen können.
|
 5.4.3 Gestaltung mit NURBS Teil 1
5.4.3 Gestaltung mit NURBS Teil 1
|
 5.4.3.1 Gebrochen rationale Bézier-Splines
5.4.3.1 Gebrochen rationale Bézier-Splines
|
| |
Anregung 5.2
Abschnitt
5.4.3
Seite sss

|
|
Anregung 5.2 (Rationale Parametrisierung des Einheitskreises EK) |
|
Eine bekannte rationale Parametrisierung des Einheitskreises ist:
\begin{eqnarray}
\text{Einheitskreis:}\qquad
\vec{K}(t) = \left(\frac{2t}{1+t^2},\frac{1-t^2}{1+t^2}\right),\
t\in (-\infty,\infty).
\end{eqnarray}
Versuchen Sie, diese herzuleiten, indem sie den Kreis
mit einer Geradenschar durch den Punkt \(N_1=(0,1)\) schneiden.
Klappt es auch mit \(N_2=(-1,0)\)?
Hinweis
Bei der in Abschnitt behandelten Trisektrix wird die
eben genannte Technik zur Beschaffung einer Parameterdarstellung ebenfalls angewendet.
 Kreis als NURBS und seine Nachbarn
Kreis als NURBS und seine Nachbarn
|
|
|
 5.4.3.2 Exakte Kurven und ihre Metamorphosen
5.4.3.2 Exakte Kurven und ihre Metamorphosen
|
| |
Anregung 5.3
Abschnitt
5.4.3.2
Seite 422

|
| |
Anregung 5.3 (Erkundung des NURBS für den Einheitskreises EK) |
|
Bauen Sie (z.B. mit GeoGebra)
Abb. 5.25 nach und lassen Sie \(C\) wandern. Sie können die GeoGebra-Datei
aus Abb. 5.25 verwenden.
Machen Sie sich klar, dass alle NURBS,
die nicht die Stellung \(y(C)=0.5\) realisieren, mathematisch bis ins Unendliche reichen.
Wenn Sie Enden sehen, sind das Artefakte.
Hinweis
Variieren Sie weitere Steuerpunkte. Sie könnten sich auch von diesem
Abschnitt 5.4.3.2 anregen lassen, Wege zu einem von Ihnen
definierten Ziel zu erfinden.
|
|
|
Abschnitt
5.4.3.2
Seite 423

|
 Kreis als NURBS und Nachbar-NURBS
Kreis als NURBS und Nachbar-NURBS
|
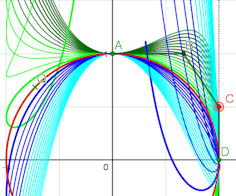
Abb. 5.25 Kreis als NURBS, Variation der Ordinate
von Steuerpunkt \(C\).
Punkt \(C\) ist in \(0.1\)-Schritten auf der Geraden \(x=1\) im Intervall
\([-0.5, 2]\) gewandert.
Die farbigen Kurven sind in GeoGebra mit dem Spurmodus entstanden.
Die große grüne Schlaufe links gehört zu \(y(C)=0.6\),
rechts die große blaue Schlaufe zu \(y(C)=0.4\).
Im Buch steht es leider falsch herum.
Für den exakten Kreis muss \(y(C)=0.5\) sein (rot).
Der Vorteil der Darstellung des Kreises als NURBS
besteht darin, dass man die Steuerpunkte nachträglich variieren kann.
|
 5.4.3.3 Trisektrix und ihre Verwandlung in einen Kreis
5.4.3.3 Trisektrix und ihre Verwandlung in einen Kreis
|
| | Die Trisektrix von MacLaurin hat die implizite implizite Gleichung
\((a+x)y^2=(3a-x)x^2\), ihr widmet sich Abschnitt 3.3.1 im Buch
Haftendorn: Kurven.
GeoGebra zeigt eine Schlaufe der Breite \(3a\) und einen Doppelpunkt im Ursprung. |
Abschnitt
5.4.3.3
Seite 423

|
|
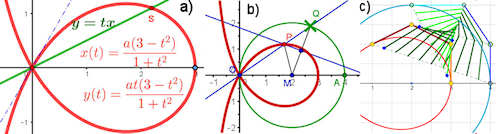
Abb. 5.26 Trisektrix Konstruktion und als NURBS
a) Trisektrix mit Parameterdarstellung.
\(\text{Trisektrix:}\quad x(t)=a \frac{3-t^2}{1+t^2}\;\mbox{ und }\;
y(t)=a\,t \frac{3-t^2}{1+t^2}\)
b) Konstruktion: Auf dem Kreis um \(M=(2a,0)\) läuft \(Q\).
Die Mittelsenkrechte auf \(\overline{MQ}\) schneidet die Gerade \(OQ\)in \($P\).
Die Ortslinie von \(\) bezüglich \(Q\) ist die Trisektrix.
c) In Anregung 5.4 soll das Ziel
für die Metamorphose der Trisektrix ihr grüner
Konstruktionskreis sein.
Die Gerüstpunkte sind gelb, der jeweils erste Balken des Gerüstes ist in hellerer
Farbe gezeichnet. Man erkennt so deutlich, dass das Gerüst umgewendet wird.
|
Abschnitt
5.4.3.3
Seite424

|
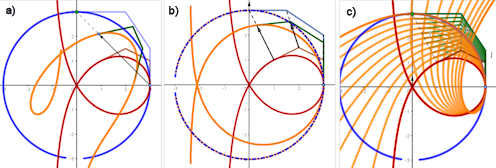
Durchlauf des blauen Kreises für t von 0 bis 1
Bild a) mathem. negativ, Uhrzeigersinn,
Bild b) mathem. positiv, entgegen dem Uhrzeigersinn,
Bild c) mathem. negativ, Uhrzeigersinn,
aber unpassend zugeordnet.
|
Abb. 5.27 Metamorphose mit NURBS: Trisektrix \(\rightarrow\) Kreis
a) Damit die Gerüste von Trisektrix und Kreis gemeinsam beginnen und
gleichsinnig durchlaufen werden, ist hier das Kreisgerüst gespiegelt. Dies
entspricht einem Tausch von \(x\) und \(y\) bei der Parametrisierung des Kreises.
Dann bläht sich die Trisektrix einfach auf, wandert aber zum gespiegelten Kreis.
b) Verwendet man das richtige ungespiegelte Gerüst des Kreises,
dann wird eine Umwendung der Trisektrix auf dem Weg zum Kreis erzwungen.
Der Kreis wird nämlich
vom Nordpol aus von links oben nach rechts durchlaufen, die Trisektrix
aber vom rechten Scheitelpunkt aus nach oben und dann links.
In c) sind mit dem Spurmodus neun NURBS dieser Metamorphose zu sehen, es
ist spannend zu beobachten, wie die asymptoten-nahen Punkte immer mehr in den Kreis gezogen
werden. Bei den Enden, die zu sehen sind, handelt es sich natürlich um Artefakte,
mathematisch reichen sie bis ins Unendliche, auch noch bei "Wanderparameter"
\(s=0.9\). Bei \(s=1\) hat der Kreis diese langen "Zipfel" plötzlich geschluckt. Die
Kreislücke unten könnte man nur durch größere Werte von \(t\) enger machen.
Dies zeigt, dass man den Kreis wohl nicht durch Herumprobieren gefunden hätte.
Aber das Gerüst der Trisektix ist ja exakt auf des Gerüst des Kreises abgebildet
worden.
Trisektrix-K-kreisZiel.ggb für 5.26 c)
d) zeigt das Gerüst des NURBS kurz vor der Umwendung, vgl.
Abb. 5.26 c).
|
| 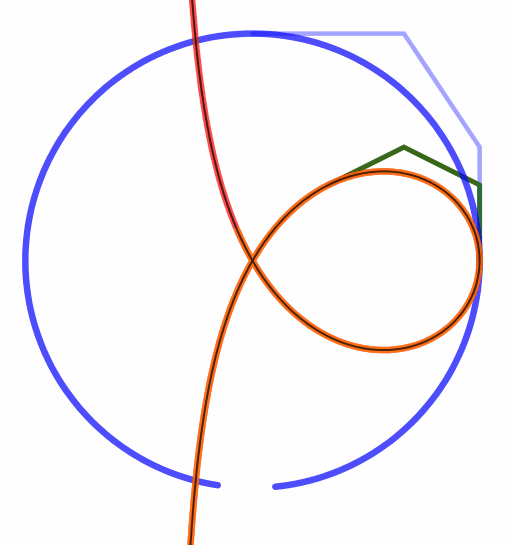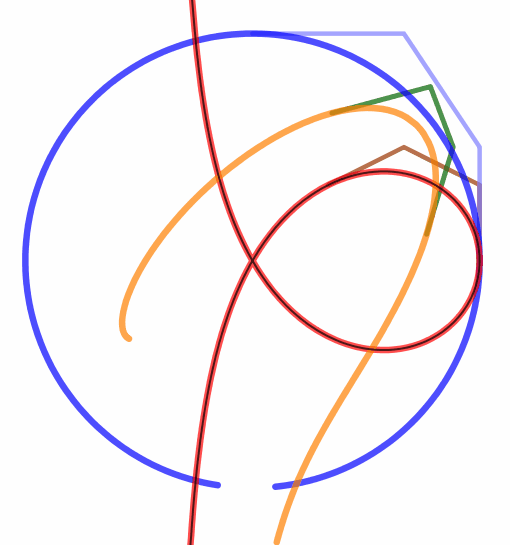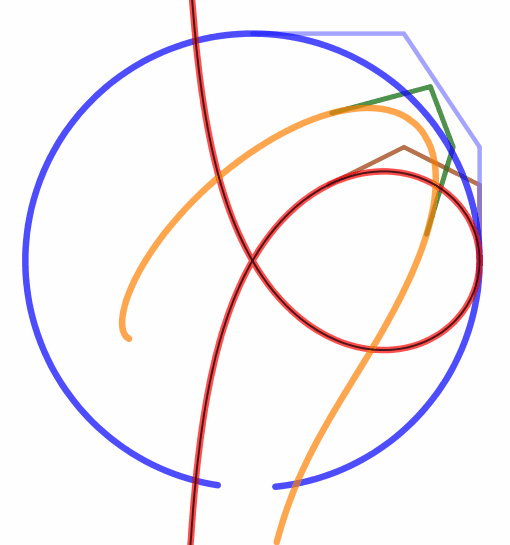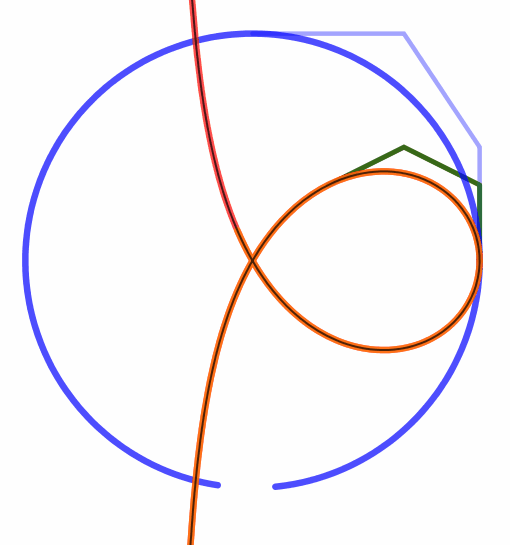 |
Metamorphose einer Trisektrix in einen Kreis mit Hilfe von rationalen Béziersplines
Zwei Parametrisierungen des Kreises werden hier verwirklicht und zwar genau nach dem eben beschriebenen Verfahren. Daher sind die beiden folgenden Mathematica-Realisierungen lediglich winzige Modifizierungen der oben genannten Datei.
Die beiden NURBS vom Kreis und die Trisektrix unterscheiden sich also nur durch die Stellung der Steuerpunkte. Darum verwirklicht die GeoGebra-Datei
eine gleichzeitige lineare Bewegung von einem Steuerpunkt zum entsprechenden anderen, wie in den Bildern angedeutet. Wir erhalten bei a) und b) eine
Metamorphose von der Trisektrix zum Kreis. Bei c) ist die Zuordnung wie bei b) aber der Kreis wie bei a). Damit gelingt die Verwandlung nicht.
a)  echte-Trisektrix-Kreis.ggb
echte-Trisektrix-Kreis.ggb \(A\rightarrow P_0,\;B\rightarrow P_1,\;C\rightarrow P_2,\;D\rightarrow P_3,\;\) die \(P_i\) gemäß dem Buch \(A\rightarrow P_0,\;B\rightarrow P_1,\;C\rightarrow P_2,\;D\rightarrow P_3,\;\) die \(P_i\) gemäß dem Buch
b)  echte-Trisektrix-anderer-Kreis.ggb
echte-Trisektrix-anderer-Kreis.ggb
c)  Trisektrix-Kr-Buch-o-Wenden.ggb
Trisektrix-Kr-Buch-o-Wenden.ggb
|
|
Trisektrix als rationaler Bézierspline
Die Grundidee ist es, eine Kurve dritten Grades mit rationalen Béziersplines darzustellen, denn wir wollen die Bernsteinpolyome
\(b_i\) verwenden, die ja Grad 3 haben. Wir haben uns für die Trisektrix entschieden, von der wir aus dem Kurvenbuch Seite 64 die
implizite Gleichung \((a+x)y^2=(3a-x)x^2\) kennen.
Nun benötigen wir eine rationale Parameterdarstellung.
Eine solche bekommt man, wenn man durch eine Singularität, also hier den Doppelpunkt im Ursprung, eine Gerade \(y=tx\) legt, sie mit der
Kurve zum Schnitt bringt und t als Parameter wählt. Sofort folgt \((a+x)t^2=(3a-x)\) und damit
\(x(t)=\frac{a(3-t^2)}{1+t^2}\). Aus der Geradengleichung folgt dann
\(y(t)=\frac{at(3-t^2)}{1+t^2}\).
Die rationale Basis, die wir verwenden wollen, ist nach Seite 379 unten
\(R_i=\frac{w_i b_i}{\Sigma_{j=0}^3{w_j b_j}}\), für \(i=0\dots3\).
In der Linearkombination der \(R_i\) mit den Steuerpunktkoordinaten als Koeffizienten gilt der gemeinsame Nenner
\(\Sigma_{j=0}^3{w_j b_j}=1+t^2\) ohne Einfluss der Steuerpunkte. Durch Koeffizientenvergleich der Potenzen von \(t\) bestimmen wir
\(w_0=1,\;w_1=1,\;w_2=\frac{4}{3},\;w_3=2\). Beim Kreis (s.o.) ist es (zufällig) derselbe Nenner.
Mit diesen Gewichten im Zähler ergibt sich, wie im Buch Seite 380, die rationale Basis:
\(R_0(t)=\frac{(1-t)^3}{t^2+1},\;R_1(t)=\frac{3 (1-t)^2 t}{t^2+1},\;R_2(t)=\frac{4 (1-t) t^2}{t^2+1},\;R_3(t)=\frac{2 t^3}{t^2+1}\).
Die Steuerpunkte müssen nun so gewählt werden, dass der Gesamtzähler der Linearkomination
\(A\,R_0+B\,R_1+C\,R_2+D\,R_3\) für \(x(t)\) und \(y(t)\) der Zähler der Parameterdarstellung der Trisektrix ist:
\( a(3-t^2)=A_x(1-t)^3+B_x 3 (1-t)^2 t+C_x4 (1-t) t^2+D_x 2 t^3\)
\( at(3-t^2)=A_y(1-t)^3+B_y 3 (1-t)^2 t+C_y4 (1-t) t^2+D_y 2 t^3\)
Durch Koeffizientenvergleich erhält man aus einem Gleichungssystem
\(A=(3 a,0),\,B=(3 a,a),\,C=\left(2 a,\frac{3 a}{2}\right),\,D=(a,a)\) als Steuerpunkte einer Trisektix mit dem Doppelpunkt im Ursprung und der Schlaufenbreite 3\(a\).
 Trisektrix-rat-Bezierspline.cdf,im Mathematica Player Trisektrix-rat-Bezierspline.cdf,im Mathematica Player , Info zum Player , Info zum Player
 Trisektrix-rat-Bezierspline.nb, Mathematica Quelltext Trisektrix-rat-Bezierspline.nb, Mathematica Quelltext
 Dies zum Lesen und Verstehen Dies zum Lesen und Verstehen
|
| |
Anregung 5.4
Abschnitt
5.4.3.3
Seite 423

|
| |
Anregung 5.4 (Metamorphose der Trisektrix in ihren Konstruktionskreis) |
|
Die Parameterdarstellung (\(x(t),y(t))\) als NURBS von Gleichung 5.7 (Seite 422 des Buches) für den Einheitskreis
kann leicht auf andere Kreise übertragen werden. Einen Kreis
\((\bar x(t),\bar y(t))\) mit Radius \(r\) und
dem Mittelpunkt \((a,b)\) parametrisiert man nun durch
\(\bar{x}(t):=r\, x(t)+a\) und \(\bar{y}(t):=r\, y(t)+b\). Für das Gerüst nimmt
man einfach die \(r\)-fache Größe und "heftet" es an einen Kreispunkt an.
Aufgabe: Lassen Sie die Trisektrix zu ihrem Konstruktionskreis wandern.
Es kann Ihnen jetzt bewusst werden, dass fast die ganze Arbeit schon erledigt ist.
Ziel ist nun der Kreis in Abb. 5.26 b) und c), sein Radius ist
\(r=2\) und sein Mittelpunkt \((2,0)\). Das oben
berechnete Gerüst des Kreisesübertragen Sie geometrisch auf den
verschobenen und vergrößerten Kreis. Darum brauchen Sie die
Kreisgleichung gar nicht.
Definieren Sie einen Schieberegler
\(s \in [0,1]\) und konstruieren Sie mit dem hier folgenden Hinweis die Punkte
\(A',\;B',\;C',\;D'\) auf den Wegen zum Kreisgerüst. Diese setzen Sie als Namen
mit \(x(A'),\;\dots \) bzw. \(y(A'),\;\dots \) in
Gleichung auf Seite 421 ein. Fertig ist Ihre erste NURBS-Wanderung.
Hinweis
Wenn ein Punkt \(A\) als \(A'\) gesteuert von einem Parameter \(s\) zum Punkt \(E\)
wandern soll, definieren Sie in GeoGebra
\(ae=vektor(A,E)\; \;tt ae=Vektor(A,E') \). Es ist dann \(tt A'=A+s \;ae\)
der gesuchte wandernde Punkt. Anmerkung: In GeoGebra kann man Punkte und Vektoren
addieren, man braucht dabei keine "Ortsvektoren" zu definieren.
|
|
|
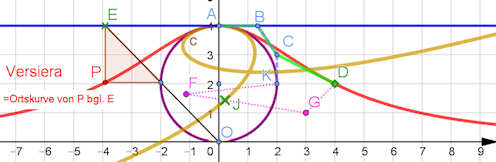
 5.4.3.4 Versiera Konstruktion und ihre Verwandlung in einen Kreis
5.4.3.4 Versiera Konstruktion und ihre Verwandlung in einen Kreis
|
|
Im Buch Haftendorn: Kurven finden Sie Interessantes zur Versiera von Maria
Agnesi (1718-1799). Die einfache Konstruktion ist in
Abb. 5.28 im gezeigt: Auf der
Nordpol-Tangente des Kreises um \((0,a)\) mit Radius \(a\) wandert ein Punkt \(E\).
Die Gerade \(E\) schneidet den Kreis in \(E'\). Dann bekommt \(P\) die Abszisse von \(E\) und die Ordinate
von \(E'\). Die Ortskurve von \(P\) ist die Versiera.
|
Abschnitt
5.4.3.4
Seite 425

|
|
Abb. 5.28 NURBS der Versiera der Maria Agnesi.
Die Konstruktion wird oben erklärt, die implizite
Gleichung und ihre Parametrisierung wird hergeleitet.
Ihr Gerüst wird berechnet und mit frei erfundenem Weg wird die
Metamorphose zu ihrem Konstruktionskreis realisiert.
versiera-kreis
versiera-NURBS
Versiera-rat-Bezierspline.nb
|
 5.4.3.5 NURBS für die Bernoulli'sche Lemniskate, eine Kurve 4. Grades
5.4.3.5 NURBS für die Bernoulli'sche Lemniskate, eine Kurve 4. Grades
|
| Seite 426 |
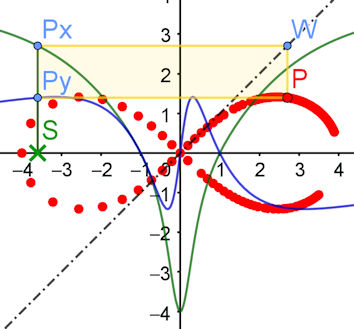
| Bernoulli'sche Lemniskate
\[
\text{Bernoulli'sche Lemniskate:}\qquad (x^2+y^2)^2=a^2(x^2-y^2)
\]
Im Buch Haftendorn Kurvenbuch finden wir in Gleichung 4.29 eine rationale Parametrisierung für die
\[
\text{Bernoulli'sche Lemniskate:} \qquad x(t)=a\frac{1-t^4}{1+6t^2+t^4},
\quad y(t)=a\frac{2 t (1-t^2)}{1+6t^2+t^4}.
\]
Visualisierung der Parameterdarstellung der Lemniskate
In der GeoGebra-Datei sind links in Grün die Funktionen \(x(t)\) und in Blau \(y(t)\) dargestellt. Punkt \(S\) repräsentiert den Parameter \(t\), hier \(s\) genannt. Von \(P_x=(t,x(t))\) wird die Ordinate an der Geraden \(y=x\)
gespiegelt, um dann als Abszisse von \(P\) verwendet zu werden. \(P_y=(t,y(t))\) überträgt man waagerecht bis zur Geraden \(y=x(t)\). So entsteht \(P=(x(t),y(t))\), die Ortslinie von \(P\) ist die
Bernoullische Lemniskate
 Lemniskate Lemniskate
|
Der NURBS für Kurven 4. Grades mit dem Nenner \(1+6t^2+t^4\) ist:
\(
\left(\begin{matrix} x(t)\\y(t)\end{matrix}\right)=\frac{1}{1+6t^2+t^4}\cdot\\
\Big( A\cdot (1-t)^4 +B\cdot 4(1-t)^3 t + C\cdot 12(1-t)^2 t^2+D\cdot 16(1-t) t^3+E\cdot 8 t^4 \Big)
\)
Die Lemniskate erhalten wir nur dann, wenn wir ihr Gerüst berechnen. Dafür muss die
große Klammer mit den Abszissen der Punkte \((1-t^4)\) und mit den Ordinaten
\(2t -2 t^3\) ergeben. Ein passendes Gleichungssystem haben wir oben mehrfach durch
Koeffizientenvergleich gelöst. Tun wir das hier ebenso, so ergibt sich das
folgende Ger üst der
\(\text{Lemniskate: }\quad A=(4,0),\;B=(4,2),\;C=(2,2),\;D=(1,1),\;E=(0,0)\).
|
Abschnitt
5.4.3.5
Seite 472

|
|
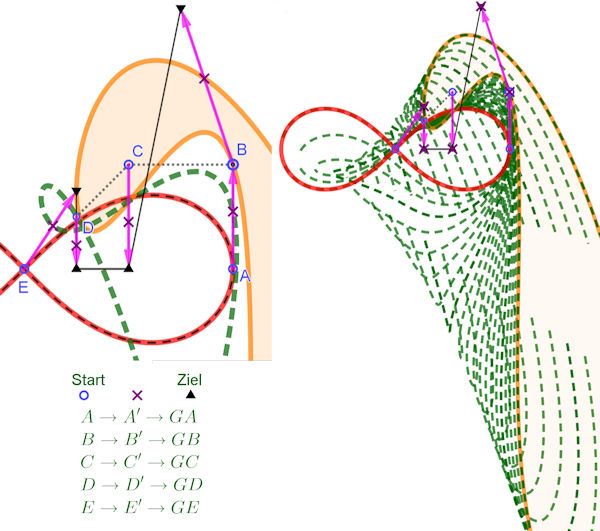
Abb. 5.28 Lemniskate und Giraffe mit NURBS
Die Giraffe saugt die Lemniskate an sich und hat sie dann als Mantel an.
Die Lemniskate für \(a=4\) hat das Gerüst
\(A=(4,0),\;B=(4,2),\;C=(2,2),\;D=(1,1), \;E=(0,0)\),
zu sehen als blaue offene Kreise,
wobei \(A\) der rechte Scheitelpunkt ist und \(E\) der Doppelpunkt.
Diese Punkte sind gedoppelt worden (violette Kreuze) und deren
Linearkombination ist der NURBS.
Diese Kreuze sind ganz frei
umhergezogen worden, bis die entstandene Form gut aussah. Dann konnten die pinkfarbenen
Vektoren definiert werden und ihr \(s\)-Faches \(A',\;B',\;C',\;D',\;E'\) als Wanderpunkte einen weiteren
NURBS definieren.
Der Parameter \(s\) lief für die grünen Kurven von \(s=0\) bis \(s=1 \).
Der Mantel ist für \(s=1\) zu haben.
Wie man den NURBS wandern lässt, ist oben erklärt.
Sie können die "Wanderwege" (in Pink) deutlich sehen.
Lemniskate+Giraffe.ggb
|
|
 5.4.4 NURBS, Teil 2, mit nicht uniformen Basen
5.4.4 NURBS, Teil 2, mit nicht uniformen Basen
|
| | Gebrochen rationale B-Spline-Basen:
Ebenso wie in NURBS Teil 1 für rationale Basen mit Bézier-Splines führen wir auch
hier rationale Basen mit den allgemeineren nicht-uniformen B-Splines ein:
\[
R_{i,p}(t)=\frac{w_i\cdot B_{i,p}(t)}{\sum_{j=0}^n\cdot w_j B_{j,p}(t)}
\text { mit } i \in \{0,\dots, 4\}.
\] |
Abschnitt
5.4.4
Seite 428
Auflage 1:
5.4.3.1
Seite 379

|

|
Abb. 5.30 Nicht-uniforme NURBS.
a) Basiskurven vom Grad 3, je fünf benachbarte Knoten
aus der Liste \(T\) gehören zu einer Basis-Funktion 3. Grades für B-Splines.
b) Bei einem rotgestrichelten
Viertelkreis mit Gerüst, siehe Abb. 5.25, wird hier unter Beibehaltung des Gerüstes
das Gewicht eines Punktes variiert. Im Text wird die ganz unterschiedliche Wirkung betrachtet.
c) Sieben Basiskurven nicht-uniformer, rationaler B-Splines zweiten Grades
d) Ein geschlossener NURBS daraus daraus mit 7 Steuerpunkten und
nicht uniformen, rationalen B-Splines zweiten Grades, der aus vier
Ellipsenstücken besteht. Die Funktionen sind in der Mathematica-Datie und in GeoGebra
einsehbar und das Gerüst ist in GeoGebra frei ziehbar.
|
| a) und b)  NURBS1 zum Viertelkreis in vielfätiger Datei, Splines-und-NURBS.nb Mathematica Quelltext NURBS1 zum Viertelkreis in vielfätiger Datei, Splines-und-NURBS.nb Mathematica Quelltext
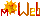 Dies zum Lesen und Verstehen Dies zum Lesen und Verstehen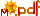
c) und d)  NURBS2.ggb
NURBS2.ggb
|
 5.4.4.1 Beispiel eines geschlossenen NURBS 5.4.4.1 Beispiel eines geschlossenen NURBS
|
|
Das Schließen eines NURBS wie in Abb. 5.30 d) erfordert die
Wiederholung des ersten Steuerpunktes als letzten Punkt, hier ist \(P_6=P_0\).
Die nicht-uniforme rationale Basis ist auf der Grundlage von
B-Splinepolynomen 2. Grades erstellt worden und in Abb. 5.30 c) zu
sehen. Zusätzlich zu dem bisher Gesagten wird ein
weiterer Trick benutzt, nämlich
die Wiederholung von Einträgen in der Knotenliste.
In der Rekursion entstehen
dadurch manchmal Intervalle der Breite 0,
die - und das funktioniert wirklich -
einfach nicht berücksichtigt werden. Daraus entstehen zwei Effekte,
nämlich eine engere
Anlehnung der Kurve an das Gerüstpolygon, in Abb. 5.30 d)
deutlich zu sehen, und eine Verringerung der Differenzierbarkeit an
zugehörigen Steuerungspunkten. Die Knotenliste lautet hier
\(T=\{0,0,0,\frac{1}{4},\frac{1}{2},\frac{1}{2},\frac{3}{4},1,1,1\}\).
Die Verdreifachung der 0 und der 1 führt dazu, dass \(P_0\) und \(P_6\) genau
getroffen werden. Die mittlere Basisfunktion in Abb.5.30 c) z.B.
ist wegen der doppelten \(\frac{1}{2}\) nicht mehr differenzierbar, erkennbar
an der Spitze in Bildmitte. Die resultierende Kurve ist aber trotzdem wegen
geschickt gewählter Gewichte zweimal stetig differenzierbar.
Die sieben Steuerpunkte und die zugehörigen Basisfunktionen in Abb. 5.30
haben in c) und d) dieselbe Farbe. Sie lassen sich auf der obigen GeoGebra-Datei
zum Buch ganz frei ziehen. Der abgebildete NURBS besteht
aus vier Ellipsenbögen, die von einem Berührpunkt zum nächsten reichen.
In GeoGebra kann man sich das durch das Werkzeug
"Kegelschnitt aus 5 Punkten" anzeigen lassen, hier z.B. \( (A,B,C,D,P_3)\).
Wenn das Gerüst ein Parallelogramm ist, erreicht man eine exakte vollständige
Ellipse, bei einem Gerüst-Quadrat erhält man einen perfekten Kreis.
|
 5.4.4.2 Doppelte Knoten in der Knotenliste
5.4.4.2 Doppelte Knoten in der Knotenliste
|
Abschnitt
5.4.4.2
Seite 428
Auflage 1:
5.4.3.2
Seite 430

|
a)
a)Zusatz
b)
 NurbsKnotendoppelt.ggb
NurbsKnotendoppelt.ggb
|
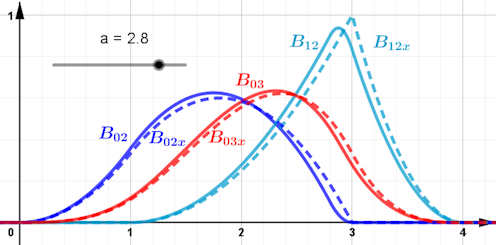
Abb. 5.31 Doppelte Knoten in der Knotenliste
a) Zu der Knotenliste \( (0,1,a,3,4)\) werden hier die Basisfunktionen
\( B_{02},\, B_{12} \) und \( B_{03} \) mit \( a=2.8 \) gezeigt, und dazu die Basisfunktionen
\( \bar B_{02},\ \bar B_{12} \) und \( \bar B_{03} \) zur Knotenliste
\( (0,1,3,3,4) \), letztere gestrichelt. Diese wurden unter Weglassen des
Intervalls \( [3,3] \) mit Länge 0 berechnet.
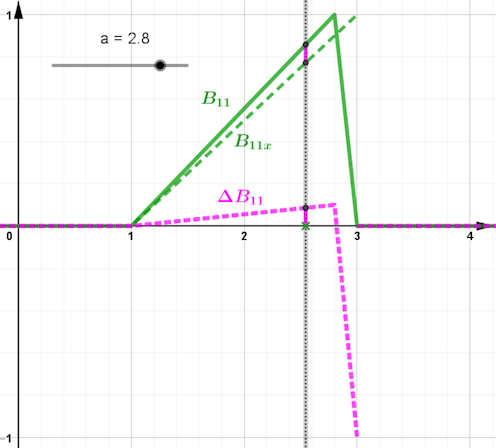
b) Hier werden die Basisfunktionen \( B_{11} \) und \( \bar B_{11} \) gezeigt,
dazu deren Differenz \( \Delta B_{11} \).
Ersichtlich geht diese für \( a\to3 \) im Intervall \([1,a]\) gegen null.
Das Intervall \( [a,3]\) - in dem wir \( \Delta B_{11} \) nicht ganz vollständig
gezeichnet haben - schrumpft auf die Breite null. Daher liegt punktweise Konvergenz für
\(B_{11} \to \bar B_{11}\) vor.
Doppelte Knoten in NURBS, Erläuterungen
Im Buch steht auf Seite 380 zu den geschlossenen NURBS, dass als nötiger Trick Elemente
in der Knotenliste verdoppelt werden, und dass man die dadurch in der Rekursion entstehenden
Intervalle der Länge 0 einfach weglassen soll. Als Erklärung wird nur geboten,
dass das "tatsächlich funktioniert".
Wir wollen hier aber begründen, dass dieses Weglassen der richtige Weg ist.
 NurbsKnotendoppelt.ggb
NurbsKnotendoppelt.ggb
In dieser GeoGebra-Datei werden zur Knotenliste {0,1,2,3,4} die Basispolynome
\(B_{00},\ B_{10},\ B_{20},\ B_{30},\ B_{01},\ B_{11},\ B_{21},\ B_{02},\ B_{12}\) und \(B_{03}\) eines NURBS berechnet.
Sie können in der GeoGebra-Datei links im Algebrafenster die Funktionen auswählen, die sie sehen wollen.
Dort können Sie auch rekursiven Definitionen verfolgen und die Funktionsterme sowie die Graphen ansehen.
Links sind durchgezogen\( B_{02},\ B_{03}\) und \(B_{12}\) zu sehen, die gestrichelten Graphen werden im Folgenden erklärt.
Der Knoten 2 ist über einen Schieberegler \(a\) veränderbar, er kann im Bereich 2 bis 3 verschoben werden. Das heißt, dass Sie den Knoten 3 verdoppeln können. Dabei können Sie sich anschauen, wie sich der Verlauf der Funktionen ändert. Bei \(B_{11}\) werden Sie den Bruch \(\frac{3-x}{3-a}\) als Teilterm entdecken. Dieser ist für \(a=3\), also den verdoppelten Knoten, nicht definiert. Ziehen Sie \(a\) auf 3, wird \(B_{11}\) nicht mehr angezeigt, und alle vom Intervall [a,3] abhängigen Funktionen auch nicht. Deshalb gibt es die Funktionsversionen \(B_{10x},\ B_{01x},\ B_{11x},\ B_{21x},\ B_{02x},\ B_{03x}\) und \(B_{12x}\) (alle gestrichelt), die undefinierte Teilterme weglassen und \(a=3\) setzen. \(B_{20}\) wird nicht mehr gebraucht. Im ersten Bild links oben sind \(B_{02},\ B_{03},\ B_{12},\ B_{02x},\ B_{03x}\) und \(B_{12x}\) gezeigt für \(a=2.8\), im Bild links Mitte nur \(B_{02x},\ B_{03x}\) und \(B_{12x}\) für \(a=3\). Sie können sehen, wie sich die durchgezogenen Funktionen an die gestrichelten annähern, wenn \(a\to3\) geht.
Wir wollen zum Verstehen durch Anschauen aber auch noch einen rechnerischen Beweis liefern, und zwar für \(B_{11}\), welche Funktion ja sozusagen der "Anfang allen Übels" ist. Dazu können Sie sich auch die Funktion \(\Delta B_{11} = B_{11} - B_{11x}\) anzeigen lassen, wie es im unteren Bild für \(a=2.8\) geschehen ist. Es ist
\[
\Delta B_{11} = \left(\frac{x-1}{a-1} - \frac{x-1}{3-1}\right)B_{10} + \left(\frac{3-x}{3-a} - \frac{x-1}{3-1}\right)B_{20}=
\]
\[
= (3-a)\frac{x-1}{(a-1)(3-1)}B_{10} + \text{ irgendwas }\cdot B_{20}.
\]
Der linke Summand geht gegen 0, wenn \(a\to3\) geht, der rechte ist nur auf dem Intervall [a,3] von null verschieden. Daraus folgt, dass \(\Delta B_{11}\to0\) punktweise geht für \(a\to3\), oder anders gesagt \(B_{11}\stackrel{a\to3}\longrightarrow B_{11x}\) punktweise.
Eine analoge Rechnung gelingt in allen anderen Fällen ebenso. Schauen Sie sich auch an, wie die Grenzfunktionen für \(a=3\) im doppelten Knoten einmal weniger differenzierbar sind als ohne doppelten Knoten (0-mal differenzierbar heißt dabei einfach "stetig") und überlegen Sie, dass das daran liegt, dass die Gewichtsfunktionen am Intervallrand am doppelten Knoten keine Nullstelle mehr haben: der dazu nötige Term wird gerade weggelassen!
|
 5.4.4.3 NURBS-3D in der Praxis
5.4.4.3 NURBS-3D in der Praxis
|
| | Wir haben hier nur Grundlegendes mit wenigen Steuerpunkten gezeigt. Aber auch
dafür brauchte man schon ein kräftiges CAS,
vor allem um die Rekursionen und die mehrfach indizierten Terme zu handhaben.
Im letztgenannten Beispiel haben wir die Ergebnisse aus
Mathematica nach GeoGebra übertragen. So aber konnten Sie die Grundgedanken
verstehen.
Wenn Sie Genaueres wissen wollen, suchen Sie im Internet nach neuen
Veröffentlichungen, denn das Thema befindet sich in schneller
Entwicklung. "The NURBS Book" von Piegl ist ein älteres, aber
ausführliches Grundlagenbuch dazu.
Wir zeigen Ihnen dieses Bild, weil in Animationsfilmen ja auch dreidimensionale
Objekte dargestellt werden müssen.
|
Abschnitt
5.4.4.3
Seite 431
Auflage 1:
5.4.3.4
Seite 381

|
|
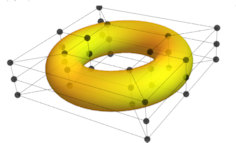
Abb. 5.32 Torus als NURBS. In der Praxis gibt es
ausgereifte Software für NURBS, die dem Anwender die Mühen abnimmt. Das gilt
insbesondere für den Einsatz im 3D-Bereich. Im Gegensatz zu einfacheren
Konzepten für Splines können NURBS sowohl Freiformen als auch Standardformen
wie Zylinder, Kegel, Ringe, Kugel u.s.w. gestalten.
 NURBS-Torus.nb, Mathematica Quelltext NURBS-Torus.nb, Mathematica Quelltext
 Dies zum Lesen und Verstehen Dies zum Lesen und Verstehen
|
 5.5 Numerische Integration
5.5 Numerische Integration
|
 5.5.1 Kepler'sche-Regel
5.5.1 Kepler'sche-Regel
|
Abschnitt
5.5.1.1
Seite 433
Auflage 1:
Seite 383

|
|
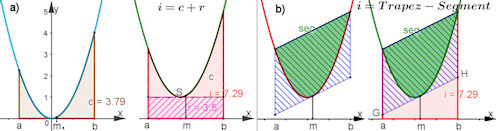
Abb. 5.33 Beweise der Kepler'schen Regel:
a) beweist mit der linken Parabel eine
Sondersituation, die dann rechts daneben verwendet wird.
b)
zeigt den historischen, geometrischen Weg von Archimedes und Kepler.
Ein Parabelsegment (grün) nimmt immer \(\frac{2}{3}\) des
umbeschriebenen (blau gestreiften) Parallelogramms ein.
 kepler-beweise.ggb
kepler-beweise.ggb
|
Abschnitt
5.5.1.1
Seite 434
Auflage 1:
Seite 384

|

|
Abb. 5.34 Allgemeine Aussage über Parabelsegmente,
bewiesen mit Integralrechnung und Scherung.
Näheres dazu im Text.
 parabelsegment.ggb
parabelsegment.ggb
|
Abschnitt
5.5.1.2
Seite 435
Auflage 1:
Seite 385

|
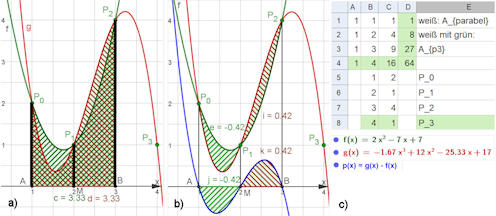
|
Abb. 5.35 Kepler'sche Regel für eine Parabel und
ein Polynom $p_3$.
a) Die beiden Integralflächen haben zwar nicht
dieselbe Form, aber dieselbe Fläche.
b) Der Grund ist, dass das Integral über ihre Differenzfunktion null
ist.
c) Kleines Lehrstück zur Bestimmung der Interpolationspolynome mit in
GeoGebra definierten Matrizen (siehe Text und den folgenden Zusatz).
 kepler1.ggb
kepler1.ggb
 kepler2.ggb
kepler2.ggb
|
 5.5.2 Simpson-Regel
5.5.2 Simpson-Regel
|
Abschnitt
5.5.2
Seite 436
Auflage 1:
Seite 386

|
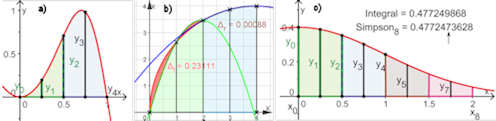
|
Abb. 5.36 Simpson'sche Regel an Beispielen.
a) zeigt die Simpson-Regel mit 4 Streifen der Breite \(h=0.25\) für die
Funktion \(\sin(\pi x^2)\).
In b) wird die Viertelkreisfläche mit ebenfalls 4 Streifen der Breite
1 angenähert, aber mit bescheidenem Erfolg.
Genaueres im folgenden Zusatz
c) zeigt eine Näherung für die wichtige
Gauß'sche Glockenkurve mit 8 Streifen, der Fehler liegt unter 3
Millionstel.
Weiteres zu den gezeigten Näherungen steht im
Abschnitt 5.5.2.2 nach der
Simpson-Formel in Satz 5.5 und der
Fehlerbetrachtung 5.5.2.1.
|
 Zusatz Zusatz
zum
Teil b) |
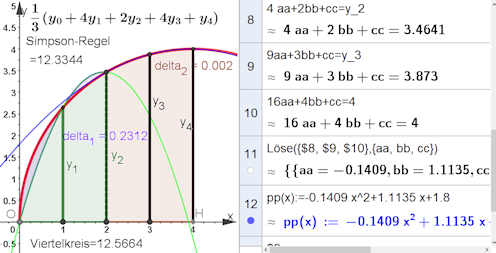 |
 simpson-a.ggb Sinus
simpson-a.ggb Sinus
 simpson-b.ggb Viertelkreis
simpson-b.ggb Viertelkreis
 simpson-c.ggb Glockenkurve
simpson-c.ggb Glockenkurve
Die Breite zweier benachbarter Balken sollte so gewählt werden, dass man das zugehörige Kurvenstück annähernd als Parabel (oder Poymom 3. Grades) auffassen kann.
Bei dem Viertelkreis in b) sind die zugehörigen Parabeln eingezeichnet. Es ist daher klar, dass der linke Doppelbalken einen deutlichen Fehler erzeugt.
In der rechten Bildhälfte ist GeoGebra-CAS zu sehen.
Es werden damit die Parabeln berechnet, die die Grundlage der Rechnung sind.
Achten Sie in  simpson-b.ggb Viertelkreis
simpson-b.ggb Viertelkreis auf das CAS-Fenster. Man macht es bei Ansicht mit Strg+Umschalt+K (zweimal diesen Hotkey klicken) auf. auf das CAS-Fenster. Man macht es bei Ansicht mit Strg+Umschalt+K (zweimal diesen Hotkey klicken) auf.
|
 5.5.3 Weitere Verfahren der numerischen Integration
5.5.3 Weitere Verfahren der numerischen Integration
|
 5.5.3.1 einfache Methoden
5.5.3.1 einfache Methoden
|
Abschnitt
5.5.3.1
Seite 440
Auflage 1:
Seite 392

|
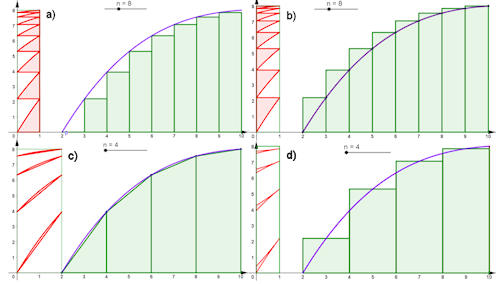
|
Abb. 5.37 Fehler einfacher
Quadraturformeln. Es ist in jedem Bild die approximierte
Integralfläche im Vergleich mit der wirklichen Integralfläche zu sehen.
Die Fehlerflächen sind nach links zusammengeschoben und liegen auf
einem Streifen der Breite \(h\) bzw. bei d) \(\frac{h}{2}\). Einzelheiten stehen
im Text. In der GeoGebra-Datei können Sie mit \(n\) die
Anzahl der Streifen verändern und das Fehlerverhalten verstehen.
 FehlerObersumme.ggb
FehlerObersumme.ggb
 FehlerUntersumme.ggb
FehlerUntersumme.ggb
 FehlerTrapezsumme.ggb
FehlerTrapezsumme.ggb
 FehlerMittenregel.ggb
FehlerMittenregel.ggb
|
 5.5.3.2 Mittenregel
5.5.3.2 Mittenregel
|
Abschnitt
5.5.3.2
Seite 441
Auflage 1:
Seite 392

|
|
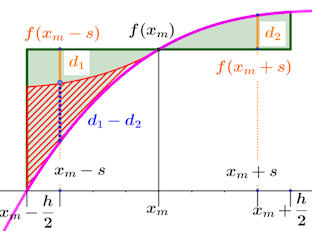
Abb. 5.38 Abschätzung des
Fehlers bei der Mittenregel.
In der linken Hälfte überschätzt die Mittenregel das Integral um die
grüne Fläche, in der rechten unterschätzt sie ebenfalls um die grüne
Fläche. Durch Punktspiegelung dieser an der Mitte kann man links die
Differenzfläche (rot schraffiert) als Gesamtfehler erkennen.
Sie hat jeweils Ordinatenstücke der
Länge \(d_1-d_2\), (gelb).
Diese roten Differenzflächen sind in Abb. 5.37 d)
bei der Mittenregel abgebildet.
 RechnungMittenregel.ggb
RechnungMittenregel.ggb
|
 5.5.3.3 Newton-Cotes-Formel, Drei-Achtel-Regel
5.5.3.3 Newton-Cotes-Formel, Drei-Achtel-Regel
|
Abschnitt
5.5.3.3
Seite 442 |
Newton-Cotes-Formel, Drei-Achtel-Regel
\[
\int_a^b f(x)\,d x \approx \frac{3h}{8}\bigl(f(a) + 3f(a+h) +
3f(a+2h) + f(b)\bigr).
\]
Eine Funkton \(f\) ist im Intervall näherungsweie zu integrieren. Erleichterungen für
solche Aufgaben sind heute weniger wichtig, da die Computer dergleichen schnell erledigen können.
Dennoch ist es lehrreich, mit wie wenigen Stützstellen man schon zu recht guten oder sogar exakten Antworten kommt.
Letzteres gilt vor allem für Polynome, die Drei-Achtel-Regel integriert Polynome bis zum 3. Grad exakt.
|
Abschnitt
5.5.3.3
Seite 442
Auflage 1:
Seite 393

|
|
Drei-Achtel-Regel
Das Intervall \( [a,b]\) wird in 8 gleiche Teile geteilt, diese werden zu 1 Achtel,
3 Achtel, 3 Achtel und nochmal 1 Achtel gruppiert. Es entstehen vier Rechtecke, die
ihre Ordinaten von \(f\) am Intervallrand und an den zwei inneren Drittelstellen \(C\)
und \(D\) bekommen. So ist es im Bild gezeigt. Das Intervall ist also in drei Streifen
der Breite \(h=\frac{b-a}{3}\) geteilt. Rechtecke, die unter der x-Achse liegen, müssen
negativ gerechnet werden. Hier sind sie daher durch Integrale bestimmt worden. Durch
die vier Stützpunkte \({E,\,C,\,D, F}\) ist hier mit dem GeoGebra-Befehl: Polynom[Punkteliste]
das Interpolationspolynom gelegt.
Man kann \(A \text{ und } B \) auf der x-Achse und die anderen grünen
Punkte auf ihren roten Stangen beliebig ziehen.
 Newton-C.-3AchtelRegelExakt.ggb Newton-C.-3AchtelRegelExakt.ggb  
 Newton-C.-3AchtelRegelExakt2.ggb Newton-C.-3AchtelRegelExakt2.ggb 
|
Abschnitt
5.5.3.3
Seite 442

|
|
Drei-Achtel-Regel allgemein: nur eine Näherung
Hier ist unten rechts (als blaue Raute) noch ein fünfter Punkt für die
Liste, die
das Interpolationspolynom erzeugt, eingefügt. Ersichtlich ist damit ein
Polynom 4. Grades entstanden und die Drei-Achtel-Regel gibt nicht mehr das Integral an.
 Newton-C.-3AchtelRegel-allg.ggb Newton-C.-3AchtelRegel-allg.ggb 
Anmerkung: Es kann nicht passieren, dass die roten Stangen der Stüzpunkte
auf die Ecken der inneren Rechtecke fallen, da 8 und 3 teilerfremd sind.
Anderenfalls könnte es zu Uneindeutigkeiten kommen.
|
 5.5.3.4 Gauß-Quadratur
5.5.3.4 Gauß-Quadratur
|
Abschnitt
5.5.3.4
Seite 444
Auflage 1:
Seite 395

|
|
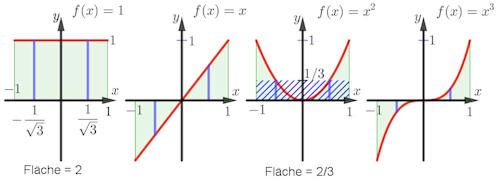
Abb. 5.39 Die erste
Gauß'sche Quadraturformel integriert Polynome bis zum Grad 3
exakt: von links nach rechts sind die Funktionen \(f(x)=1,\ x,\ x^2,\ x^3\)
gezeigt. In blau sieht man jedes Mal die Ordinaten an den Stützstellen
\(\pm\frac{1}{\sqrt3}\), diese Werte sind aber nur ganz links eingetragen.
Außerdem ist für \(x^2\) das (blau schraffierte) Rechteck gezeigt,
das die Fläche nach der Gauß'schen Quadraturformel darstellt.
 GaussQuadratur.ggb
GaussQuadratur.ggb
|
 5.5.4 Numerische Raum-Integration
5.5.4 Numerische Raum-Integration
|
Abschnitt
5.5.4.1
Seite 446
Auflage 1:
Seite 396

|
|
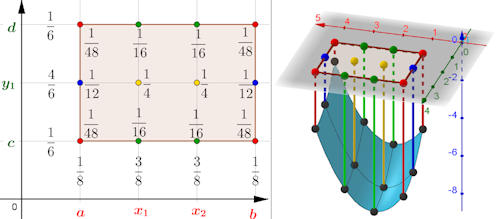
Abb. 5.40 Raumintegral
numerisch über ein Rechteck.
\(\int_{[a,b]\times[c,d]} f(x,y)\, {\rm d} x\,{\rm d} y\) für
\(f(x,y)=(x-2)^2+\frac{1}{2}(y-3)^2-7\).
Bezüglich \(x\) wird die Drei-Achtel-Regel, bzgl.
\(y\) die Kepler'sche Regel verwendet. Die Gewichte für die Punkte im Rechteck
ergeben sich als die Produkte der Gewichte für die einzelnen Variablen.
Z.B. ist das Gewicht zu \((x_1,y_1)\) gegeben als
\(\frac{3}{8}\cdot\frac{4}{6} = \frac{1}{4}\). Gleiche Gewichte
haben gleiche Farben. Die Realisierung und die Rechnungen in diesem Fall,
erstellt mit GeoGebra, finden Sie im folgenden Zusatz.
 RaumintegralRechteck.ggb
RaumintegralRechteck.ggb
|
 Zusatz Zusatz
Abschnitt 5.5.4.1
Seite 446
Auflage 1:
Seite 396
|
Der wahre Wert des Integrals errechnet sich zu
\[
\int_1^3\int_1^4 f(x,y)\,{\rm d} x\,{\rm d} y = -32.
\]
Für die numerische Integration brauchen wir zunächst eine Wertetabelle:
\[
\begin{array}{r|c|c|c|c|}
f(x,y) & x=1 & 2 & 3 & 4 \\
\hline
y=1 & -4.0 & -5.0 & -4.0 & -1.0 \\
\hline
2 & -5.5 & -6.5 & -5.5 & -2.5 \\
\hline
3 & -6.0 & -7.0 & -6.0 & -3.0 \\
\hline
\end{array}
\]
Damit erhält man für die Näherung
\[
\int_1^3\int_1^4 f(x,y)\,{\rm d} x\,{\rm d} y \approx
(4-1)\cdot(3-1)\cdot
\begin{pmatrix}
-4.0 \cdot\frac{1}{48} -5.0 \cdot\frac{1}{16} -4.0
\cdot\frac{1}{16} -1.0\cdot\frac{1}{48} \\
-5.5 \cdot\frac{1}{12} -6.5 \cdot\frac{1}{4}\ -5.5
\cdot\frac{1}{4}\ -2.5\cdot\frac{1}{12} \\
-6.0 \cdot\frac{1}{48} -7.0 \cdot\frac{1}{16} -6.0
\cdot\frac{1}{16} -3.0\cdot\frac{1}{48} \\
\end{pmatrix}
= -32
\]
die natürlich exakt ist, weil der Polynomgrad kleiner als 3 ist.
|
Abschnitt
5.5.4.2
Seite 447
Auflage 1:
Seite 397

|

|
Abb. 5.41 Raumintegral
numerisch über ein achsenparalleles Dreieck. a) Stützpunkt ist der
Dreiecksschwerpunkt, d.h. der Schnitt der Seitenhalbierenden. b) Die
Stützpunkte liegen auf den Seitenmitten. c) Der blaue Stützpunkt ist
der Schwerpunkt. Die grünen Punkte sind drei Punkte eines Rechtecks mit
linker unterer Ecke \(\frac{9-2\sqrt{15}}{21}(h,k)\) und rechter
oberer Ecke \(\frac{6+\sqrt{15}}{21}(h,k)\), die roten Punkte sind
drei Punkte eines Rechtecks mit linker unterer Ecke
\(\frac{6-\sqrt{15}}{21}(h,k)\) und rechter oberer Ecke
\(\frac{9+2\sqrt{15}}{21}(h,k)\); beide Male gehört eine Rechteckecke
nicht zu den Stützstellen. Die zugehörigen Gewichte sind eingetragen.
 RaumintegralDreieck.ggb
RaumintegralDreieck.ggb
|
Abschnitt
5.5.4.2
Seite 448
Auflage 1:
Seite 398

|
|
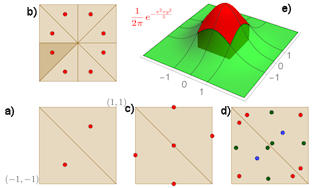
Abb. 5.42 Beispiel für ein Raumintegral.
Das Integral
\(\int_{-1}^1\int_{-1}^1 \frac{1}{2\pi}{\rm e}^{-\frac{1}{2}(x^2+y^2)}\,{\rm d} x\,{\rm d} y\)
wird auf vier Weisen numerisch berechnet. Der richtige Wert ist \(0.466065\),
als Näherungen ergeben sich
a) \(0.569672\), b) \(0.485574\),
c) \(0.469626\), d) \(0.466559\).
Hier sieht man beim Vergleich von b) und c), dass mit weniger Punkten und
verbesserter Fehlerordnung eine höhere Genauigkeit erzielt wird.
 RaumintegralBsp.ggb
RaumintegralBsp.ggb
|
 5.6 DGLn numerisch lösen
5.6 DGLn numerisch lösen
|
| | In den Abb. 5.35 bis 5.44 sind alle als "Lösung" bezeichneten Kurven mit GeoGebra numerisch erzeugt, und zwar mit dem Runge-Kutta-Verfahren.
Abschnitt 5.6.5 zeigt den Aufwand für die exakten Lösungen in Abb. 5.45.
In den folgenden Dateien ist das Richtungsfeld ein Bild. Das in GeoGebra verfügbare Richtungsfeld besteht nur aus Strichlein.
Aber bei Abb. 5.44 (und folgende) haben wie ein für alle
DGLn 1. Ordnung nutzbares schönes Richtungsfeld in GeoGebra verwirklicht.
|
Abschnitt
5.6
Seite 448
Auflage 1:
Seite 399

|

|
Abb. 5.43 Untersuchungen zum
Richtungsfeld von \(y'=y^2-x=f(x,y)\).
a) Richtungsfeld mit zwei auffälligen Kurven.
b) Richtungsfeld mit Isoklinen für \(m=\)
\(2,\,0,\,-2,\,-4,\,-6\). Berechnung der Isoklinen bei Abb. 4.6
c) Mit dem Spurmodus von GeoGebra eingezeichnete Scharen von
Lösungskurven, die Sie hier selbst erkunden können. In der ggb-Datei sind einige davon als Folge von Lösungskruven fest realisiert.
Hervorzuheben ist die schwarze Lösung,
die die blauen und grünen Lösungen voneinander trennt. Diese ist in Abschnit 5.6.5 exakt berechnet und in Abb. 5.53 violett dargestellt.
a)  y2minusx-Richtungsfeld+eine+Loesung.ggb
y2minusx-Richtungsfeld+eine+Loesung.ggb 
b)
 y2minusx-isoklinen.ggb
y2minusx-isoklinen.ggb 
c)  y2minusx-isoklinen+Loesung.ggb
y2minusx-isoklinen+Loesung.ggb 
|
Abschnitt
5.6
Seite 449
Auflage 1:
Seite 400

|
|
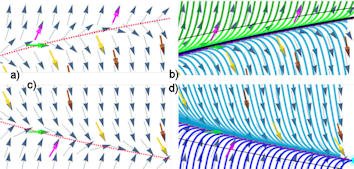
Abb. 5.44 Richtungsfeld von
\(y'=y^2-x=f(x,y)\).
a) Nullisokline, sowie farblich hervorgehobene Richtungsvektoren aus
anderen Isoklinen,
b) die grünen und die blauen Lösungskurven, werden exakt von der Grenzlinie getrennt, die in Abb. 5.54 violett eingetragen ist. In deren Nähe werden die Lösungen (von links nach rechts gesehen) gestreut.
Die blauen Lösungskurven haben alle einen Scheitel auf der Nullisokline, von dort an ist ihre Farbe hellblau und sie haben diese Nullisokline auch als als Asymptote. Deren Nähe werden die die hellblauen Lösungen gesammelt.
a) siehe oben
b) y2minusx-isoklinen+Loesung.ggb
y2minusx-isoklinen+Loesung.ggb 
|
 5.6.1 Eulerverfahren
5.6.1 Eulerverfahren
|
Wichtiger Hinweis für die *.ggb. Dateien von Abbildungen 5.45 bis 5.51:
Beim Ändern der Schrittweite h werden oft falsche Graphen angezeigt.
Mit Strg r muss man eine Neuberechnung erzwingen . |
|
Abschnitt
5.6.1
Seite 451
Auflage 1:
Seite 401

|
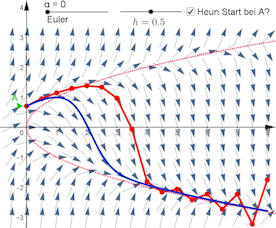
|
Abb. 5.45 Eulerverfahren
für \(y'=y^2-x\).
Schrittweite ist
\(h=0.5\), Anfangswerte sind \(y(0) = 0.7\),
also ist \(A=P_0=(0,\,0.7)\).
Es folgen
\(P_1=(0.5,\,0.945), P_2=(1.0,\,1.142)\dots\)
Ab etwa \(x=4\) ist die blaue
Lösungskurve recht dicht an der (rot gepunkteten) Nullisokline.
Wenn ein Eulerschritt diese nach unten überschreitet, wird der nächste Schritt
nach oben gehen. Im Bild wechseln nun positive und negative Steigungen. Man
beachte aber, dass die blaue Lösung rechts niemals wieder Steigung null haben
wird, sie liegt stets über der Nullisokline. Das Eulervefahren "entgleist" hier.
 y2minusx-Euler.ggb
y2minusx-Euler.ggb 
Kleiner Trick: Es wird mit dem Schieberegler eigentlich \(n\) gesteuert und daraus dann \(h=2^{-n}\) bestimmt.
|
Abschnitt
5.6.1
Seite 452
Auflage 1:
Seite 402

|
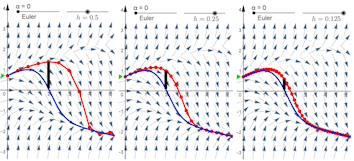
|
Abb. 5.46 Eulerverfahren für
\(y'=y^2-x\).
Schrittweiten sind \(h=0.5,\ 0.25,\ 0.125\), Anfangswerte wieder
\(y(0) = 0.7\). Die schwarzen Balken dokumentieren die Halbierung
des globalen Fehlers an der Stelle 2 bei Halbierung der Schrittweite.
In der Datei (=vorige) ist der Fehlerbalken einzuschalten.
 y2minusx-Euler.ggb
y2minusx-Euler.ggb 
|
Abschnitt
5.6.2
Seite 454
Auflage 1:
Seite 405

|
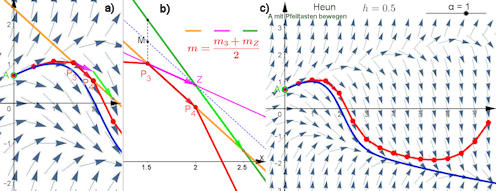
|
Abb. 5.47 Heunverfahren für
\(y'=y^2-x\) schrittweise und im ganzen Verlauf.
a) ist ein
Ausschnitt aus c), und b) zeigt den in a) sichtbaren 4. Verfahrensschritt vergrößert im
zweiten Grafikfenster von GeoGebra.
Daraus sind \(P_3\), \(P_4\) und die Richtung nach
\(P_4\) (orange) aus der Konstruktion in b) übertragen worden und demonstrieren
die Korrektheit des geometrischen Verfahrens.
Speziell b): Mit der in \(P_3\) gültigen (lila) Pfeilrichtung erreicht man im
Abzissenabstand \(h=0.5\) den Zwischenpunkt \(Z\), in dem die durch den hellgrünen
Vektor bzw. die grüne Gerade gezeigte Richtung gilt. Der Mittelwert der beiden
Geradensteigungen ist hier geometrisch durch die durch \(M\) gemittelte Strecke
und die blau-gestrichelte Gerade \(MZ\) visualisiert.
Auf einer Parallelen zu ihr durch \(P_3\) erreicht man an der Abszisse von \(Z\)
Punkt \(P_4\).
 y2minusx-Heun.ggb
y2minusx-Heun.ggb 
|
| |
In c) ist ein Bild einer
"multifunktionalen" GeoGebra-Datei gezeigt.
Hier können Sie nicht nur die
Schrittweite \(h\) und den Start \(A\)
steuern, sondern mit \(\alpha\) mehrere der im Folgenden dargestellten Verfahren
auswählen. Hier gilt \(\alpha=1\) und \(A:\, y(0) = 0.7\). Vergleichen Sie mit dem
Eulerverfahren Abb. 5.45, das man mit \(\alpha=0\) erhält, und
mit dem modifizierten Eulerverfahren in Abb. 5.49, das
\(\alpha=0.5\) erfordert.
 y2minusx-Heun-mit-alpha.ggb
y2minusx-Heun-mit-alpha.ggb 
|
 5.6.2 HeunVerfahren
5.6.2 HeunVerfahren
|
Abschnitt
5.6.2
Seite 455
Auflage 1:
Seite 405

|
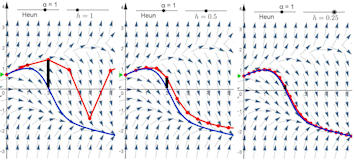
|
Abb. 5.48 Heunverfahren für
\(y'=y^2-x\).
Schrittweiten sind \(h=1,\ 0.5,\ 0.25\). Drei Fehlerbalken sind
hervorgehoben und zeigen, dass sich der globale Fehler viertelt, wenn
die Schrittweite halbiert wird. Vergleichen Sie mit
Abb. 5.46.
In der Datei (=vorige) ist die Fehlergerade einzuschalten.
 y2minusx-Heun-mit-alpha.ggb
y2minusx-Heun-mit-alpha.ggb 
|
Abschnitt
5.6.2.2
Seite 457
Auflage 1:
Seite 408

|
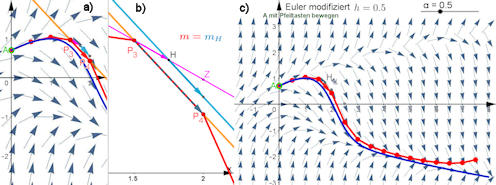
 y2minusx-Euler-modi.ggb
y2minusx-Euler-modi.ggb 
 y2minusx-Euler-modi-mit-alpha.ggb
y2minusx-Euler-modi-mit-alpha.ggb 
|
Abb. 5.49 Modifiziertes Eulerverfahren
\(y'=y^2-x\) schrittweise und im gesamten Verlauf.
a) und b) Der Schritt von \(P_3=(1.5,0.964)\) nach \(P_4\) wird genau
betrachtet. Zum Zwischenpunkt \(Z\) (violett) gelangt man mit einem Eulerschritt
mit \(m_3=f(x_3,y_3)\).
Der Hilfspunkt \(H\) auf der Hälfte der Strecke \(\overline{P_3 Z}\) ist
\(H=(x_3+\frac{h}{2}, y_3+m_3\cdot\frac{h}{2})\). Dort hat das Richtungfeld die
Steigung \(m_H=f(x_H,y_H)\) (hellblau).
Mit dieser Steigung vollzieht man einen ganzen Eulerschritt
und gelangt zu \(P_4=(x_3+h,y_3+m_H\cdot h)\).
b) zeigt
dieses Vorgehen in größerem Maßstab im zweiten Grafikfenster von GeoGebra. Die
gelbe Gerade und \(P_4\) sind in das Hauptfenster a) übertragen worden. Man
erkennt die übereinstimmung.
c) Gesamtverlauf mit Startpunkt
\(A\colon\ y(0)=0.7\). Vergleichen Sie mit Abb. 5.45,
Abb. 5.47 c) und
Abb. 5.51 b).
|
 5.6.3 Numerische Integration liefert Verfahren für DGLn
5.6.3 Numerische Integration liefert Verfahren für DGLn
|
Abschnitt
5.6.3
Seite 459
Auflage 1:
Seite 410

|
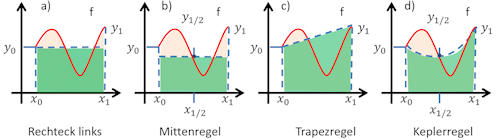
|
Abb. 5.50 Einsatz von
numerischer Integration für DGLn.
a) Riemann'sche Summe \(\to\) Eulerverfahren,
b) Mittenregel \(\to\) modifiziertes Eulerverfahren,
c) Trapezregel \(\to\) Heunverfahren,
d) Kepler'sche Regel \(\to\) ? Lesen Sie den
Text im Buch!

|
 5.6.4 RungeKutta-Verfahren
5.6.4 RungeKutta-Verfahren
|
Abschnitt
5.6.4
Seite 460
Auflage 1:
Seite 411

|
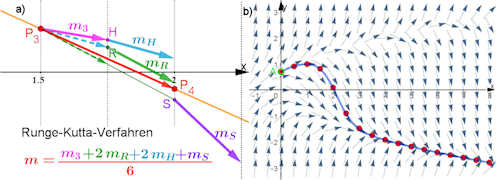
|
Abb. 5.51 Runge-Kutta-Verfahren.
a) Skizze eines Schrittes von \(P_3\) aus:
Die Hilfspunkte werden in folgender Reihenfolge aufgesucht:
Mit \(m_3\) (lila) einen halben Eulerschritt zu \(H\), dort findet
man \(m_H\) (hellblau).
Mit \(m_H\) einen halben Eulerschritt zu \(R\), dort findet
man \(m_r\) (grün).
Mit \(m_r\) einen ganzen Eulerschritt zu \(S\), dort findet
man \(m_s\) (violett).
Der Zielpunkt \(P_4{=}(x_4,y_4)\) wird mit einem ganzen
Eulerschritt erreicht (rot), bei dem man
\(m = \frac{1}{6}(m_3+2m_H+2m_R+m_S)\) verwendet.
b) Die Punkte des Runge-Kutta-Verfahrens
liegen praktisch perfekt auf der Lösungskurve.
 y2minusx-RungeKutta.ggb
y2minusx-RungeKutta.ggb
|
Abschnitt
5.6.4
Seite 461
Auflage 1:
Seite 411

|
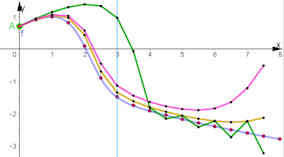
|
Abb. 5.52 Numerische DGL-Verfahren für
\(y'=y^2-x\) im Vergleich mit \(h=0.5\).
Der exakte Wert (blau) an der Stelle \(x=3\) ist \(y(3)=-1.47393\).
Das Runge-Kutta-Verfahren (rot) bringt: \(y(3)\approx -1.50044\), das ist ein
Fehler von nur \(1.4\%\).
Modifiziertes Eulerverfahren (ocker): \(y(3)\approx -1.3515\),
Heun (lila): \(y(3)\approx -1.1338\),
Euler (grün): \(y(3)\approx 0.9641\).
\(A\) ist beweglich.
 y2minusx-alle-Vergleich-Pfeile.ggb
y2minusx-alle-Vergleich-Pfeile.ggb 
 y2minusx-alle-Vergleich.ggb
y2minusx-alle-Vergleich.ggb 
|
 5.6.5 Skurrile DGLn
5.6.5 Skurrile DGLn
|
Abschnitt
5.6.5
Seite 462
Auflage 1:
Seite 412

|
|
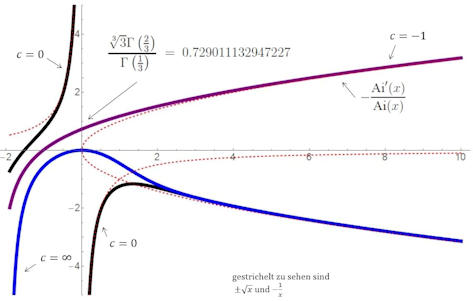
Abb. 5.53 \(y'=y^2-x\) exakt gelöst.
Eine Vielzahl von numerisch bestimmen Lösungen ist in Abb.5.53 und 5.54 dargestellt.
 Lösung-y'=y2-x, Mathematica Quelltext
Lösung-y'=y2-x, Mathematica Quelltext
 Dies zum Lesen und Verstehen Dies zum Lesen und Verstehen
|
Abschnitt
5.6.5
Seite 463
Auflage 1:
Seite 413

|
|
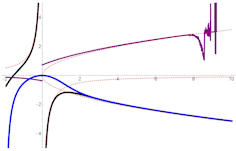
Abb. 5.54 \(y'=y^2-x\) exakt
gelöst, aber numerisch ungenau. Wenn man statt der Airy-Funktionen die
ursprünglichen Besselfunktionen verwendet, gerät selbst Mathematica hier
offenbar in numerische Schwierigkeiten, wie man am rechten Bildrand deutlich
sieht. Auch ist diese "Lösungskurve" bei \(x=0\) plötzlich unstetig.
Tatsächlich wurden hier die Realteile der scheinbar komplexen Lösungen
gezeichnet, was aber am Ergebnis nichts ändern dürfte, da die Lösungen ja
eigentlich reell sind.
 Lösung-y'=y2-x, Mathematica Quelltext
Lösung-y'=y2-x, Mathematica Quelltext
 Dies zum Lesen und Verstehen Dies zum Lesen und Verstehen
|
 5.6.6 Weitere Methoden und Aspekte
5.6.6 Weitere Methoden und Aspekte
|
 5.6.6.1 Implizite Verfahren 5.6.6.1 Implizite Verfahren |
 5.6.6.2 Mehrschritt- Verfahren
5.6.6.2 Mehrschritt- Verfahren
|
|
Abschnitt
5.6.6.2
Seite 465
Auflage 1:
Seite 415

|

Bei allen ist nur des Bild anzusehen. 
|
Abb. 5.55 Mehrschrittverfahren
veranschaulicht. a) explizites Mehrschrittverfahren,
der rote Punkt ergibt sich aus Formel 5.1,
b) implizites Mehrschrittverfahren, \(p_{n+1}\) wird mit
unbekanntem \(y_1\) aufgestellt,
c) leapfrog-Verfahren. Bei letzterem ist der Integrationsbereich
ein anderer, nämlich von \(x_{-1}\) bis \(x_1\). Das Integral wird durch die
Mittenregel approximiert, weshalb nur \(f(x_0,y_0)\) in die Rechnung eingeht.
 DGLnumMehrschritt1.ggb
DGLnumMehrschritt1.ggb
 DGLnumMehrschritt2.ggb
DGLnumMehrschritt2.ggb
 DGLnumleapfrog3.ggb
DGLnumleapfrog3.ggb
|
5.6.6.3 Systeme von DGLn |
 5.6.6.4 Stabilität und steife DGLn
5.6.6.4 Stabilität und steife DGLn
|
Abschnitt
5.6.6.4
Seite 466
Auflage 1:
Seite 417

|
|
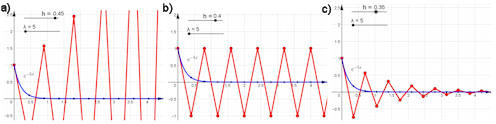
Abb. 5.56 Das Eulerverfahren ist
instabil. Die DGL \(y' = -\lambda y\)
zu den Anfangswerten \(y(0) =1\) hat die exakte Lösung \(y(x) = {\rm e}^{-\lambda x}\).
Sie wird mit dem Eulerverfahren approximiert. Im Bild ist \(\lambda = 5\).
In a), b), c) sind die Schrittweiten
\(h=0.45,\ 0.4,\ 0.35\). Bei \(h>0.4\) wird das Verfahren instabil!
 DGLnumEulerinstabil.ggb
DGLnumEulerinstabil.ggb 
|