Mathematik sehen und verstehen,Website zum Buch

Höhere Mathematik sehen und verstehen
ISBN 978 662 69291 2 Auflage 2   Book         Springer Spektrum
ISBN 978 662 69292 9 Auflage 2 eBook
www.mathematik-sehen-und-verstehen.de
https://masuv.web.leuphana.de     (Sicherer Zugang)

Dörte Haftendorn

Dieter Riebesehl

Hubert Dammer

Anhang: 6 Geometrie und 7 Werkzeuge

Im Buch haben wir im Anhang die 6 Geometrie und die 7 Werkzeuge zusammengefasst, hier führen wir sie als Kapitel 6 und 7.
7 Werkzeuge:	GeoGebra	Mathematica+WolframAlpha	Ti-Nspire	Surfer	Weitere: Cinderella,...
ALLE BILDER (außer den Icons) erscheinen beim Anklicken in neuem Tab in dreifacher Größe.

GeoGebra https://www.geogebra.org
Abschnitt 6.3.1 Seite 426	Zu dem Ende 2020gültigen Stand der rasanten GeoGebra-Entwickung lesen Sie am Besten im Buch. Auf weitere wesentliche Neuerungen ab 2021 werden wir an dieser dieser Stelle berichten. Insbesondere ist zu erwarten, dass die GeoGebra-Rechnersuite als übergreifendes Tool entwickelt wird.
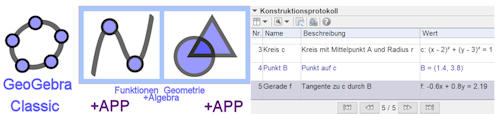
Abschnitt 6.3.1 Seite 427		Abb. 6.10 GeoGebra Classic. Im Grafikfenster sind sowohl Funktionen als auch direkt dort definierte geometrische Objekte zu sehen. In einem Algebrafenster werden Namen und Werte der Objekte angezeigt. Zudem ist ein Konstruktionsprotokoll einsehbar und eine Navigationsleiste, mit der man die Schritte nacheinander im Grafikfenster sehen kann. Dies ermöglicht das Verstehen fer- tiger GeoGebra-Dateien. Weiter gibt es ein zweites Grafikfenster mit denselben Möglichkeiten. In diesem Buch ist das an einigen Stellen genutzt, denn es erlaubt Eigen- schaften der Objekte in zwei Aspekten grafisch zu koppeln.
Abschnitt 6.3.1 Seite 427		Abb. 6.11 GeoGebra Classic und Apps. Die nächsten vier Fenster sind ebenfalls in GeoGebra classic enthalten, Beschreibung im Text. Die Möglichkeiten eines WTR bzw. GTR (wissen- schaftlichen bzw. grafikfähigen Taschenrechners) sind in zwei speziellen Apps verwirklicht. Ein Prüfungsmodus ist für alle Tablet- und Handy-Apps, aber auch für GeoGebra Classic ver- fügbar, um einen kontrollierbaren Einsatz u.a. im Abitur zu ermöglichen.
	Die vier ersten Fenster in Abb. 6.11 erlauben: 1.) 3D-Konstruktionen und 3D- Raumflächen, 2.) im CAS symbolische Umformungen und Gleichungslösungen, 3.) in einem Tabellenkalulationsfenster Rechnen mit Listen und Definition von Matrizen. 4.) Im Wahrscheinlichkeitsfenster werden zu fast allen gängigen Verteilungen Gra- phen zur interaktiven Betrachtung des Hypothesentestens angeboten.

	Wir haben uns vorgenommen, hier die GeoGebra-Hilfen speziell bezogen auf unser Buch zu geben. Dabei wollen wir auch Links zu den Stellen auf dieser Website setzen, an denen wir schon Besonderheiten erklärt haben. Das wird aber nicht so schnell klappen . Darum verlinken wir hier erstmal die : GeoGebra-Hilfen und Softwarehinweise aus dem Kurvenbuch
Weitere hilfreiche mathematische Werkzeuge Im Buch ist dies Abschnitt 6.3.2.
7.4 Raumgeometrie, spez. Surfer
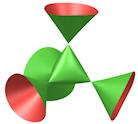
Abschnitt 6.3.2.1 Seite 428		Abb. 6.12 Surfer zeichnet algebraische Raumflächen. \(x^2+y^2+z^2+2xyz-1=0\). Man kann damit Raumflächen zu Polynomgleichungen in \(x,\,y,\,z\) darstellen. Dieses frei verfügbare Programm wurde genau für implizite kartesische Gleichungen von Raumflächen von Dr. Oliver Labs im Mathematik-Jahr 2008 für das renommierte internationale mathematische Forschungsinstitut in Oberwolfach entwickelt, siehe https://imaginary.org/program/surfer.
7.2 Mathematica und Wolfram\|Alpha
	Kostenloses Tool ist: https://www.wolframalpha.com/	Wolfram_Alpha_ Wissen der Welt berechenbar.htm FAQ-Seite von Wolfram\|Alpha (hier für Sie einegfügt.)
7.3 Ti-nspire und andere CAS Taschenrechner
Abschnitt 6.3.2.3 Seite 428	Mit dem TI-Nspire-CAS als Taschenrechner haben wir viel Erfahrung. Die im Buch beschriebenen Konstruktionen und CAS-Rechnungen sind auch alle mit dem "`Handheld"' zu bewältigen. Auf der Website \cite{HaftendornW1} finden Sie viele TI-Nspire-Dateien zum Herunterladen, sie sind kenntlich an einem Button *.tns. Die Möglichkeiten, Farben, Strichdicken, Beschriftungen und anderes zu steuern, sind nicht so komfortabel wie in GeoGebra. Aber die Verfügbarkeit in der Hand der Lernenden ist didaktisch "`Gold wert"'.
Beispiel zu Abschnitt 5.3.3 Seiten 369-370	Diese ist ein Ausschnitt aus einer einer acht Seiten umfassenden Lernsequenz, die vollstädig mit Grafiken, Text, CAS-Berechnungen und Erkundungen im CAS-Taschenrechner TI-nspire möglich sind.	Hier demonstrieren wir, dass es für das Lernen und Verstehen fördenlich sein kann, mehrere Werkzeuge und Darstellungsarten zu verwenden. Sie finden die abgebildete Zusammenstellung auf der Seite Numerik von www.mathematik-verstehen.de Sie sehen links das Gerüst für Bézier-Splines und die Herleitung, wie sie im TI-nspire in den Fenstern direkt im CAS mit den Ergenbissen gemacht werden kann. Dieser CAS-Taschenrecher hat, wie auch GeoGebra, mehrere Fenster. Diese bilden dann aber nicht nur eine Datei .tns, die man transportieren, senden, wieder öffnen und bearbeiten kann. Sondern sie können ähnlich wie Powerpoint-Folien als präsentierbare Seiten in einer Pdf-Datei* gestaltet und gespeichert werden. Dadurch kann der ganze Lern- und Erstellungsprozess dokumentiert werden, was für Lernende selbst, auch für Lerngruppen, Begleitung und Beurteilung ein unschätzbarer Vorteil ist.
	Auf den Seiten dieses Webverbundes sind mit Themenname diese Pdf-Seiten angegeben, Handzettel mit acht solchen Seiten bieten eine schnelle Übersicht, und mit wird der Download der Rechnerdatei ermöglicht.
7.5 Weitere Mathematik-Software Cinderella