Höhere Mathematik sehen und verstehen ISBN 978 662 69291 2 Auflage 2   Book         Springer Spektrum ISBN 978 662 69292 9 Auflage 2 eBook www.mathematik-sehen-und-verstehen.de     https://masuv.web.leuphana.de     (Sicherer Zugang)

Dörte Haftendorn Dieter Riebesehl Hubert Dammer

Anhang: 6 Geometrie und 7 Werkzeuge

Im Buch haben wir im Anhang die kleinen Kapitel 6 Geometrie mit den wesentlichen geometrischen Grundlagen und 7 Werkzeuge mit den verwendeten Werkzeugen zusammengefasst. 6.1.1 Dreiecke 6.1.2 Kreiswinkelsätze 6.1.3 Trigonometrie 6.1.4 Pythagoras-Gruppe 6.1.5 Cosinussatz 6.1.6 Darstellende Goemetrie 6.2 Komplexe Zahlen ALLE BILDER (außer den Icons) erscheinen beim Anklicken in neuem Tab in dreifacher Größe.

	6 Geometrie	6.1.1 Besondere Punkte im Dreieck
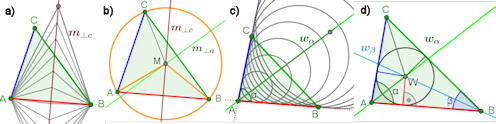
Abschnitt 6.1.1 Seite 419		Abb. 6.1 Dreiecks-Mittelpunkte. a) Mittelsenkrechten einer Strecke enthalten genau die Punkte mit gleichen Abständen zu deren Ecken. b) Sie schneiden sich im Mittelpunkt des Umkreises. c) Winkelhalbierende enthalten genau die Punkte mit gleichen Abständen zu den Schenkeln des Winkels. d) Sie schneiden sich im Mittelpunkt des Inkreises. a) dreieck-mittelsenkrechten.ggb d) dreieck-winkelhalbierenden.ggb
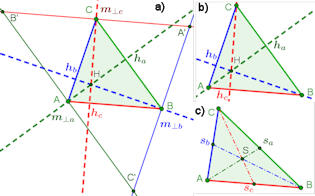
Abschnitt 6.1.1 Seite 420		Abb. 6.2 a), b) Es existiert der Höhenschnittpunkt \(H\). a) Die Beweiszeichnung ist durch Parallelen durch die Ecken so erweitert, dass die Höhen zu den Mittelsenkrechten des großen Dreiecks werden. Dadurch ist der Schnittpunkt in b) gesichert. c) Der Schwerpunkt \(S\) ist der Schnittpunkt der Seitenhalbierenden. \(S\) teilt jede Seitenhalbierende im Verhältnis 2:1 von der Ecke aus gesehen. b) erscheint zuerst, a) können Sie hinzuschalten. dreieck-besondere-hoe.ggb c) schwerpunktsatz.ggb     Beweis des Schwerpunktsatzes vektoriell in Linearer Algebra
6.1.2 Kreiswinkelsätze
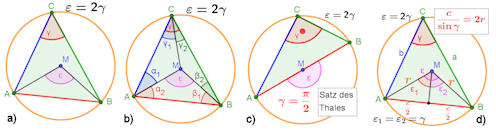
Abschnitt 6.1.2 Seite 420		Abb. 6.3 Kreiswinkelsätze. a) Umfangswinkelsatz, b) zu dessen Beweis, c) Satz des Thales, d) Sinussatz und Umkreisradius. a) dreieck-UWS.ggb b) UWS-beweis-b.ggb c) Thalessatz.ggb Mit einer interaktiven Ergänzung zur Umkehrung des Satzes d) UWS-Umkreisradius.ggb
6.1.3 Trigonometrische Beziehungen im rechtwinkligen Dreieck
6.1.4 Satzgruppe des Pythagoras
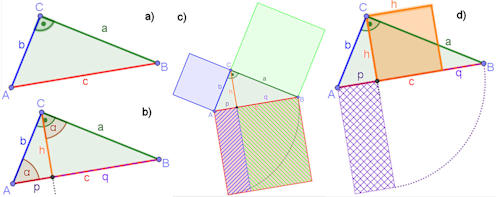
Abschnitt 6.1.4 Seite 422		Abb. 6.4 Satzgruppe des Pythagoras. a) Standardbezeichnung, Konstellation, b) Höhe und Höhenabschnitte \(p\) und \(q\), Ähnlichkeit! c) Satz des Pythagoras (unschraffiert) \(a^2+b^2=c^2\),      Kathetensatz des Euklid (schraffiert)\(b^2=pc, \ a^2=qc\) Darin sind auch die Beweise. d) Höhensatz des Euklid \(h^2=pq\) Bei allen Dreiecken ist C auf dem Thaleskreis zu ziehen. a) und b) dreieck-grund-bez.ggb c) dreieck-pyth.ggb d) dreieck-hoehensatz.ggb
6.1.5 Cosinussatz
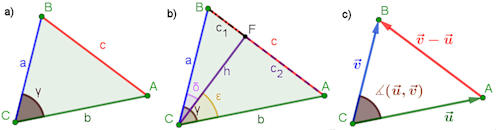
Abschnitt 6.1.5 Seite 423		Abb. 6.5 Cosinussatz. a) Konstellation für \(c^2=a^2+b^2-2ab\cos \gamma\) b) Bezeichnungen für den Beweis im Buch S. 423 c) Wie bei Abb. 2.5 verhilft uns der Cosinussatz, geschrieben mit Vektoren und Normen, zu einer geometrischen Deutung des Skalarproduktes in Satz 2.4. Der Verkrorielle Beweis ist in Abschnitt 2.1.6.1 auf Seite 142 im Buch. Anmerkung: In der vektoriellen Form sieht man deutlicher, dass man auch mit außerhalb des Dreiecks liegenden Höhen kein Problem hat. Auch Abb. 2.5 verdeutlicht dieses. cosinussatz-geo.ggb
6.1.6 Darstellende Geometrie Aspekt: Konstruktion wahrer Längen und Winkel für Körper
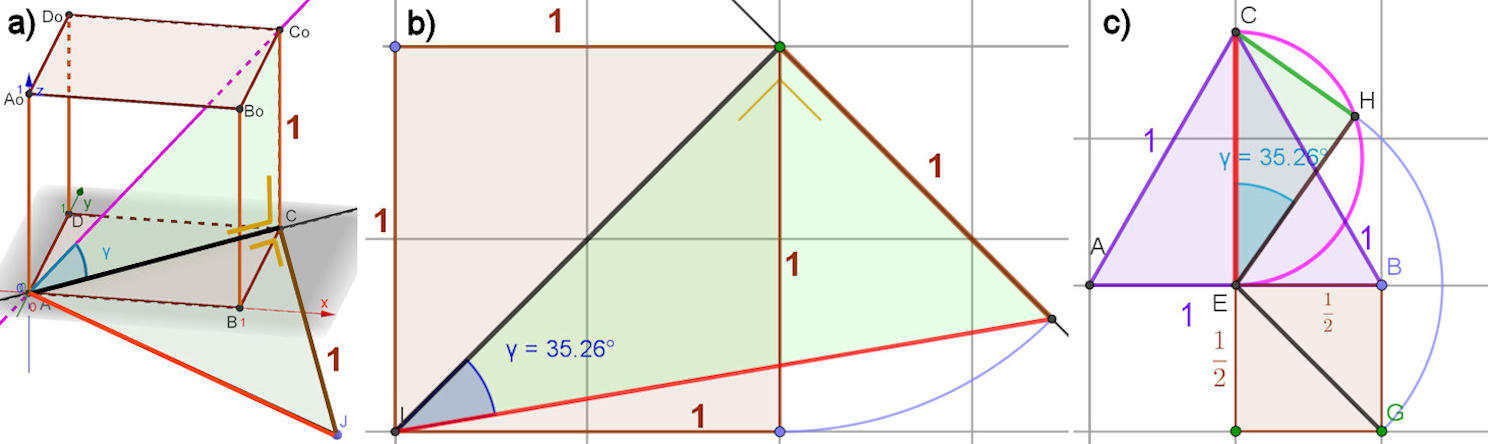
Abschnitt 6.1.6 Seite 424	Vektoriell: \(\left(\begin{array} 11\cr 1\cr 0 \end{array}\right)\cdot \left(\begin{array} 11\cr 1\cr 1 \end{array}\right)=\sqrt{2}\cdot \sqrt{3}\cos{\gamma} \Leftrightarrow \cos{\gamma}=\frac{2}{\sqrt{2}\cdot \sqrt{3}} \) Berechnungsvariante zu b) \(\tan{\gamma}=\frac{1}{\sqrt{2}}\) wuerfel3d-solo.ggb	Abb. 6.6 Winkelkonstruktion} im 3D-Würfel. a) Schrägbild mit dem in die Grundebene geklappten Diagonalebenen-Dreieck (nicht maßgerecht), damit man sich Zeichnung b) besser vorstellen kann. In der GoeGebra-Datei können Sie das Dreieck wirklich klappen. Im 3D-Fenster von GeoGebra kann man allerdings räumliche Winkel und Strecken auch direkt messen. Insofern sind solche Methoden der Darstellenden Geometrie historisch. b) entsprechend a) in wahren Längen. Man kann nun die (rote) Raumdiagonale und den Diagonalenwinkel sowohl messen als auch berechnen. c) Gesucht ist der Winkel, den die Raumdiagonale der Länge \(\sqrt{3}\) als Hypotenuse und \(\sqrt{2}\) als Kathete bilden. Weil die Höhe im gleichseitigen Dreieck \(\frac{1}{2}\sqrt{3}\) ist, nehmen wir auch \(\frac{1}{2}\sqrt{2}\) als Quadratdiagonale und verwenden sie mit dem Thalessatz als Kathete. Das Ergebnis \(\gamma=\arccos\big(\frac{\sqrt{2}}{\sqrt{3}}\big)\approx 35.26^\circ\) wird von GeoGebra aus der Zeichnung intern mit gewünschter Genauigkeit berechnet. Eine solche Konstruktion steht hier nur prototypisch für historische Vorgehensweisen.
6.2 Geometrische Aspekte der komplexen Zahlen
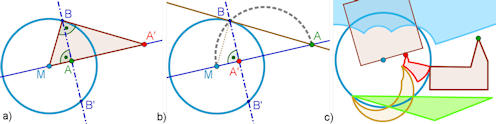
Abschnitt 6.2.1 Seite 425	inversion-k-A-innen.ggb inversion-objekte.ggb inversion-k-A-aussen.ggb	Abb. 6.7 Kreisspiegelung = Inversion am Kreis mit dem Mittelpunkt \(M\) und dem Radius \(k\). a) Abbildung eines Punktes \(A\) im Innern des Inversionskreises: Senkrechte auf \(MA\), in einem Schnittpunkt mit dem Kreis Tangente als Senkrechte auf dem Radius, Schnittpunkt von Tangente und \(MA\) ist der Bildpunkt \(A'\). b) Umgekehrt: Abbildung eines Punktes \(A\) außerhalb des Inversionskreises: Thaleskreis auf \(\overline{MA}\), im Schnittpunkt Lot auf \(MA\) fällen, der Lotfußpunkt ist der Bildpunkt \(A'\). \(\overline{AB}\) ist Tangente. c) Mit dem Button "Kreisspiegelung" werden Polygone (Kirche, Quadrat, Dreieck) am blauen Kreis gespiegelt.
Zusatz	Eigenschaften der Kreisspiegelung Bei der Kreispiegelung an einem Kreis mit dem Radius \(k\) und Mittelpunkt \(M\), bei dem \(A'\) das Bild von \(A\) ist, gilt: \(\overline{MA}\cdot\overline{MA'}=k^2\). Beweis: Dies gilt wegen des Kathetensatzes, in Abb. 6.7 a) ist die Kathete \(\overline{MB}=k\). q.e.d. Die Kreisspiegelung ist involutorisch, d.h. doppelte Anwendung ist die Identität. Geraden, die nicht den Ursprung enthalten, werden auf Kreise durch den Ursprung abgebildet und umgekehrt. Geraden durch den Ursprung sind Fixgeraden, aber nicht Fixpunktgeraden. Kreise, auf deren Rand nicht der Urspung liegt, werden auf Kreise abgebildet. Der Spiegelungskreis ist der einzige Fixpunktkreis. Schneidet das Urbild den Spiegelungskreis, dann sind die Schnittpunkte auch Fixpunkte. inversion-kreise+geraden.ggb
Abschnitt 6.2.1.1 Seite 425	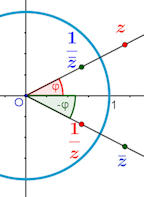Abb. 6.8 Inversion komplex. In der Gauß'schen Zahlenebene unterscheiden wir geometrisch inverse Punkte \(Z,\,Z'\) bzw. \(\bar{Z},\,\bar{Z}'\) und algebraisch inverse Zahlen \(z,\,\frac{1}{z}\) bzw. \(\bar{z},\,\frac{1}{\bar{z}}\). Erstere liegen nach Konstruktion Abb. 6.7a) auf je einem Strahl \(\overrightarrow{OZ}\) bzw. \(\overrightarrow{O\bar{Z}}\). Für algebraisch inverse Zahlen muss gelten \(z\cdot z^{-1}=1\), in der Polardarstellung ist das \((r\,{\rm e}^{{\rm i}\varphi})\cdot (\frac{1}{r}\,{\rm e}^{-{\rm i}\varphi})=1\). Um die algebraisch inverse Zahl von \(z\) geometrisch zu finden, muss zunächst ihre konjugiert komplexe Zahl \(\bar{z}\) auf dem an der reellen Achse gespiegelten Strahl \(\overrightarrow{O\bar{Z}}\) gebildet und diese dann geometrisch invertiert werden. Es ist nämlich nach obiger Formel \(1 = \overline{OZ}\cdot \overline{OZ'} = \overline{OZ\vphantom{ \bar{Z}}}\cdot \overline{O\bar{Z}'} = r\cdot\frac{1}{r}\), da \(|Z'|=|\bar{Z}'|\) gilt. Weiter ist zu sehen, dass \(\bar{z}^{\,-1}\) geometrisch invers zu \(z\) ist. Der Ursprung \(O\) hat, wie zu erwarten war, im Endlichen keinen inversen Punkt. Auf der Riemann'schen Zahlenkugel ist sein Bild aber der Nordpol. inversion-komplex-invers.ggb
Abschnitt 6.2.2 Seite 476 1.Auflage Seite 426	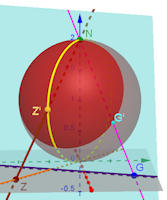Abb. 6.9 Die Riemann'sche Zahlenkugel steht wie gezeigt auf dem Ursprung der Gauß'schen Zahlenebene. Ein Punkt \(G\) der Ebene wird durch eine Gerade zum Nordpol \(N\) eineindeutig auf \(G'\) auf der Riemann'schen Zahlenkugel abgebildet. Eine Gerade und der Nordpol \(N\) definieren eine (hellblaue) Ebene, die die Kugel in einem Kreis schneidet. Dieser ist das Bild der Geraden. Eine Gerade durch den Ursprung \(O\) und \(Z\) wird auf einen (gelben) Großkreis durch den Nordpol \(N\), den Südpol \(O\) und \(Z'\) abgebildet, bis auf den Nordpol selbst. Man kann das so sehen, dass \(N\) das Bild eines unendlich fernen Punktes "\(\infty\)" ist. Anmerkung: Der Großkreis und die Geraden sind Parameterkurven im Raum. man erzeugt sie aber interaktiv durch "Kreis durch drei Punkte" u.s.w. Im Algebrafenster kann man dann dennoch die Gleichungen sehen und daraus lernen. riemann-zahlenkugel.ggb

Dies ist dieWebsite zum Buch: Höhere Mathematik sehen und verstehen START und TIPPS Liste der Zusätze 06 Geometrie 07 Werkzeuge Erstellt: Dez.2020, Update 30. August 2024
Prof. Dr. Dörte Haftendorn	Prof. Dr. Dieter Riebesehl	Dipl.-Math. Dipl.-Ing. Hubert Dammer