Höhere Mathematik sehen und verstehen ISBN 978 662 69291 2 Auflage 2   Book         Springer Spektrum ISBN 978 662 69292 9 Auflage 2 eBook www.mathematik-sehen-und-verstehen.de     https://masuv.web.leuphana.de      (Sicherer Zugang)

Dörte Haftendorn Dieter Riebesehl Hubert Dammer

Lösungen der Anregungen in Kapitel 5    Anregungen Anregung 5.1 Heronverfahren für höhere Exponenten Anregung 5.3 NURBS-Erkundung für Einheitskreise Anregungen und Lösungen Anregung 5.2 Rationale Parametrisierung für den EK Anregung 5.4 2. Metamorphose der Trisektrix

Anregung 5.1 Abschnitt 5.3.5.1 Seite 397		5.1 (Heron-Verfahren für höhere Wurzeln) Ein Vorschlag für eine Verallgemeinerung des Heronverfahrens zur Berechnung von \(\sqrt[k]r\) ist die Rekursion \( x_{n+1}=\frac{1}{2}\left(x_n+\frac{r}{x_n^{k-1}}\right)\). Berechnen Sie den Fixpunkt und untersuchen Sie die Konvergenz bzw. Divergenz. Erhält man dasselbe, wenn man stattdessen wieder mit dem Newtonverfahren arbeitet? Variieren Sie in der obigen GeoGebra-Datei das \(k\) und sehen Sie sich die Entwicklung der Treppchen an. heronRekursiv-anreg.ggb Ergänzende Informationen und Fragen www.mathematik-verstehen.de		Lösung zu 5.1 Berechnung des Fixpunktes: Trägerfunktion ist \( f(x)=\frac{1}{2}\left(x+\frac{r}{x^{k-1}}\right) \)  Schnitt mit der Winkelhalbierenden \(y=x\): \( \frac{1}{2}\left(x+\frac{r}{x^{k-1}}\right)=x \; \rightarrow \; \frac{1}{2}\frac{r}{x^{k-1}}=\frac{1}{2}x \; \rightarrow r=x^k \; \rightarrow \;x =\sqrt[k]{x} \) 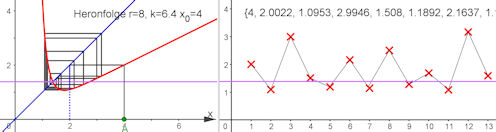Hier also \( x_{Fix}=\sqrt[6.4]{8}=1.3839\) markiert durch die violette Waagerechte. Links ist die Treppendarstellung der rekursiven Folge, rechts die Zeitdarstellung, wie bei Abb. 1.8 erläutert. Der Fixpunkt ist "nicht anziehend", also "abstoßend", wir rechnen dieses gleich nach. Entscheidend ist die Steigung der Tangente der Trägerfunktion im Fixpunkt. \( f'(x)= \frac{1}{2}\left(1+(1-k)r \;x^{-k}\right) \text{ also } f(\sqrt[k]{x})= \frac{1}{2}\left(1+(1-k)r (r^\frac{1}{k})^{-k}\right)=\frac{1}{2}\left( 1+(1-k)r \cdot r^{-1}\right)= 1- \frac{k}{2})\) \(x_{Fix}\) ist anziehend für \( |1-\frac{k}{2}|< 1\) also für \(0 < \frac{k}{2} < 2\) also \(0 < k < 4\)

Anregung 5.2 Abschnitt 5.4.3.1 Seite 419		5.2 rationale Parametrisierung des EK Eine bekannte rationale Parameterdarstellung des EK ist: \begin{eqnarray} \text{Einheitskreis:}\quad \vec{K}(t) = \left(\frac{2t}{1+t^2},\frac{1-t^2}{1+t^2}\right),\ t\in (-\infty,\infty). \end{eqnarray} Versuchen Sie, diese herzuleiten, indem sie den Kreis mit einer Geradenschar durch den Punkt \(N_1=(0,1)\) schneiden. Klappt es auch mit \(N_2=(-1,0)\)? Hinweis Bei der in Abschnitt behandelten Trisektrix wird die eben genannte Technik zur Beschaffung einer Parameterdarstellung ebenfalls angewendet.   Zu \( N_1=(0,1) \) Kreis-alternativ-als-rat-Bezierspline-Typ Anreg 5.2.orig.nb Mathematica Quelltext Dies zum Lesen und Verstehen Zu \( N_1=(-1,0)\) Kreis-pos-Durchlauf-alle-Rechnungen.nb Mathematica Quelltext Dies zum Lesen und Verstehen		Lösung zu 5.2 Wir verwenden die Kreisgleichung des Einheitskreises EK: \(x^2+y^2=1\). Durch den Punkt \(N_1=(0,1)\) legen wir die Gerade \(y=\;-t\;x +1\). Das Minuszeichen ist naheliegend, weil dann bei von \(t=0\) aus wachsendem \(t\) der Schnittpunkt des Kreises mit der Geraden nach rechts wandert. \begin{align*} x^2+(-t\;x +1)^2 &=1\\ x^2+t^2x^2-2t\;x +1&=1\\ (1+t^2)x^2&=2t\;x \quad x \neq 0\\ x&=\frac{2t}{1+t^2}\\ \\ y&=-t\frac{2t}{1+t^2}+1\\ y&=\frac{1-t^2}{1+t^2} \end{align*} Visualisierung der Parameterdarstellung In Grün und Blau sind die Funktionen \(f(t)=x(t) \text{ und }g(t)=y(t) \) dargestellt. Mit Senkrechten und Parallelen wird der Punkt \(P=(x(t),\;y(t))\) konstruiert. Zieht man an \(T\), zeichnet \(P\) seine Spur. Den Südpol kann man mit der Spur nicht erreichen, weil dafür T im Unendlichen liegen müsste. Mit dem Ortslinienwekzeug erhält man sofort den ganzen Kreis. GeoGebra nimmt intern ein größeres Intervall für \(t\) als der folgende Befehl: Auch der GeoGebra-Befehl Kurve(x(t), y(t),t,-20,20) zeichnet sofort den Kreis, aber mit der Lücke unten. ratParamEK+.ggb Kreis-N2-pos-Durchlauf.ggb Zu der Frage: Klappt es auch mit \(N_2=(-1,0)\)? Wir verwenden wieder die Kreisgleichung des Einheitskreises EK: \(x^2+y^2=1\). Durch den Punkt \(N_2=(-1,0)\) legen wir die Gerade \(y=t(x +1)\). Mit wachsendem \(t\) müsste dann die Parameterkurve von \(N_4=(1,0)\) aus mathematisch positiv durchlaufen werden. \begin{align*} x^2+t^2 (x +1)^2 &=1\\ x^2+t^2x^2+2t^2\;x +t^2&=1\\ (1+t^2)x^2+2t^2\;x&=1-t^2\\ x^2+2\frac{t^2}{1+t^2}&=\frac{1-t^2}{1+t^2} \qquad \text{nun quadratische Ergänzung}\\ \left(x+\frac{t^2}{1+t^2}\right)^2&=\frac{t^4}{(1+t^2)^2}+\frac{(1-t^2)(1+t^2)}{1+t^2} \qquad\text{ 3. bin. Formel und Wurzel}\\ x&=\frac{-t^2}{1+t^2}\pm \frac{1}{1+t^2} \qquad \text{ + ist sinnvoll }\\ x&=\frac{1-t^2}{1+t^2}\\ y&=t\left(\frac{1-t^2}{1+t^2}+1\right)\\ y&=\frac{2t}{1+t^2} \end{align*}

Anregung 5.3 Abschnitt 5.4.3.2 Seite 422		5.3 Erkundung der NURBS für den EK Bauen Sie (z.B. mit GeoGebra) Abb. 5.25 nach und lassen Sie \(C\) wandern. Sie können diese GeoGebra-Datei verwenden. Machen Sie sich klar, dass alle NURBS, die nicht die Stellung \(y(C)=0.5\) realisieren, mathematisch bis ins Unendliche reichen. Wenn Sie Enden sehen, sind das Artefakte. Hinweis Variieren Sie weitere Steuerpunkte. Sie könnten sich auch von diesem Abschnitt 5.4.3.2 anregen lassen, Wege zu einem von Ihnen definierten Ziel zu erfinden.		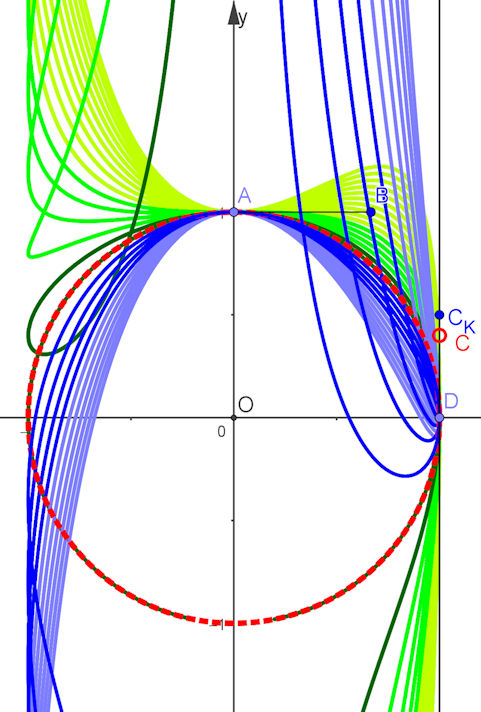Lösung zu 5.3 Kreis als NURBS und seine "Nachbar-NURBS" In diesem Bild ist auf der Senkrechten in \(D\) extra eingetragen der Punkt \(C_K\), der zum Kreisgerüst gehört. Die anderen Gerüstpunkt sind fixiert. Dadurch haben wir gemerkt, dass die oberen NURBS, die grüner werden, \( y(C) \in {0.6, 0.7,\dots, 2}\) erfüllen, die blauen dagegen \( y(C) \in {0.4, 0.3,\dots, -0.5}\). (Leider steht es Buch anders herum.) Immerhin kann man hier - besser als in Abb. 5.26 - erkennen, dass sich der NURBS für \(y(C)=0.4\) schon wieder deutlich nach innen krümmt. In die folgende Formel ist das Gerüst \(A=(0,1),\;B=(\frac{2}{3},1),\;C(1,y(C)),\;D(1,0) \) gleich eingearbeitet. Kurve \( (\frac{1}{1+t^2}(\frac{2}{3} b_1(t)+\frac{4}{3} b_2(t)+2b_3(t))\), \(\frac{1}{1+t^2}(b_0(t)+b_1(t)+y(C)\frac{4}{3} b_2(t)), t,-10,10) \) Kreis als NURBS und Nachbar-NURBS

Anregung 5.4 Abschnitt 5.4.3.3 Seite sss		5.4 Metamorphose der Trisektrix in ihren Konstruktionskreis Die Parameterdarstellung (\(x(t),y(t))\) als NURBS von Gleichung 5.7 (Seite 422 des Buches) für den Einheitskreis kann leicht auf andere Kreise übertragen werden. Einen Kreis \((\bar x(t),\bar y(t))\) mit Radius \(r\) und dem Mittelpunkt \((a,b)\) parametrisiert man nun durch \(\bar{x}(t):=r\, x(t)+a\) und \(\bar{y}(t):=r\, y(t)+b\). Für das Gerüst nimmt man einfach die \(r\)-fache Größe und "heftet" es an einen Kreispunkt an. Aufgabe: Lassen Sie die Trisektrix zu ihrem Konstruktionskreis wandern. Es kann Ihnen jetzt bewusst werden, dass fast die ganze Arbeit schon erledigt ist. Ziel ist nun der Kreis in Abb. 5.26 b) und c), sein Radius ist \(r=2\) und sein Mittelpunkt \((2,0)\). Das oben berechnete Gerüst des Kreises übertragen Sie geometrisch auf den verschobenen und vergrößerten Kreis. Darum brauchen Sie die Kreisgleichung gar nicht. Definieren Sie einen Schieberegler \(s \in [0,1]\) und konstruieren Sie mit dem hier folgenden Hinweis die Punkte \(A',\;B',\;C',\;D'\) auf den Wegen zum Kreisgerüst. Diese setzen Sie als Namen mit \(x(A'),\;\dots \) bzw. \(y(A'),\;\dots \) in Gleichung auf Seite 421 ein. Fertig ist Ihre erste NURBS-Wanderung. Hinweis Wenn ein Punkt \(A\) als \(A'\) gesteuert von einem Parameter \(s\) zum Punkt \(E\) wandern soll, definieren Sie in GeoGebra \(ae=vektor(A,E)\; \; bf=Vektor(B,F) \dots\). Es ist dann \( A'=A+s \;ae\) der gesuchte wandernde Punkt. Anmerkung: In GeoGebra kann man Punkte und Vektoren addieren, man braucht dabei keine "Ortsvektoren" zu definieren. Wenn Sie in dieses Bild klicken, sehen Sie die Animation 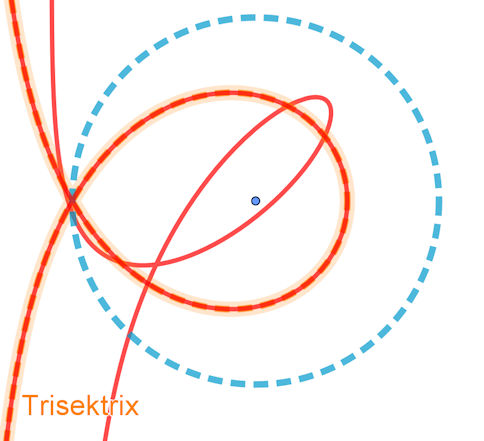Trisektrix animiert		Lösung zu 5.4 Wandlung der Trisektrix in den Kreis, der sie gboren hat. Die geometrische Konstruktion der Trisektrix in in Abb. 5.26 b) gezeigt und in der Legende beschrieben, 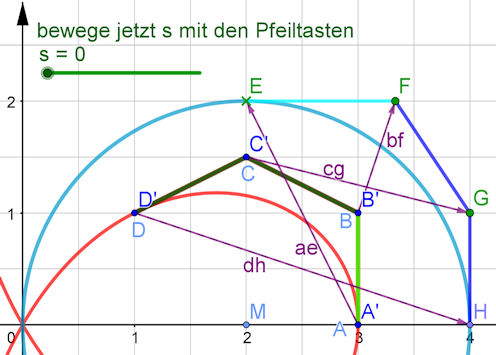Trisektrix Konstruktion Die Schlaufenbreite ist \(3a\) der Mittelpunkt \(M=(2a,0)\) und der Radius ersichtlich \(r=2a\). Da dieser Kreis das Ziel der Metamorphose sein soll, benötigen wir sein Gerüst. Mit \(E=(2a,2a), F=(2a+\frac{2}{3}a,2a), G=(4a,a), H=(4a,0)\) haben wir das Gerüst vom Einheitskreis übertragen. Es ist \(a=1\) in der Zeichnung. Um die Wanderschaft zu organisieren, bei der Punkte vom Gerüst der Trisektrix zu denen des Kreises wandern, eignen sich Vektoren, die gezeichnet mit GeoGebra \(ae=vektor(A,E)\) u.s.w. hier gezeigt sind. Wie auf Seite 421 beschrieben, defnieren wir nun Punkte \(A',B',C',D'\), die auf diesen Vektoren wandern können. Das erreichen wir durch die Definitionen \( A'=A+ s\;ae,\; B'=B+s\;bf, \dots \) mit einem von 0 bis 1 laufenden Parameter \(s\), dabei bedeutet der Abstand \(s\;ae=s \cdot ae\). Im Bild ist noch \(s=0\), darum sieht es so aus, als wäre \(A=A',\;B=B' \dots\) Vorbereitung der Wanderung Nun definieren wir den NURBS, der die Metamorphose leisten soll. Wir nehmen die Formel 5.6 oben auf Seite 421 und lesen Sie in zwei Zeilen. Im Befehl Kurve( < Ausdruck >, < Ausdruck >, < Parameter >, < Anfangswert > , < Endwert > ) sind als Ausdücke \(x(t)\) und \(y(t)\) gemeint. Dabei ist \(A'_x=x(A'), \dots\), denn \(A'\) existiert ja jetzt schon geometrisch, es wird der Name eingetragen. \( \text{Kurve}(1/(1+t^2)\left(x(A')b_0(t)+x(B')b_1(t)+x(C')4/3 b_2(t)+x(D') 2b_3(t)),\\ \text{ ebenso mit y statt x },t,-5,5\right)\) Anmerkung: Der Faktor beim C'-Term erklärt sich so: \(\frac{4}{3} b_2(t)=\frac{4}{3}\cdot 3(1-t)t^2=4 (1-)t^2\). Die \(\frac{4}{3}\) stammen aus der Berechnung der Gewichte auf Seite 420 (Mitte), gelten also nur wegen des Nenners \(1+t^2\) der Parameterdarstellung. 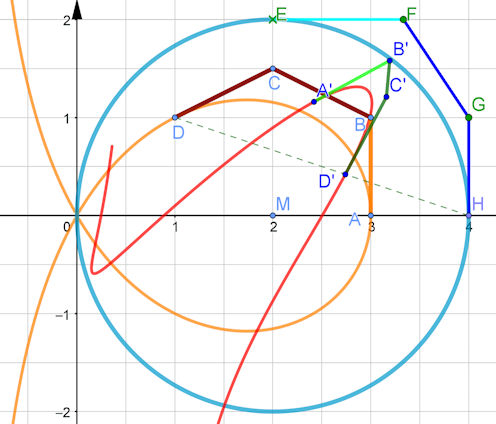Metamorphose der Trisektrix

Dies ist dieWebsite zum Buch: Höhere Mathematik sehen und verstehen START und TIPPS Liste der Zusätze 05 Numerik Anregungen und Lösungen Erstellt: Dez.2020, Update 10. Oktober 2024
Prof. Dr. Dörte Haftendorn	Prof. Dr. Dieter Riebesehl	Dipl.-Math. Dipl.-Ing. Hubert Dammer