Höhere Mathematik sehen und verstehen

Springer Spektrum ISBN 978-3-662-62576-7
ISBN 978-3-662-62577-4 e-book
www.mathematik-sehen-und-verstehen.de
https://masuv.web.leuphana.de 		Dörte Haftendorn

Dieter Riebesehl

Hubert Dammer
>
1.3 Folgen und 1.4 Reihen in 01 Analysis 2D  
1.3 Folgen 1.3.1 Explizit gegebene Folgen
Abschnitt
1.3.1
Seite 12
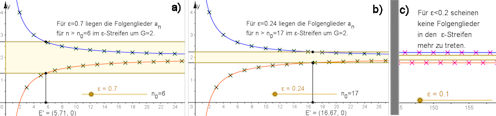 Abb. 1.7 Folgen und Grenzwert. a) und b) beziehen sich auf dieselbe Folge, Bild c) auf eine andere. Ein \(\varepsilon\) kann am Schieberregler frei gewählt werden und es wird dadurch ein \(\varepsilon\)-Streifen um \(y = G\) gelegt, wobei G der vermutete Grenzwert ist. Die beiden Funktionsgraphen zeigen tragende Funktionen einer oberen und einer unteren Teilfolge (Formeln siehe Text). Nun wird, entsprechend der Definition des Grenzwertes für Folgen, angezeigt, ab welchem \(n_0\) die Folgenglieder \(a_n\) in dem
\(\varepsilon\)-Streifen liegen.
Bildteil c) zeigt, dass man so den Grenzwertbegriff verstehen kann, aber keine Gewissheit erlangt. Die hier gezeigte Folge (siehe Text) hat gar keinen Grenzwert, sondern nur zwei Häufungswerte. Ein hinreichend kleiner \(\varepsilon\)-Streifen wird gar nicht mehr betreten.
a) und b) folgen-grenzwert.ggb     c) folgen-grenzwert-c.ggb     gemeinsam im GeoGebra-Book
Zusatz
Abb. 1.7Z1		 Konzept der Cauchy-Folgen:
Eine Cauchfolge \((a_n)\) liegt vor,
wenn es zu jedem \(\varepsilon>0\) eine Zahl \(n_c\in\mathbb N\) gibt,
so dass für alle \(m,\ n >n_c \) stets \(|a_m-a_n|<\varepsilon\) gilt.
  folgen-cauchy-grenzwert.ggb
Das Besondere an dem Konvergenzbegriff von Cauchy ist, dass bei seiner Formulierung der Grenzwert \(G\) gar nicht vorkommt. Stattdessen wird der Ordinaten-Abstand zweier beliebiger Folgenglieder betrachtet. In dem Bildern 1.7Z1 und 1.7Z2 ist o.B.d.A. \(m < n\) realisiert und \(a_m\) ist durch eine rote Raute und \(a_n\) durch einen lila Kreis gezeigt. Die Ordinate von \(a_n\) ist auch an der Stelle \(m\) eingetragen, dadurch gibt die kleine rote Strecke dort das \(|a_m-a_n|\) aus der Definition an. Wie auch bei der Definition zu Abb. 1.7 wird zuerst \(\varepsilon\) gewählt, dann dazu und ein \(n_c\). Rechts davon muss also die Abstandsbedingung erfüllt sein. Ein \(\varepsilon\)-Streifen ist hier gelblich von \(a_m\) aus nach oben gezeichnet und ein grünlicher
\(\varepsilon\)-Streifen nach unten. Dieser \(2 \varepsilon\) breite Streifen ist ab \(n_c\) eingetragen, er verändert seine Höhenlage mit \(a_m\).
Die blaue bzw. die gelbe Funktion sind kleinste obere Schranke bzw. größte untere Schranke. Wenn sie beide in denselben Streifen eintreten, ist \(n_c\) groß genug gewählt.

Ob dann aber wirklich Konvergenz vorliegt, ist nicht sicher, denn es muss ja für jedes \(\varepsilon\) so ein \(n_c\) zu finden sein.
Zusatz
Abb. 1.7Z2
folgen-cauchy-kein-grenzwert.ggb

Genau das geht in Abb. 1.7.Z2 schief. Dort ist das erste Bild noch so wie das zweite von Abb. 1.7.Z1, beide Schranken liegen in demselben \(\varepsilon\)-Streifen. Die violetten Striche deuten schon an, was sich in dem rechten Bild auch zeigt, dass die beiden Schranken nicht dieselbe Asymptote haben. Für hinreichend kleine \(\varepsilon\) gibt es gar keine \(n_c\), von denen an der Abstand beliebiger zweier der Folgenglieder beliebig klein wird.
  Die Betrachtung solcher Bilder kann dem Verständnis dienen, aber grundsätzlich keine Entscheidung zur Konvergenzfrage liefern. Darum gehen wir hier noch auf die Definition der tragenden Funktion ein.
Es ist \( f(x)=(2+(\frac{4}{x}+a)\sin(\frac{2x+1}{2}\pi x)\ \text{mit} \ a_n=f(n)\) und den Schranken \(g(x)=2+a +\frac{4}{x}\) (blau) bzw. \(h(x)=2-a -\frac{4}{x}\)(ocker) und den Asymptoten \(y=2+a \mbox{ bzw. }y=1-a\) (violett).
Dabei lässt \(a\) sich mit einem Schieberegler einstellen. In Abb. 1.7Z1 ist \(a=0\), daher liegt Konvergenz gegen \(G=2\) vor. Sonst ist \(|a_m-a_n|>2a\) für \(n+m\) ungerade. Daher liegt in Abb. 1.7Z2 mit \(a=0.5\) gesichert keine Konvergenz vor.

Beim Aufbau des Zahlensystems werden die rellen Zahlen charakterisiert als die Menge der Grenzwerte aller Cauchyfolgen von rationalen Zahlen. So gewinnt man die neu hinzukommenden Zahlen, ohne sie vorher schon zu kennen. Siehe im Buch Seite 5.
Zusatz Aufgabe

Hier gelöst mit Ti-Nspire. Erklärungsseite für die Behandlung von Folgen mit CAS-TR
Folgen explizit, u.A.    
1.3.2 Rekursiv definierte Folgen
Abschnitt
1.3.2
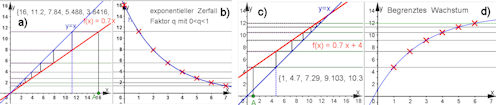
Seite 14		 Abb. 1.8 Rekursion und Iteration.
a) und b) Treppendarstellung für exponentielle Abnahme,
Erklärung im Text zusammen mit der Überleitung zur Zeitdarstellung.
c) und d) entsprechend für begrenztes Wachstum.
folgenrekursiv-zerfall.ggb
folgenrekursiv-begrenzt.ggb
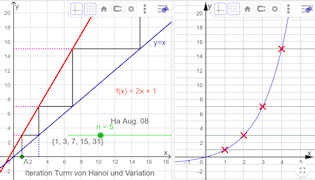
Zusatz   Der Turm von Hanoi
eignet sich sehr als Einstieg in das rekursive Denken.
turmVonHanoi.ggb

Turm von Hanoi rekursiv und explizit+Erläuterung
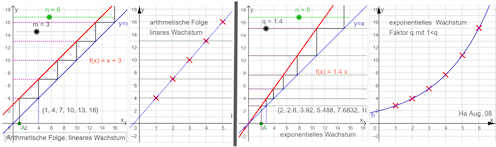
Abschnitt Alle Wachstumsarten systematisch:
Lineares Wachstum
Lineares Wachstum rekursiv und explizit

Exponentielles Wachstum
Exponentielles Wachstum rekursiv und explizit
1.3.3 Folgen von 2D-Punkten und Bildern
Abschnitt
1.3.3.1
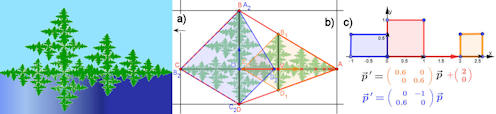
Seite 16		 Abb. 1.9 Der Wald am See.
a) wird durch fraktalen Regen (s.o.) gebildet.
Die Gleichungen in c) enthalten die vollständige Information zum Wald am See, lediglich Himmel und Wasser sind mit Farbfüllung hinzugefügt.
Im Text wird auf b) näher eingegangen.
Wald mit seinen Maßen
Wald am See, Mathematica Quelltext   Dies zum Lesen und Verstehen
Abschnitt
1.3.3.1
Seite 16		 Abb. 1.10 Der Wald am See entsteht mit dem Hutchinson-Operator. Das rote Trapez links wird mit f und g abgebildet. Die entstandenen beiden Trapeze werden ebenso abgebildet, es sind dann vier Trapeze. In diese ist rechts der fraktale Wald aus Abb. 1.9 eingetragen. Weiteres steht im Text.
Abschnitt.
1.3.3.2
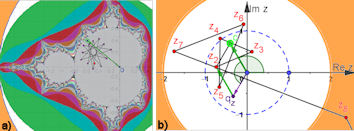
Seite 18		 Abb. 1.11 Mandelbrot-Menge zu \(z_{n+1} = z_n^2+c\)
a) Apfelmännchen, eine vermutlich beschränkte Folge ist eingezeichnet.
b) Die mit GeoGebra ge- rechnete und dargestellte Folge ist mit Sicherheit divergent.
mandel-apfel.ggb
1.4 Reihen 1.4.1 Geometrische Reihe
Abschnitt
1.4.1
Seite 19		 Abb. 1.12 Geometrische Reihen mit
a) und b):\(q=\frac{1}{2},\ a=4\),
c): \(q=\frac{1}{4},\ a=6\)

Beweise für die geometrische Reihe
1.4.2 Harmonische Reihe
Abschnitt.
1.4.2
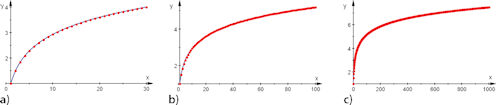
Seite 21		 Abb. 1.13 Harmonische Reihe, Veränderung der Teilsummenfolge.
a), b), c) Teilsummen der harmonischen Reihe mit 30, 100 und 1000 Summanden. Es wird deutlich, dass man durch solche Computerberechnungen keine Klarheit über eine mögliche obere Grenze erlangen kann.
harmonischeReihe-teilsummen.ggb
Abschnitt
1.4.2.1
Seite 21		 Abb. 1.14 Harmonische Reihe.
a) Die Rechtecke haben die Breite 1 und die Höhe \(\frac{1}{n}\).
b) Links von der Stelle \(n\) stehen \((n-1)\) Rechtecke, ihre Flächensumme ist \(s_{n-1}\) und ganz sicher größer als das Integral über die rote Kehrwertfunktion, \(\int_1^{n}\bigl(\frac{1}{x}\bigr)\,d x=\ln n\).
Da der natürliche Logarithmus gegen Unendlich strebt, nimmt er die harmonische Reihe mit ins Unendliche.
harmonischeReihe.ggb
1.4.3 Berühmte Reihen
Abschnitt
1.4.3
Seite 22f		 Berühmte Reihen
(1.1) alternierende harmonische Reihe
Konvergenz wird wie Abb. 1.15 und Abb. 1.16 gezeigt
(1.2) Leibniz-Reihe, sie ist alternierend.
Konvergenz ist in Abb. 1.15 visualisiert
(1.3) Basler Problem, gelöst von Leonhard Euler
(1.4) Eulersche Zahl e, ergibt sich aus der Taylorreihe
Zusatz Abb. zur
Tabelle
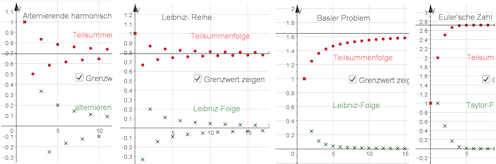
der Reihen 		Abb. zu den berühmten Reihen,
(1.1) Alternierende harmonische Reihe     alternHarmon.ggb
(1.2) Leibniz-Reihe     leibnizReihe.ggb
(1.2) Basler Problem     BaslerProblem.gbb
(1.4) Taylorreihe Reihe für die Eulersche Zahl     eulerscheZahl.ggb
1.4.4 Konvergenz und Umordnung von Reihen
Abschnitt
1.4.3
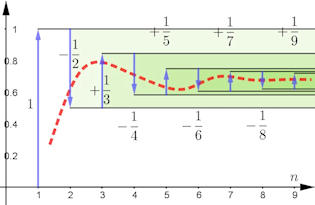
Seite 23		 Abb. 1.15 Konvergenz alternierender Reihen,
gezeigt am Beispiel der alternierenden harmonischen Reihe (1.1)
\(\ln2 = \sum_{n=1}^\infty (-1)^{n+1}\frac{1}{n}\).

Die gestrichelte rote Linie zeigt bildlich an, wo sich der Reihenwert noch aufhalten kann, denn er muss zwischen den waagerechten Strahlen und damit im zunehmend dunkler grün werdenden Bereich liegen.

, denn alternierendeReihe.ggb reagiert empfindlich auf Größenänderung.

Abschnitt
1.4.4
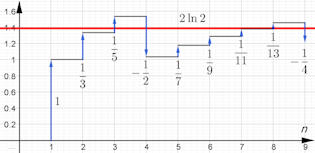
Seite 25		 Abb. 1.16 Alternierende harmonische Reihe umgeordnet. Sie ist nicht absolut konvergent, denn die harmonische Reihe (nur +) divergiert s.o. Abb. 1.14.
Die rote Linie liegt bei \(2ln2\), dem Doppelten des eigentlichen Grenzwertes. Nach dem Riemann'schen Umordnungssatz, kann man jeden Wert, also auch diesen als Grenzwert erreichen. Das geht so:
Man nähert sich dieser Linie an, indem jeweils das nächste positive Glied der Reihe genommen wird, wenn man unterhalb der roten Linie ist, bzw. das nächste negative Glied, wenn man oberhalb ist.
In der folgenen ggb-Datei können Sie auch einen anderen Grenzwert vorgeben und sich das Umordnen zeigen lassen.
ReihenUmordnenInteraktiv.ggb
Reihen umordnen, Mathematica Quelltext     Dies zum Lesen und Verstehen
1.5 Darstellungsvielfalt und Funktionstypen haben eine eigene Leitseite
Website zum Buch: Höhere Mathematik sehen und verstehen 01 Analysis 2D   START und TIPPS     Liste der Zusätze Erstellt: Dez.2020, Update 29. Juli 2021
 Prof. Dr. Dörte Haftendorn  Prof. Dr. Dieter Riebesehl  Dipl.-Math., Dipl.-Ing. Hubert Dammer