Höhere Mathematik sehen und verstehen

Springer Spektrum ISBN 978-3-662-62576-7
ISBN 978-3-662-62577-4 e-book
www.mathematik-sehen-und-verstehen.de
https://masuv.web.leuphana.de 		Dörte Haftendorn

Dieter Riebesehl

Hubert Dammer
1.8 Integralrechnung in 01 Analysis 2D  
1.8.1 Riemannsche Ober- und Untersummen
Abschnitt
1.8.1
Seite 70
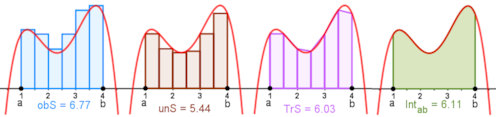
Abb. 1.44 Integral und Riemann’sche Summen.
Obersummen in Blau wählen die maximale Ordinate im Teilintervall,
Untersummen in Braun die minimale Ordinate,
Trapezsummen in Violett sind eigentlich keine Riemann’schen Summen, verbessern aber die numerische Näherung, Sie sind auch die Mittelwerte aus Unter- und Obersummen,
bei Erhöhung der Balkenanzahl streben alle gegen das Integral, die grüne Fläche.
intdef.ggb
int-einf-parabel-rechts.ggb, Einführung bei Parabel
1.8.2 Hauptsatz der Differential- und Integralrechnung
Abschnitt
1.8.2.1
Seite 72
Abb. 1.45 Teppichabrollen - Integralfunktion. a) und c) Ein auf eine Stange gewickelter Teppich mit einer Funktion als oberem Rand wird von \(A\) an bis \(B=(x,0)\) abgerollt. In c) ist mit der roten Kurve gezeigt, welche Teppichfläche an jeder Stelle \(x\) zu sehen war. b) und d) Auch wenn die Randkurve sinkt, wächst die sichtbare Teppichfläche weiter, solange die Randkurve positiv ist.
Die Funktion, die die abgerollte Teppichfläche angibt, hat den Namen Integralfunktion, siehe unten. teppichabrollen.ggb
Abschnitt
1.8.2.2
Seite 72
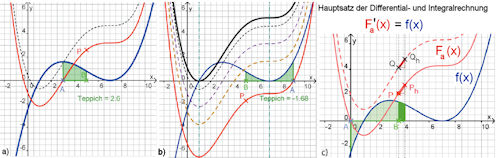
Abb. 1.46 Hauptsatz der Differential- und Integralrechnung. a) und b) zeigen Integralfunktionen zu der (blauen) Funktion \(f\), wie im Text beschrieben. c) Zeigt, dass der Flächenzuwachs beim Ziehen von \(B=(x,0)\) auf \((x+h,0)\) für alle Integralfunktionen gleich ist, denn er hängt offensichtlich von der Stellung von \(A\) gar nicht ab. Denkt man diesen Zuwachs infinitesimal, heißt das, dass alle Integralfunktionen an einer gegebenen Stelle \(x\) dieselbe Zuwachsrate, also dieselbe Steigung haben und dass diese Steigung von der Ordinate \(f(x)\) angegeben wird.
1.) zu a) und c) teppichzuwachs+Stammfkt.ggb
2.) c) allein teppichzuwachs-pur.ggb
  3.) b) und CAS teppich-integralfkt.ggb     Anmerkung: In dieser Datei werden Integralfunktionen mit GeoGebra-CAS bestimmt. Es wird deutlich, dass nicht alle Stammfunktionen von f als Integralfunktionen auftreten können, aber alle Integralfunktionen sind auch Stammfunktionen. Auch die in Abb. c) für den Zuwachs gezeichnete Stammfunktion tritt bei den Integralfunktionen nicht auf. Sie ist der Deutlichkeit halber gewählt.
1.8.3 Wichtige Eigenschaften des bestimmten Integrals
Abschnitt
1.8.3.1
Seite 75
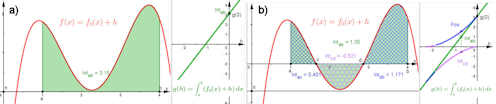
Abb. 1.47 Das Integral als Flächenbilanz. a) Für \(h=0\), also \(f(x) = f_0(x)\ge 0\) ist das Integral die Fläche (grün) unter \(f\) bis zur x-Achse. Rechts in a) ist gezeigt, dass bei gleichmäßiger Verringerung der Verschiebung \(h\) der Integralwert linear sinkt (grüne Gerade). b) Zeigt eine Stellung von \(h\) mit sowohl positiven als auch negativen Werten von \(f\), das Integral ist eine Flächenbilanz. Rechts sind der positive (blau) und der negative Anteil (violett) des Integrals in Abhängigkeit von \(h\) dargestellt. Die Bilanz (grün) aber ändert sich wieder linear.
int-flaeche.ggb
int-fl-bilanz.ggb
Abschnitt
1.8.3.2
Seite 75
Abb. 1.48 Das Integral und Zerlegungen des Integrationsintervalls. a) setzt die Bewegung aus Abb. 1.47 fort. Dabei zeigt sich, dass die Festsetzung \(\int_d^b{f(x){\rm d} x=0}\) für \(d=b\) sinnvoll ist. Bei weiterem Absinken von \(h\) würde das Integral wieder die Flächenbedeutung, aber negativ, erhalten. b) zeigt das Zerlegungsgesetz: es ist dargestellt, dass es unabhängig von der Lage von \(c\) gilt, vorausgesetzt, das Integral über das jeweilige Gesamtintervall existiert.
  a) int-fl-bilanz.ggb (Datei wie für Abb. 1.47 b))
b) int-zerlegung.ggb     Beachten Sie, dass die Kennzeichnung negativ abhängig von der Stellung von c genau richtig erscheint. Siehe GeoGebra->Bedingungen
Abschnitt
1.8.3.3
Seite 76
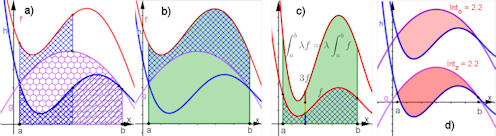
Abb. 1.49 Integral-Gesetze.
a) \(f=g+h\), die blau karierte Integralfläche unter \(h\) wird über \(g\) versetzt "gemalt".
b) Die Integralfläche von \(f\), der Summe, ist dann die Summe der Flächen zu \(g\) und \(h\).
c) Die Integralfläche von \((3 f)\) (grün) ist das 3-fache der Integralfläche von \(f\) (blau kariert).
d) Haben \(f\) und \(g\) höchstens an den Intervallgrenzen gemeinsame Ordinaten, dann ist der Flächeninhalt zwischen beiden Graphen unabhängig von einer gemeinsamen Verschiebung in y-Richtung und damit auch von der Lage der Graphen relativ zur x-Achse, siehe Satz 1.9.
a) und b) Integral-linear-Summe.ggb
c) und d) Integral-linear-lambda.ggb, Vielfache und Zwischenflächen
1.8.4 Partielle Integration und Substitution
Abschnitt
1.8.4
Seite 77		 Zur partiellen Integration haben wir (noch) keine Bilder. Das hängt auch mit dem nachfolgend beschriebenen Problem des Variablengebrauchs zusammen.
Bei Bildern zur Substitution ist es ein grundsätzliches Problem, dass in GeoGebra die freie Variable stets \(x\) heißen muss, man aber bei Substitutionen in \(g(x)\) einen Termteil \(u(x)\) nennt und dann mit \(x=f(u)\) die Funktion \(f(u)\) einführt. Dadurch wird g statt von \(x\) von \(u\) abhängig, handschriftlich drückt man dies durch \(g(u)\) aus und das bedeutet hier NICHT, wie meist üblich, dass für \(x\) einfach \(u\) geschrieben wird, sondern wir definieren eine neue Funktion \(h(u)=g(f(u)\)
In den folgenden Beispielen sind im rechten Grafikfenster konsequent die Funktionen mit \(u\) geschrieben, obwohl sie in Algebrafenster ausschließlich \(x\) als Argumente haben.
In den Legenden der Beispiele können wir das besser herausarbeiten. Die ersten beiden Beispiele sind rechnerisch im Buch vollständig durchgeführt. Lediglich die Bilder sind nun zusätzlich.
Abschnitt
1.8.4
Seite 79

Abb. S79Z1		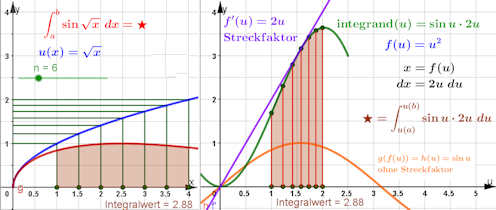 TYP 1: "Ein Termteil wird ersetzt."

Substitution für \( \int_a^b{\sin{\sqrt{x}}\ {\rm d}x} \).
substi-sinwurzelx.ggb

Vorgehensweise: Teil 1: Man entscheidet, welchen Term man substituieren möchte, definiert und zeichnet \(u(x)\). Zu einer äquidistanten Punktfolge zwischen den Grenzen \(a,\ b\) zeichnet man die Folge der Ordinaten der entsprechenden Punkte auf dem Graphen von \(u\) und erhält dadurch eine Punktfolge auf der y-Achse. Diese wird im zweiten Fenster als Folge \(u(a),u(x_1), \dots, u(b)\) eingetragen.

Teil 2: Nun definiert man, i.d.R. nach Umformung, \(x=f(u)\) und bestimmt die Ableitung \(f'(u)\). Im Algebrafenster und für die Zeichnung des violetten Graphen von \(f'\) muss man das Argument \(x\) nennen, aber im CAS kann man wirklich \(u\) nehmen.
Teil 3: Das rechte Grafikfenster braucht nun die, i.d.R. einfachere, Funktion \(h(u)=g(f(u)\), zum Zeichnen wieder mit \(x\) geschrieben. Nun kann man die Punktfolge \((u(x_i),g(u(x_i))\cdot f'(u(x_i))\) bilden und auch den grünen Graphen \({\rm integrand}(u)=h(u)\cdot f'(u)\) bilden und mit Argument \(x\) zeichnen.
Teil 4: Es können jetzt die Intergrationsbefehle verwendet werden: Im linken Fenster für den ursprünglichen Integranden \(g(x)\) (rot) und im rechten Fenster für den in Teil 3 definierten Integranden.
Anmerkung: Die gleichmäßigen Riemann'schen Trapez-Balken links werden rechts transformiert in Riemann'sche Trapez-Balken (annähernd) gleicher Fläche. Der Integralwert, für den den Balkenbreite gegen null strebt, ist daher derselbe.
Den ursprünglichen Integranden \(g(x)\) können Sie beliebig ändern, zum Beispiel substi-coswurzelx.ggb.
Abschnitt
1.8.4
Seite 79

Abb. S79Z2 	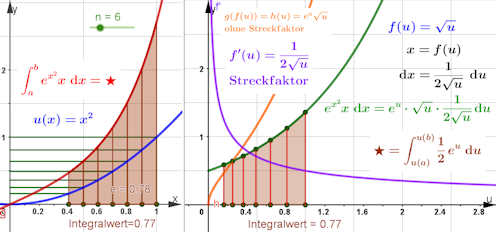	TYP 2: "Die Ableitung erscheint."

Substitution für \( \int_a^b{e^{x^2}x \ {\rm d}x} \).
Wir behandeln diesen Fall mit der Standardmethode, wie sie im vorigen Beispiel durchgeführt ist. Hat man mit der Integrierung durch Substitution Erfahrung, so geht man wie im Buch beschrieben vor und "sieht" x als wesentlichen Bestandteil der Ableitung der naheliegenden Substitution \(u=u(x)=x^2\), was sofort zu \({\rm d}u=2x{\rm d}x\) führt. Man schreibt um: \(\int_a^b {\rm e}^{x^2}x\ {\rm d}x=\) \(\int_{u(a)}^{u(b)}{\rm e}^{u}\frac{1}{2}\ {\rm d}u={\rm e}^x |_{a^2}^{b^2}\).
substi-ex2x.ggb
Abschnitt
1.8.4
Seite 79

Abb. S79Z3 	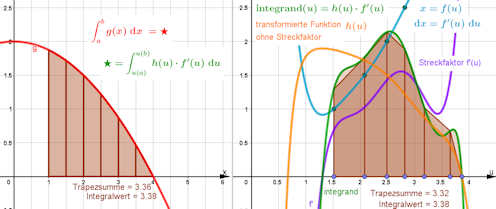	Freier TYP 1: Die Transformation \(x=f(u)\) wird frei gewählt.

Substitution von \(x\) in \( \int_a^b{(2-\frac{x^2}{8})\ {\rm d}x} \) mit einem beliebigen Polynom.
Substitution-freie-Transformation.ggb

Wir wollen auch eine Geogebra-Datei bereitstellen, in der die Substitution nicht fest vorgegeben ist. Die freie Eingabe einer Substitutionsfunktion \(u(x)\) ist aber problematisch, da schwer zu kontrollieren ist, wo das vorgegebene Integrationsinterval "landet" und damit d er Bereich für die Graphik 2 schwer zu bestimmen ist. Deshalb können Sie hier die Funktion \(u(x)\) dadurch festlegen, dass Sie im zweiten Graphikfenster die Funktionswerte \(u(1),\ u(1.5),\ \dots, u(4)\) durch Ziehen der sechs blauen Punkte auf der \(u\)-Achse festlegen. Dann wird \(u(x)\) geeignet interpoliert. Da in Graphik 2 vor allem die Umkehrfunktion \(f(u)\) gebraucht wird, wird diese durch ein (Lagrange-)Polynom interpoliert.
Es ist, wie auch in den anderen Beispielen, \(h(u)=g(f(u))\).
Achten Sie beim Verschieben der Punkte darauf, dass \(u(x)\) monoton wachsend bleibt, sonst gibt es ein unübersichtliches Durcheinander im Bild, obwohl die Rechnung weiterhin funktioniert. Und: ziehen Sie vorsichtig, denn vor allem der Streckfaktor \(f'(u)\) reagiert sehr empfindlich auf die Lage der Punkte!
Die Funktion \(g(x)\) hingegen können Sie gerne ändern.
Abschnitt
1.8.4
Seite 79

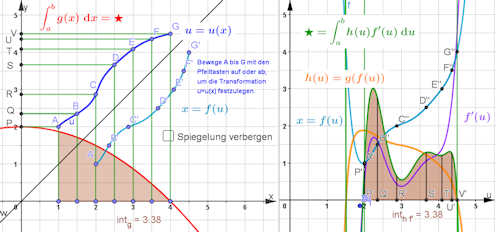
Abb. S79Z4 		Freier TYP 2: Die Substitution \(u=u(x)\) wird frei gewählt.
Um die vorige Transformation besser zu verstehen, wird hier eine Funktion \(u=u(x)\) frei gewählt, die dann auf dieselbe Art, wie in Abb. S79Z1 und S79Z2 zu einer Transformation mit einem Polynom \(x=f(u)\) führt.
Wie schon in der vorigen Legende gesagt, braucht man eine Funktion \(f\), die man ableiten kann.
Darum gehen wir hier folgendermaßen vor:
Die \(u\) definierenden Punkte A bis G können auf einer gleichabständigen Parallelenschar mit den Pfeiltasten (mit feiner Schrittweite von 0.001) beliebig eingestellt werden. \(u\) sollte möglichst monoton werden. Auch ist es schöner, wenn \(u\) wirklich eine Funktion und nicht nur eine Relation wird, siehe unten. Die Funktion \(g(x)\) können Sie auch hier ändern.
substi-frei-vari.ggb
Durch geometrische Spiegelung an der Winkelhalbierenden entstehen die Punkte einer Umkehrrelation, die man durch ein Interpolationspolynom \(f\) verbindet. Eingeschänkt auf den relevanten Bereich spiegelt man diese zurück. Dadurch erhält man \(u\) i.d.R. nicht als Funktion, sondern als Relation, die als Parameterkurve dargestellt wird. Das ändert aber nichts an der Richtigkeit der Substitutionsregel, für die nur \(x = f(u)\) eine Funktion sein muss.
Nun nimmt man die Ordinaten der Punkte A bis G als Abszissen auf der u-Achse im rechten Grafikfenster und geht dann weiter so vor wie bei den obigen Beispielen. Nur im vorigen Beispiel ist - wie hier - \(x=f(u)\) (hellblau) mit den transformierten definierenden Punkten gezeigt.
Man bildet also aus \(f'(u)\) (violett, alle Funktionen in GeoGebra mit x geschrieben) und \(h(u)=g(f(u))\) (orange) ein Produkt (grün) und integriert es.
Es zeigt sich hier, dass für jede Transformation die beiden mit "Stern" gekennzeichneten Integrale übereinstimmen.
1.8.5 + 1.8.6 Flächenfragen, zunächst bei Parameterdarstellung
1.8.7 Flächenfragen bei Polardarstellung
Abschnitt
1.8.7
Seite 81
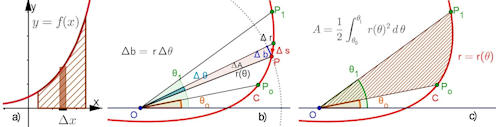
Abb. 1.50 Flächen und Kurven. a) Fläche kartesisch, b) Ansatz für Polarkurven: keilförmiges Flächenstück \(\Delta A\), das bei einer Winkeländerung \(\Delta \theta\) entsteht. c) Die Fläche bei Polarkurven ist ein Kurvensektor.

Abschnitt
1.8.7
Seite 82
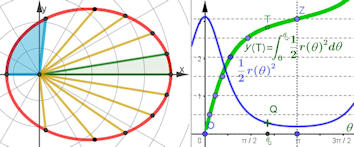
Abb. 1.51 1. und 2. Kepler'sches Gesetz. Das Integral für die Sektoren der Polarkurve \[ r(\theta)=\frac{p}{1-\varepsilon\cos\theta} \] erweist sich als sperrig. Der interaktive Weg zur Integration wird im Text, aber auch im nächsten Zusatz erklärt.
planeten-ellipsen-kepler.ggb
Zusatz Sie sehen in diesem Bild die sogenannte "polar-kartesische Darstellung". Sie ist in diesem Webverbund häufig genutzt, insbesondere hier in www.kurven erkunden und verstehen erklärt.
Die Polargleichung \(r=r(\theta)\) wird als \(r=r(x)\) im 2. Grafikfenster kartesisch dargestellt. Ein Punkt \(K=(x,r(x))\) rechts kann dann als \(K=(r(\theta);\theta)\) im linken Grafikfenster ohne weitere Umrechnungen erscheinen. (In der *.ggb anwählbar.) Hier also wird das Integral \( y(T):=\int_0^t{\frac{1}{2}r(x)\ dx}\) kartesisch auf numerischem Weg berechnet und als Punkt \(T=(t,y(T))\) angezeigt. Da der bewegliche Punkt \(Q\) auf dem Integranden (blaue Kurve) \(t\) erzeugt, existiert die grüne Ortskurve von \(T \). Punkt \(Z\) an der Stelle \(\pi\) gibt also die halbe Ellipsenfläche an. Rechts ist die Ordinate von \(Z\) in 6 gleiche Teile, die Monate, geteilt. Die waagerechten Geraden schneiden die Ortslinie in Punkten, die als schwarze Punkte auf der Ellipse die Stellung der Erde im Monatsrhythmus zeigen. Die gelben Strecken heißen Fahrstrahlen. So ist das 2. Kepler'sche Gesetz visualisiert: In gleichen Zeiten überstreicht der Fahrstrahl gleiche Flächen.
Im Kurvenbuch finden Sie zu den Keplerschen Gesetzen und speziell zu dem Flächenproblem auch eine Datei mit wahrer Flächenberechnung in GeoGebra-CAS
1.8.8 Bogenlänge bei Funktionen und Parameterdarstellung
Abschnitt
1.8.8
Seite 83
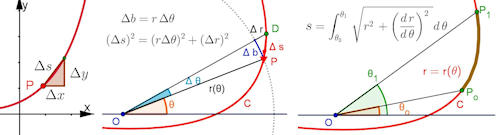
Abb. 1.52 Bogenlänge, links für kartesische Funktionen, dann für Polarkurven, Ansatz und Ausführung.

1.8.9 Bogenlänge von Polarkurven
Abschnitt
1.8.9
Seite 84
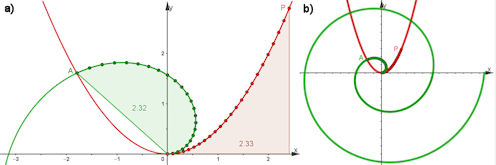
Abb. 1.53 Archimedische Spirale und Parabel. a) zeigt Punkte auf der Spirale und der Parabel \(y=\frac{1}{2}x^2\), die eine gleichlange Kette bilden und auch zu gleichen Flächen führen, siehe Text. In b) ist die Spirale bis \(\theta=4\pi\) dargestellt. Man kann sich vorstellen, dass die Parabel bis zum Punkt \((12.6,\,79),\) den man hier gar nicht mehr darstellen konnte, auf die grüne Spirale aufgewickelt worden ist.
archimedes-bogen+flaeche.ggb

In dieser Datei ist zusätzlich dargestellt: Der Bogen der Parabel von 0 bis \(2\pi\) und der entsprechende Bogen der archmedischen Spirale sind gleich lang. Das Entsprechende gilt auch für Flächen von Pàrabel und Spirale.
1.8.10 Volumen von Rotationskörpern
Abschnitt
1.8.10
Seite 85
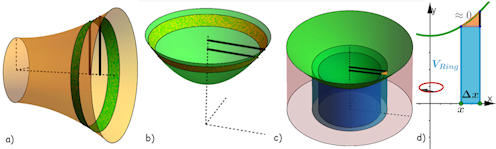
Abb. 1.54 Volumina bei Rotation einer Parabel.
a) Summation von senkrechten Zylinderscheibchen,
b) Summation von waagerechten Zylinderscheibchen,
c) Summation von aufrechten Zylinderringen,
d) halber Querschnitt des Zylinderringes.

1.8.11 Uneigentliche Integrale
Abschnitt
1.8.11.1
Seite 86

In der ggb-Datei sind auch das Bild und die Berechnung des Volumenintegrals mit GeoGebra-CAS. 		Abb. 1.55 Uneigentliches Integral. a) Zur grünen Funktion \(f(x)=\frac{1}{x}\) ist in Rot die bei \(x=1\) beginnende Integralfunktion dargestellt. Die Ordinate bei \(B\) hat also den Wert der braun hinterlegten Fläche, den Wert des Integrals. Im Text wird über das Wachsen des Flächeninhalts nachgedacht, wenn \(B\) gegen Unendlich rückt, dieser wird durch ein uneigentliches Integral berechnet. b) Wenn die in a) gezeigte Fläche um die x-Achse rotiert, entsteht der blaue Trichter, den man sich bis ins Unendliche fortgesetzt denken soll. Es wird sich zeigen, dass sein Volumen endlich ist, obwohl seine Längsschnittfläche, in a) durch Braun und Hellblau angedeutet, unendlichen Flächeninhalt hat.
uneigen-trichter.ggb
Abschnitt
1.8.11.2
Seite 88
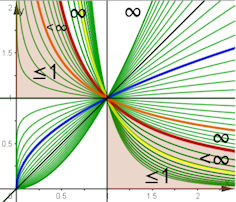
Abb. 1.56 Uneigentliche Integrale der Potenzfunktionen. Die rote Kehrwertfunktion teilt den 1. Quadranten auf in das obere Gebiet, in dem kein uneigentliches Integral über \(x^k\) (grüne Graphen) konvergiert, und das hellbraune, in dem alle konvergieren. Farbig hervorgehoben sind (von rechts oben nach unten) schwarz: \(y=x\), blau: \(y=x^{\frac{1}{2}}=\sqrt{x}\), schwarz: \(y=x^0=1\), orange: \(y=x^{-\frac{1}{2}}= \frac{1}{\sqrt{x}}\), rot: \(y=\frac{1}{x}\), gelb: \(y=\frac{1}{x^2}\). Konvergenz:
\(\qquad I_k=-\frac{1}{k+1}\) für \(k<-1\)
\(\qquad I_a=\frac{1}{a+1}\) für \(-1< a\leq0 \)
uneigentlich-potenzen.ggb
1.9 Anwendungen der Infinitesimalrechnung haben eine eigene Leitseite
Website zum Buch: Höhere Mathematik sehen und verstehen 01 Analysis 2D   START und TIPPS     Liste der Zusätze Erstellt: Dez.2020, Update 29. Juli 2021
 Prof. Dr. Dörte Haftendorn  Prof. Dr. Dieter Riebesehl  Dipl.-Math., Dipl.-Ing. Hubert Dammer