Höhere Mathematik sehen und verstehen
Springer Spektrum ISBN 978-3-662-62576-7ISBN 978-3-662-62577-4 e-book
www.mathematik-sehen-und-verstehen.de
https://masuv.web.leuphana.de
Dieter Riebesehl
Hubert Dammer
|
Höhere Mathematik sehen und verstehenSpringer Spektrum ISBN 978-3-662-62576-7ISBN 978-3-662-62577-4 e-book www.mathematik-sehen-und-verstehen.de
https://masuv.web.leuphana.de
|
Dörte Haftendorn Dieter Riebesehl Hubert Dammer |
|
1.9 Anwendungen der Infinitesimalrechnung in 01 Analysis 2D  |
 1.9.1 Harmonie der rotierten Quadriken |
||
| Abschnitt 1.9.1 Seite 88  |
|
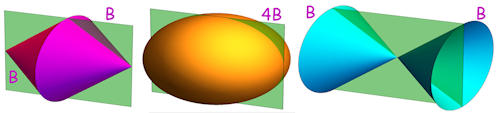
Abb. 1.57 Kegel und Ellipsoid. B ist der Volumen-Baustein \(\frac{1}{3}\pi\,a\,b^2\),
die grüne Fläche hat die Maße \(2a\times 2b\)  |
| Abschnitt 1.9.1 Seite 89 |
|
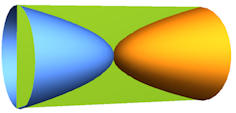
Abb. 1.58 Harmonie, rotierte Parabeln.
Parabeln mit dem Scheitel in O, die auf die
gezeigte Weise in den gedachten Kasten mit
den Seitenlängen (2a,2b,2b) passen, sind bisher
noch nicht dabei, sie „spielen aber auch mit“.
Diese liegenden Parabeln haben die Gleichung \(y^2=\frac{b^2}{a} x. \)
Ergibt sich auch ein Volumen mit B?
 Rotationsparabeln, Mathematica Quelltext
 Dies zum Lesen und Verstehen
|
| Abschnitt 1.9.1.1 Seite 90 |
|
Abb. 1.59 Asymptoten-Kegel und Hyperboloid (bis 2a). B ist der Volumen-Baustein \(\frac{1}{3}\pi\,a\,b^2\).
Das Ellipsoid nimmt zwei Drittel des umfassenden Zylinders ein. Es hat dasselbe Volumen wie das Hyperboloid. Dieses halbiert genau seinen Asymptotenkegel. Ein Ring der Breite d, irgendwo (ab a) aus dem Zwischenraum zwischen Hyperboloid und Asymptoten-Kegel genommen, hat stets dasselbe Volumen wie eine Scheibe der Dicke d aus dem gezeigten Zylinder.
|
| Abschnitt 1.9.1.1 Seite 90 |
|
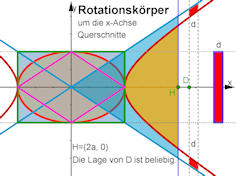
Abb. 1.60 Querschnitte zu den 3D-Abbildungen in diesem Abschnitt. Die verwendeten
Gleichungen sind z.B. \(\frac{x^2}{a^2}\pm\frac{y^2}{b^2}=1\) und \(y=\pm\frac{b}{a}x\).
Für die 3D-Bilder kommt zum \(y^2\)-Term stets ein ebensolcher \(z^2\)-Term hinzu.
Für den Zylinder z.B. anstelle von \(y^2=b^2\) nun \(y^2+z^2=b^2\).
Achten Sie darauf, dass Sie in Abschnitt~1.9.1.1
für "`Volumen zwischen"' nicht über die Differenz der Ordinaten integrieren
dürfen. Parabeln aus Abb. 1.58 sind hier nicht
eingetragen.
Lassen sie sich anregen, eigene Ideen zu verfolgen. 
harmonie.ggb 
|
|
1.9.2 Taylorreihen und Landau-Symbolik |
||
| Abschnitt 1.9.2.1 Seite 94 |
|
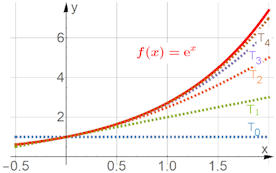
Abb. 1.61 Taylorpolynome
zu \({\rm e}^x\), entwickelt um \(x=0\). Die Taylorpolynome \(T_0(x)\) bis \(T_4(x)\) im
Vergleich mit der Exponentialfunktion selbst (gestrichelt). Die
Variable heißt hier wie üblich \(x\).
TaylorExp.ggb
|
| Abschnitt 1.9.2.1 Seite 95 |
|
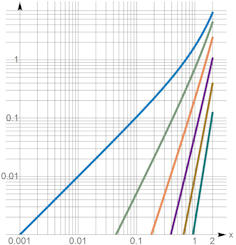
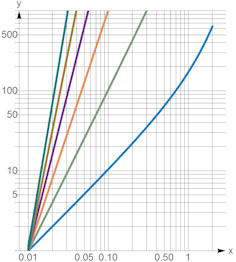
Abb. 1.62 Approximationsgüte zu
\({\rm e}^x\), entwickelt um \(x=0\). Die Differenz zwischen \({\rm e}^x\) und den
Taylorpolynomen \(T_0(x)\) bis \(T_5(x)\) ist hier doppelt-logarithmisch
dargestellt. Näheres zum rechten Bildteil steht im Text, die x-Achse schneidet
hier die y-Achse bei \(y=1\).
TaylorApproximationsGüte, Mathematica Quelltext
Dies zum Lesen und Verstehen
|
 Zusatz zuAbschnitt 1.9.2.1 Seite 93-96 |
Restglieder für Taylorreihen: Nutzen und Problematik Möglicherweise hat die Leserin in unserem Buch im Zusammenhang mit der Taylorapproximation die Erwähnung des Restgliedes \(R_{n+1}\) vermisst. Es besagt, dass die folgende Gleichung gilt: \[ f(x) = T_n(x) + R_{n+1}(x)\quad\text{mit}\quad R_{n+1}(x) = \frac{1}{(n+1)!}f^{(n+1)}(\xi)(x-x_0)^{n+1}. \] Das Restglied sieht aus wie der neue Summand im nächsten Taylorpolynom, allerdings wird die \((n+1)\)-te Ableitung von \(f\) nicht an der Stelle \(x_0\) ausgewertet, sondern an der Stelle \(\xi\). Dabei ist \(\xi\) eine bestimmte Zahl im Intervall \([x_0,x]\), die aber i.A. nicht leicht zu finden ist. Wenn \(f^{(n+1)}\) im genannten Intervall monoton ist, kann man aber \[ T_n(x) + R_{n+1}(x)|_{\xi=x_0} \le f(x) \le T_n(x) + R_{n+1}(x)|_{\xi=x} \] nutzen, um den Funktionswert \(f(x)\) genauer einzugrenzen. Eventuell müssen die Zeichen \(\le\) durch \(\ge\) ersetzt werden, dass hängt davon ab, wie \(f^{(n+1)}\) genau verläuft. Diese Eingrenzung erfordert aber eine weitere Ableitung von \(f\), ist umständlich zu nutzen und schon in manchen einfachen Fällen absolut nutzlos, wie das folgende Beispiel zeigt: Wir wählen \(f(x) = \frac{1}{1-x}\), entwickeln um \(x_0 = 0\), und erhalten \[ T_n(x) = 1 + x + x^2 + x^3 + \dots + x^n,\quad R_{n+1}(x) = \frac{1}{(1-\xi)^{n+1}}x^{n+1}. \] Versuchen wir einmal \(x=0.6=\frac{3}{5}\). Es ist \[ f(0.6) = 2.5,\quad T_n(0.6) = 2.5\cdot(1-0.6^{n+1}),\quad R_{n+1}(x)|_{\xi=0} = 0.6^{n+1},\quad R_{n+1}(x)|_{\xi=0.6} = 2.5\cdot1.5^{n+1}. \] Das letzte Restglied geht aber gegen \(\infty\), wenn der Grad des Taylorpolynoms immer weiter erhöht wird! Z.B. wird für \(n=4\) \[ T_4(0.6) = 2.3056,\quad R_5(x)|_{\xi=0} = 0.0778,\quad R_5(x)|_{\xi=0.6} = 18.9844, \] das ergibt die Eingrenzung \[ 2.3056 + 0.0778 = 2.3834 \le f(0.6) \le 2.3056 + 18.9844 = 21.2900, \] das ist zwar korrekt, aber wenig hilfreich. |
|
| Abschnitt 1.9.2.2 Seite 96 |
|
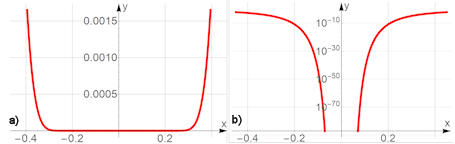
Abb. 1.63 \(f(x)={\rm e}^{^{-\frac{1}{x^2}}}\)
ist nicht analytisch. a) zeigt den Graphen der Funktion in normaler
Darstellung, in b) sind die Funktionswerte logarithmisch abgetragen.
Erst hier wird deutlich, wie schnell und stark die Werte gegen null gehen.
TaylorExp-x(-2), Mathematica Quelltext
Dies zum Lesen und Verstehen
|
| Abschnitt 1.9.2.3 Seite 97 |
|
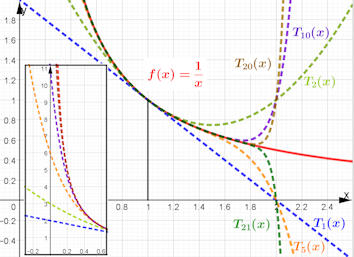
Abb. 1.64 Taylorpolynome zu \(1/x\), entwickelt um \(x=1\).
Die Taylorpolynome \(T_n(x)\) für
\(n=1,2,5,10,20,21\)
(gestrichelt) im Vergleich mit der Funktion selbst.
Nahe \(x=2\) streben die
Taylorpolynome für gerades \(n\) zum
Näherungswert 1, für ungerades \(n\) zum Näherungswert 0, obwohl
\(f(2)=\frac{1}{2}\) ist. Alle
Approximationen sind dort sehr schlecht.
Das links eingefügte kleine Bild zeigt, dass es nahe \(x=0\) nicht
besser ist - aber das kann man in der Nähe einer Polstelle auch nicht
erwarten.
Taylorfuer1durchx.ggb
|
|
1.9.3 Kriterien für Extrema und Wendepunkte |
||
| Abschnitt 1.9.3 Seite 97 |
|
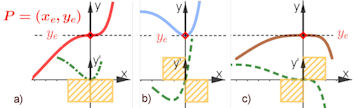
Abb. 1.65 Graphen
von \(f\) und \(f'\) nahe einer möglichen Extremstelle in \(x_e\). Wechselt \(f'\)
bei \(x_e\) das Vorzeichen nicht, dann ist \(f\) mononton.
Wechselt \(f'\) das Vorzeichen bei \(x_e\), dann ist \(x_e\) Extremstelle.
|
| Abschnitt 1.9.3 Seite 100 |
 
|
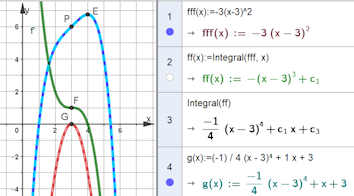
Abb. 1.66 Polynom mit Plattstelle. Es ist
\(f(x)=\frac{1}{4}\bigl(-x^4+12x^3-54x^2+112-69\bigr)\) (blauer Graph).
Die Ableitungen sind: \\
\(f'(x)=\frac{1}{4}\bigl(-4x^3+36x^2-108x+112\bigr)\) (grüner Graph) und \\
\(f''(x)=\frac{1}{4}\bigl(-12x^2+72x-108\bigr)=-3\bigl(x^2-6x+9\bigr)=-3(x-3)^2\)
(roter Graph).
Die Berührung der x-Achse durch \(f''\) in \(G\) garantiert die Krümmung null in
\(f\) und Steigung null in \(f'\). Da \(f''\) in \(G\) aber nicht das
Vorzeichen wechselt, liegt bei \(f'\) kein Extremum, sondern ein Sattelpunkt in
\(F=(3,1)\) vor. Da \(f'\) in \(x=3\) ebenfalls nicht das Vorzeichen
wechselt, hat \(f\) in \(P=(3,6)\) als einzige Besonderheit die Krümmung null.
Dies passt zu Satz 1.19, erst die vierte Ableitung von \(f\) ist
wieder von null verschieden.
plattstelle.ggb
|
| Zusatz |
Zu Abb. 1.66 b): Eine Aufgabe mit einer Plattstelle baut man von unten auf, wie hier mit GeoGebra-CAS gezeigt. Man fängt mit einer Parabel an, die ihren Scheitel auf der x-Achse hat, und integriert sie zweimal. die Integrationskonstanten kann man frei wählen, eine Plattstelle fordert \(c_1\neq 0\). Die entstehenden Funktionen werden von dem CAS gleich im Grafikfenster eingetragen. Daher muss man andere Bezeichnungen wählen. | |
| Abschnitt 1.9.3 Seite 101 |
An \(x_E=\pm k\) und \( x_W=\pm \sqrt{1+k^2}-1 \) sehen wir, dass die Extrema genau für \(k=0\) zusammenfallen, dass aber die Wendepunkte für \(k=0\)
verschieden sind. Der eine fällt mit dem Extremum zusammen. In der Datei sind mit dem CAS diese Terme berechnet worden.
|
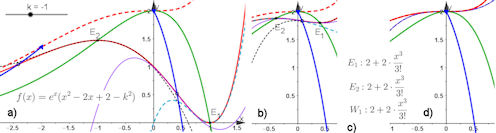
Abb. 1.67 Extrema werden zum
Sattelpunkt. In a) ist eine Funktion (rot) aus einer Funktionenschar
gezeigt, deren zwei Extrema mit wachsendem \(k\) auf der grünen Kurve nach oben
wandern und dabei zusammenrücken, ihre beiden Wendepunkte wandern auf den
blauen Kurven nach oben. Zusätzlich sind dargestellt die
Taylorpolynome dritten Grades, entwickelt für \(E_1,\,E_2\) (dünn gestrichelt)
und den Wendepunkt dazwischen (dünn blau). In b) ist für \(k=-0.4\) der
Graph von \(f\) schon dicht an der rot gestrichelten Grenzlage der Schar, in der
die Extrema zusammenfallen. Die Formeln der Taylorpolynome in c)
zeigen, dass sie für \(k=0\) zusammengefallen sind in eine
Sattelfunktion. In d) ist für \(k=0\) auch \(f\) als Funktion mit
Sattel ohne Extrema zu sehen.
Wenn \(k\) weiter wächst, tauschen \(E_1\) und \(E_2\) ihre Plätze und
wandern ebenso wie die Wendepunkte auf ihren Kurven wieder nach unten.
e-k-ex-sattel.ggb
|
|
1.9.4 Regel von l'Hospital |
||
| Abschnitt 1.9.4 Seite 104 |
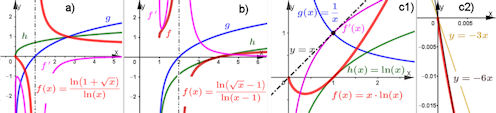
Abb. 1.68 L'Hospital'sche Regel und \(\ln\)-Funktion. In allen Bildern geht es um \(f=\frac{h}{g}\), dabei ist \(h\) stets grün, \(g\) blau und die Quotienten-Funktion rot gezeichnet. Pinkfarben ist jeweils die Ableitung von \(f\) dabei. Im Text des Buches folgen Rechnungen und Untersuchungen. a) \(f(x)=\frac{\ln(\sqrt{x}+1)}{\ln(x)}\), ein Beispiel dafür, dass man das Verhalten für \(x\to \infty\) mit der L'Hospital'schen Regel untersuchen kann, siehe Punkt 3. des Satzes. b) \(f(x)=\frac{\ln(\sqrt{x}-k)}{\ln(x-k^2)}\), ein Beispiel für eine gemeinsame Polstelle in Zähler und Nenner am Rand des Definitionsbereiches und einen besonderen Effekt in der Ableitung. Sie können k variieren.
c) \(f(x)=x\cdot\ln(x)=\frac{\ln(x)}{1/x}\),
ein Beispiel, bei dem ein geschicktes Umwandeln des Typs \(0\cdot\infty\) in den
Typ \(\frac{\infty}{\infty}\) gelingt. Hier wird auch das merkwürdige Verhalten
für \(x\ll 1\) in GeoGebra nachvollzogen.
|
|
| Zusatz |
Zu Abb. 1.68 b) Der erwähnte besondere Effekt in der Ableitung ist zu sehen, wenn \(k\) variiert wird: \(\lim_{x\to k^2}f(x) = 1\), aber dieser Grenzwert scheint mit senkrechter Tangente erreicht zu werden, und zwar "von unten", wenn \(k<\frac{1}{2}\) ist, und "von oben", wenn \(k>\frac{1}{2}\) ist. Das zeigt auch die lila Kurve für \(f'\): sie geht gegen \(\pm\infty\). Was ist für \(k=\frac{1}{2}\)? In diesem Fall hat \(f'\) den Grenzwert 0. Diesen Grenzwert zu finden ist wieder eine schöne Übung mit l'Hospital. Die Ableitung \(f'\) auszurechnen ist etwas mühsam, bietet aber keine besonderen Probleme, man erhält
\[
f'(x) = \frac{k \ln \left(x-k^2\right)+\sqrt{x} \ln \left(x-k^2\right)-2 \sqrt{x} \ln \left(\sqrt{x}-k\right)}{2 \sqrt{x} \left(x-k^2\right) \ln ^2\left(x-k^2\right)}
\]
Setzt man hier \(x=k^2\), so erhält man formal \(f'(k^2) = \frac{\infty-\infty}{0\cdot\infty}\). Das sieht unangenehm aus, da Zähler und Nenner für sich genommen unbestimmte Ausdrücke sind, die nach einer "geschachtelten" Anwendung von l'Hospital zu rufen scheinen. Nach einer kleinen Umstellung, die \(\ln(x-k^2) = \ln(\sqrt x - k) + \ln(\sqrt x + k)\) verwendet, sieht es aber viel besser aus:
\[
f'(x) = \frac{(\sqrt x + k)\ln(\sqrt x + k) - (\sqrt x - k)\ln(\sqrt x - k)}{2 \sqrt{x} \left(x-k^2\right) \ln^2\left(x-k^2\right)}.
\]
Nun nutzt man aus, dass der Logarithmus \(\ln x\) für \(x\to0\) viel langsamer gegen \(-\infty\) geht als jede positive Potenz von \(x\) gegen 0, sodass \(\lim_{x\to0} x^a\ln x = 0\) ist für \(a>0\) (wir geben am Ende dieses Zusatzes eine kurze Begründung dafür). Mit \(x\to k^2\) geht ja \(\sqrt x - k \to0\), damit erhalten wir
\[
\lim_{x\to k^2} f'(x) = \frac{2k\ln(2k)-0}{2k\cdot0} = \pm\infty,
\]
sofern \(\ln(2k)\ne0\) ist. Das Vorzeichen hängt vom Vorzeichen von \(\ln(2k)\) ab: \(+\) für \(2k>1\), \(-\) für \(2k>1\).
Nur der Fall \(2k=1\), also \(k=\frac{1}{2}\) ergibt \(\frac{0}{0}\) und muss mit l'Hospital behandelt werden. Die nötigen Rechnungen, also das Ableiten von Zähler und Nenner, sind mühsam und sollten mit einem guten CAS erledigt werden. Es stellt sich heraus, dass man l'Hospital zweimal anwenden muss, um (mit \(k=\frac{1}{2}\) in \(f\) eingesetzt)
\[
\lim_{x\to\frac{1}{4}}f'(x) = \lim_{x\to\frac{1}{4}}-\frac{1}{\sqrt{x} \left(16 x+12 x \ln ^2\left(x-\frac{1}{4}\right)-3 \ln ^2\left(x-\frac{1}{4}\right)+40 x \ln \left(x-\frac{1}{4}\right)-6 \ln \left(x-\frac{1}{4}\right)\right)} = -\frac{1}{\infty} = 0
\]
zu erhalten. \(f\) hat in diesem Sonderfall also eine waagerechte Tangente am linken Rand des Definitionsbereiches.
Nun noch kurz zur Begründung von \(\lim_{x\to0} x^a\ln x = 0\). Wir führen einige Ersetzungen durch: \(y=x^a,\ x=\sqrt[a]y,\ x^a\ln x = \frac{1}{a}y\ln y\), \(\qquad x\to0 \iff y\to0\): hier wird \(a>0\) gebraucht; \(y=e^{-z},\ z=-\ln y,\ \frac{1}{a}y\ln y = -\frac{1}{a}z\, e^{-z}\), \(\qquad y\to0 \iff z\to\infty\); \(\lim_{z\to\infty} z\, e^{-z} = 0\) wegen des schnellen Wachstums der e-Funktion. |
|
| Abschnitt 1.9.4 Seite 106 |
a)
ahochxdurchx-bhochxdurchx.ggb
b)
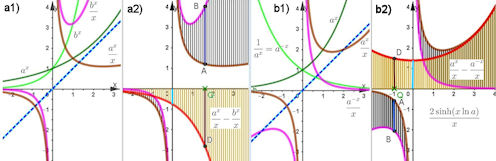
ahochxdurchx-ahoch-minusxdurchx.ggb
|
Abb. 1.69 L'Hospital'sche Regel für \(\infty-\infty\).
a1) und b1) zeigen die Exponentialfunktionen \(a^x\) und \(b^x\) (grün), \(y=x\) (blau) und die Quotienten \(\frac{a^x}{x}\) und \(\frac{b^x}{x}\) (braun bzw. violett) mit ihrem Pol bei \(x=0\), dabei ist in a) \(a=2,\ b=4\), in b) \(a=2,\ b=a^{-1}=\frac{1}{2}\). In a2) und b2) ist die Differenz \(\frac{a^x}{x}-\frac{b^x}{x}\) (braun minus violett) durch schwarze Strecken visualisiert, die jeweils in gleicher Länge gelb von der x-Achse aus dargestellt sind und dadurch an der Differenzfunktion (rot) enden. Speziell: \(\overline{AB}=\overline{QD}\). Die entscheidende Ausnahme ist die Polstelle \(x=0\), an der die stetige Fortsetzung den oben berechneten Wert \(\ln a-\ln b\) (hellblau) hat. In b2) gilt \(\frac{a^x-a^{-x}}{x}=\frac{2\sinh(x\ln a)}{x},\) siehe Text. |
|
1.9.5 Fourierreihen |
||
| Abschnitt 1.9.5 Seite 107 |
|
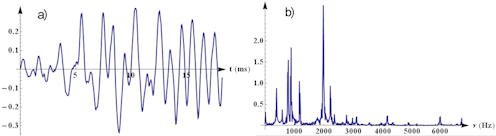
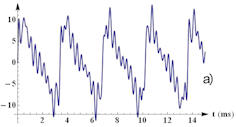
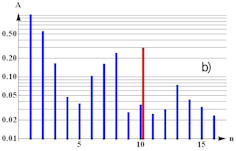
Abb. 1.70 Amplituden und
Spektrum eines Klanges. In a) ist der Luftdruckverlauf eines
Klanges für etwas mehr als 15 ms dargestellt. Gezeigt ist die
Differenz zum Durchschnittswert, der der Stille entspricht.
b) zeigt das Frequenzspektrum dieses Klanges, entnommen aus
ca. 100 ms. Dadurch wird erreicht, dass nur das wesentliche Spektrum,
nicht aber auch das Ausklingen des 1.1 sec langen Klanges zu sehen
ist.
Chordwav, Mathematica Quelltext
Dies zum Lesen und Verstehen
|
| Töne zu
1.71 bzw. 1.73 |
 zu Abb. 1.70 a), zu Abb. 1.70 b)
|
Tonbeispiele:
Links: Der Akkord in chord.wav, aus den Amplituden neu zusammengesetzt. Rechts: Der Akkord in chord.wav, rekonstruiert aus den 6 stärksten Teilfrequenzen im Spektrum. |
| Abschnitt 1.9.5.1 Seite 108 |
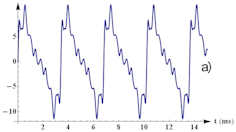
| Abb. 1.71 Amplituden und Spektrum einer Violin-D-Saite. In a) Luftdruckverlauf, b) Fre
quenzspektrum in logarithmischer Darstellung. Die waagerechte Achse ist nicht mit Frequenzen,
sondern mit Obertonnummern bezeichnet.
Abb. 1.72 
|
| Töne zu
1.71 bzw. 1.73 |
zu Abb. 1.71, zu Abb. 1.73
|
Tonbeispiele zum Geigenklang:
zu Abb. 1.71 D-Saite mit 16 Teiltönen zu Abb. 1.73 D-Saite mit 16 Teiltönen mit Störton. Klicken Sie auf die Bilder der Lautsprecher, um die Töne und den Unterschied zu hören. |
| Abschnitt 1.9.5.1 Seite 109 |
 
|
Abb. 1.73 Spektrum einer Violin-D-Saite mit Störung.
a) geänderter Schwingungsverlauf ohne Erkennbarkeit der Störung, b) Spektrum mit Störton, rot hervorgehoben.
|
| Abschnitt 1.9.5.1 Seite 108 |
 |
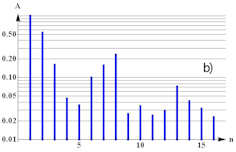
Abb. 1.72 Obertöne einer Violine. a) Schwingungsmodi und zugehörige Obertöne, b)
diese vier Schwingungen in 8 ms, c) Sägezahnschwingung aus 16 Obertönen mit Gibbs’schem
Phänomen, das in Beispiel 1.5 erklärt wird. Die Amplituden sind an Abb. 1.71 angeglichen.
|
| Abschnitt 1.9.5.2 Seite 111 |
|
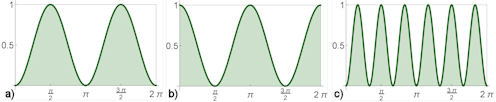
Abb. 1.74 Zur Bestimmung der Normen von
Sinus- und Cosinusfunktionen. In a) ist \(||\sin x||^2\)
als das \(\frac{1}{\pi}\)-fache der Fläche unter dem Integranden dargestellt,
b) und c) zeigen dies für \(||\cos x||^2\) und
\(||\sin k x||^2\).
FourierNorms.ggb
|
| Abschnitt 1.9.5.2 Seite 112 |
|
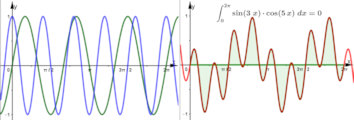
Abb. 1.75 Links sind in Grün und Blau \(\sin 3x\)
und \(\cos 5x\) zu sehen, rechts in Rot ihr Produkt und dessen
Integralfläche. Damit wird gezeigt \(\langle\sin 3x,\cos 5x\rangle=0\).
fourier-sin3cos5.ggb
Es ist in der Datei allgemein \(\sin n x\) und \(\cos m x\) realisiert. So können Sie sich ansehen, dass für jedes \(n\) und jedes \(m\) das Produkt punktsymmetrisch zu \(\pi,0)\) ist und damit -wie im Buch argumentiert- diese beiden Funktionen stets orthogonal sind. |
| Abschnitt 1.9.5.2 Seite 112 |
fourier-sin2sin3.ggb
fourier-cos3cos5.ggb
|
Abb. 1.76 Die
Orthogonalität in den Fällen 2) und 3). a) Beispiel zur
Orthogonalität von \(\sin nx\) (grün) und \(\sin mx\) (blau) für \(n=2\) und \(m=3\)
(Fall 2). Das Produkt (rot) ist zwar nicht mehr punktsymmetrisch zu
\((\pi,0)\), aber im Intervall \([0,\pi]\) wenigstens noch zu \((\frac{\pi}{2},0)\).
Analoges gilt im Intervall \([\pi,2\pi]\). Damit ist die Flächenbilanz null.
b) zu Fall 3), es ist keine Punktsymmetrie mehr auszumachen, hier müssen trigonometrische Formeln helfen: siehe den unmittelbar folgenden Zusatzkasten. Aber auch die beiden Funktionen \(\cos nx\) (grün) und \(\cos mx\) (blau) sind letztlich orthogonal. Siehe Text. |
| Abschnitt 1.9.5.2 S. 113 |
Beweis der trigonometrischen Formel:
\(\cos(a+b)\cos(a-b) = \cos^2 a - \sin^2 b \), die auf Seite 113 benutzt wurde:
Der Einfachheit halber wird das Argument \(x\) weggelassen, die Formeln lauten dann \( \qquad\sin n \sin m = \sin^2 a - \sin^2 b \qquad\) bzw. \(\qquad\cos n \cos m = \cos^2 a - \sin^2 b\). Wegen \(a = \frac{n+m}{2}\) und \(b = \frac{n-m}{2}\) ist \(n = a+b\), \(m = a-b\). Deshalb heißen die Formeln nun \( \qquad\sin(a+b)\sin(a-b) = \sin^2 a - \sin^2 b\ \qquad\) bzw. \( \qquad\cos(a+b)\cos(a-b) = \cos^2 a - \sin^2 b\). Beweis der ersten Formel: Die Additionstheoreme für den Sinus geben
\(\sin(a+b) = \sin a \cos b + \sin b \cos a\), daraus folgt mit der dritten binomischen Formel
\(\sin(a+b)\sin(a-b) = \sin^2 a \cos^2 b - \sin^2 b \cos^2 a = \sin^2 a - \sin^2 a \sin^2 b - \sin^2 b + \sin^2 b \sin^2 a =\sin^2 a - \sin^2 b\).
Beweis der zweiten Formel: Die Additionstheoreme für den Cosinus geben
\(\cos(a+b) = \cos a \cos b - \sin b \sin a\), daraus folgt mit der dritten binomischen Formel \(\cos(a+b)\cos(a-b) = \cos^2 a \cos^2 b - \sin^2 b \sin^2 a = \cos^2 a - \cos^2 a \sin^2 b - \sin^2 b + \sin^2 b \cos^2 a = \cos^2 a - \sin^2 b\). |
|
| Abschnitt 1.9.5.2 Seite 113 |
|
Abb. 1.77 Dreiecksschwingungen.
Hier sieht man Dreiecksschwingungen als denkbare Basis für eine andere Art von
Fourierreihe, von links nach rechts dreieckiger Ersatz für \(\sin x,\
\sin 2x,\ \sin 3x,\ \cos x,\ \cos 2x\).
|
| Abschnitt 1.9.5.2 Seite 115 |
|
Abb. 1.78 Gerade und Ungerade Funktionen. a) Gerade Funktion, b) Ungerade Funktion, c) Teilfunktion periodisch mit Periode \(2\pi\) fortgesetzt als gerade Funktion, d) Teilfunktion periodisch mit Periode \(2\pi\) fortgesetzt als ungerade Funktion. |
| Zusatz |
ungerade-gerade-poly.ggb
Das schwarze Polynom können Sie frei formen. Für das rote Polynom gilt \(k(x)=x^2\cdot p(x)\). Dadurch wird eine waagerechte Tangente beim Schnitt mit der y-Achse erzwungen. Für die gerade Fortzsetzung hätte k nicht den Ursprung erreichen müssen, aber stetige ungerade Fortstetzungen müsssen den Ursprung enthalten. Allerdings müssen diese dort keine waagerechte Tangente haben. |
Freie Polynome rot bzw. schwarz für \(x<=0\) werden rechts auf verschiedene Weise fortgesetzt.
1. Die rot-grüne Funktion ist gerade, stetig und differenzierbar. 2. Die rot-blaue Funktion ist ungerade, stetig und differenzierbar . 3. Die schwarz-gelbe Funktion ist gerade, stetig und NICHT differenzierbar. 4. Die schwarz-violette Funktion ist ungerade, NICHT stetig und damit auch nicht differenzierbar. Sowohl ungerade als auch gerade Funktionen haben mit einer Nullstelle \(x_0\) stets auch \(-x_0\) als Nullstelle. Wenn nämlich \(f(-x)=-f(x)\) gilt, dann auch \(f(-x_0)=-f(x_0)=-0=0\). Gerade Funktionen haben ja zu jedem \((x_a,a)\) stets auch \(( -x_a,a)\) als Kurvenpunkt. In der ggb-Datei ist ein freies Polynom interaktiv formbar. |
| Abschnitt 1.9.5.4 Seite 118 |
|
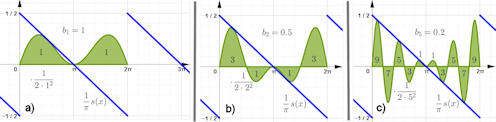
Abb. 1.79 Fourierreihe zum
Sägezahn. Von links nach rechts sind die Integranden für die
Koeffizienten \(b_1,\ b_2\) und \(b_5\) in grün gezeigt, d.h.
\(\frac{1}{\pi} s(x)\sin x,\ \frac{1}{\pi} s(x)\sin 2x,\ \frac{1}{\pi}
s(x)\sin 5x\). Zum Vergleich ist auch \(\frac{1}{\pi} s(x)\) blau
eingezeichnet. Die Zahlen in den grünen Teilflächen geben deren
relative Größe an, die absoluten Werte ergeben sich durch Multiplikation
mit dem extra gezeigten Faktor.
SaegezahnFourier.ggb
|
|
1.9.6 Fouriertransformation |
||
| Abschnitt 1.9.6 Seite 120 |
|
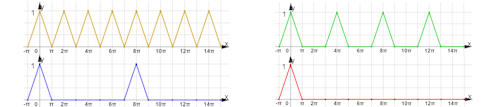
Abb. 1.80 Funktion
fortgesetzt mit verschiedenen Perioden \(T\):
a) \(T =2 \pi\), b) \(T = 4\pi\), c) \(T = 8\pi\),
d) \(T = 16\pi\).
fourierAmplFkt.ggb (als Prototyp).
Siehe auch das Mathematica-Notebook zum nächsten Bild! |
| Abschnitt 1.9.6 Seite 121 |
|
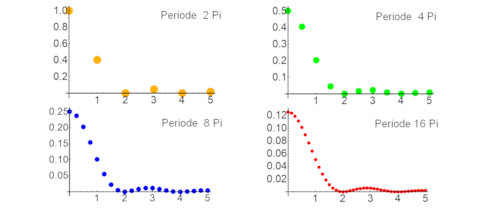
Abb. 1.81 Amplitudenspektren zu verschiedenen Perioden \(T\):
a) \(T = 2\pi\), b) \(T = 4\pi\), c) \(T = 8\pi\), d) \(T = 16\pi\).
FourierSeriesToTransformForTriangle, Mathematica Quelltext
Dies zum Lesen und Verstehen
|
| Abschnitt 1.9.6 Seite 121 |
|
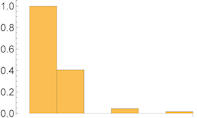
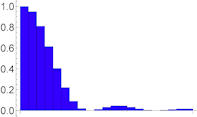
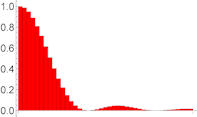
Abb. 1.82 Spektren als
Balkendiagramme für verschiedene Perioden.
a) zu \(2\pi\), b) zu \(4\pi\), c) zu \(8\pi\), d) zu \(16\pi\).
FourierSeriesToTransformForTriangle, Mathematica Quelltext
Dies zum Lesen und Verstehen
|
| Abschnitt 1.9.6 Seite 122 |
|
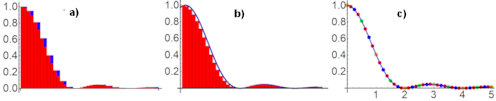
Abb. 1.83 Übergang zur Transformierten:
a) Perioden \(8\pi\) und \(16\pi\) überlagert, b) Periode \(16\pi\) und Transformierte, c) Transformierte mit allen diskreten Spektren.
FourierSeriesToTransformForTriangle, Mathematica Quelltext
Dies zum Lesen und Verstehen
|
|
1.9.7 Laplacetransformation |
||
| Zusatz
Seite 125 |
 |
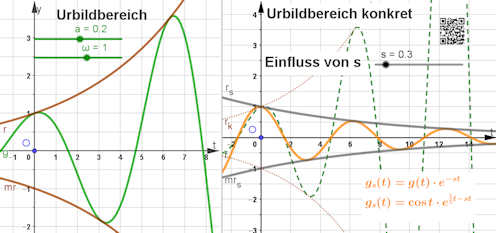Diese Berechungen greifen wir bei den DGLn in
Abschnitt 4.5.7 auf.
Von der Urbildfunktion zum Integranden des Laplace-Integrals. Obwohl links die Funktionsmaxima exponentiell wachsen, i.W. mit \(e^{\frac{1}{5}t}\), drückt der Faktor \(e^{-s\;t}\) für \(s>\frac{1}{5}\) die gegebene Funktion so zusammen, dass das Integral bis \(\infty\) existiert, es ist \[G(s)=\int_0^\infty g(t)e^{-s\;t}{\rm d}t=\int_0^\infty g_s(t){\rm d}t \] die Laplacetransformierte von \(g(t)\), sie ist im nächsten Bildpaar rechts in Rot zu sehen. Laplace-cos-e-plusFuenftel-URs.ggb
|
| Zusatz
Seite 125 |
 |
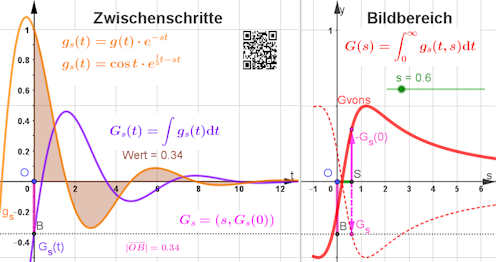Visualisierung des Rechenweges.
Der Integrand \(g_s\) des Laplace-Integrals ist links für \(s=0.6\) in Orange gezeichnet, der Graph hängt stark von \(s\) ab, das können Sie frei in der obigen GeoGebradatei ausprobieren. Zusätzlich ist in Violett eine bestimmte Stammfunktion \(G_s(t)\) zu sehen, für die \(G_s(\infty)=0\) ist. Dann ist der Integralwert \(-G_s(0)\), das ist durch den gespiegelten Vektor von \(\overrightarrow{OB}\) hellviolett zu sehen. Im rechten Bild ist er als Ordinate für \(S=(s,-G_s(0))\) verwendet. Dadurch kann man rechts als rote Ortskurve von \(S\) die Laplacetransformierte erhalten. Weiter ist das Integral in den Grenzen von 0 bis 12 von \(g_s\) als Fläche markiert. Der Integralwert ist Wert=0.34, das ist auch schon \(-G_s(0)\), da bis \(\infty\) nur noch so wenig Fläche hinzukommt. Laplace-cos-e-plusFuenftel-ZB.ggb
|
| Zusatz
Seite 125 |
 |
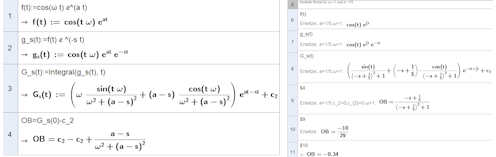Berechung der Laplacetransformierten mit GeoGebra-CAS.
Hierzu ist eine eigene GeoGebra-Datei mit allgemeineren Parametern verwendet worden. Die Zellen werden mit \($1,\;$2,\dots\) angesprochen. \($1\) ist die Urbildfunktion (grün), Achtung: mit \(:=\) definiert, \($2\) ist der Laplace-Integrand (orange). \($3\) ist eine Stammfunktion (violett), das unbestimmte Integral mit Integrationskonstante. In \($4\) sieht man die Laplacetransformierte \(G(s)=\int_0^\infty g_s(t){\rm d}t=G_s(\infty)-G_s(0)=\frac{s-a}{ \omega^2+(s-a)^2}\) Wegen des Minuszeichens steht \(s-a\) anstatt \(a-s\). Laplace-cos-e-CAS.ggb
Laplace-cos-e.nb, Mathematica Quelltext
Dies zum Lesen und Verstehen
|
| Zusatz
Seite 125 |
||
Website
zum Buch: Höhere Mathematik sehen und verstehen
01 Analysis 2D START und TIPPS
 Liste der Zusätze |
Erstellt: Dez.2020, Update |
|
 Prof. Dr. Dörte Haftendorn
| Prof. Dr. Dieter Riebesehl
| Dipl.-Math. Dipl.-Ing. Hubert Dammer
|