Kapitel 4.5+4.6 Knotentheorie Die Neuauflage, die im Herbst 2016 erschienen ist, hat dieses Teilkapitel neu. In der dritten Auflage, die im Frühjahr 2019 erscheinen wird, habe ich einen Abschnitt 4.6 zu keltischen Knoten ergänzt. Dieser zeigt Ihnen, wie Sie mit Hilfe von Gerüstgraphen eigenständig schöne Knoten zeichnen können.

Das Buch "Mathematik sehen und verstehen" wird erfreulicherweise etwa 2019 in der dritten Auflage erscheinen. Diese wird um etwa 20 Seiten umfangreicher sein. Sie befinden sich auf der Website zum Buch: Hier sind die Dateien aus GeoGebra und anderen Mathematik-Programmen, die die Bilder des Buches erzeugt haben. So können Sie alles interaktiv nachvollziehen. Die Vorlesung "Mathematik für alle" ist hier verfügbar. Weiter gibt es Ergänzungen, für die im Buch kein Platz mehr war. Insbesondere sind auch Aufgaben eingefügt. Bei Werkzeuge finden Sie ein Log-Buch und allerlei Hinweise. Falls nach dem Lesen im Buch noch Fragen übrig sind oder Sie Fehler finden, wenden Sie sich gern an mich.

4.5 Theorie der Knoten							4.6 Keltische Knoten			Fort- setzung
4.5.1	4.5.2	4.5.3	4.5.4	4.5.5	4.5.6	4.5.7	4.6.1	4.6.2	4.6.3
Alle Bilder können Sie durch Anklicken in vergrößerter Darstellung in einem neuen Fenster ansehen.

Aufsatz 2014

Diskret verknotet   Kleines Lehrbuch zur Knotentheorie, 26 Seiten Dieser Aufsatz gehört zu einem Vortrag über Knotentheorie, den ich im Herbst 2013 in einem Arbeitskreis der GDM (Gesellschaft für Didaktik der Mathematik) in Saarbrücken gehalten habe. Sie bekommen hier einen Überblick über die spannenden Möglichkeiten der Knotentheorie in "Lernzusammenhängen".

Sorry

An english versiaon of this paper "Knot Theory" is not available yet. You will find informations in the Software KnotPlot of Rob Sharein (Canada) and in Wikipedia.

4.5.1 Definitionen der Knotentheorie
Kap: 4.5.1 nähe von Bild 4.27		Abb. 4.27 Vom Achter-Slip zum mathematischen Knoten und seinem Diagramm.
Kap: 4.5.1 nähe von Bild 4.28		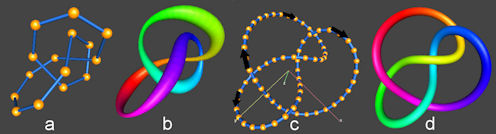Abb. 4.28 Zur Definition mathematischer Knoten als Polygonzüge im Raum.
Kap: 4.5.1 nähe von Bild 4.29	/td>	Abb. 4.29 Erste Knotendiagramme: a) Unknoten, b) Kleeblattknoten, c) Ziffer-Acht-Knoten, d) Studi-Knoten.
Kap: 4.5.1 nähe von Bild 4.30		Abb. 4.30 Es gibt nur drei wirklich verschiedene Knoten mit sechs Kreuzungen. Einer dieser Knoten stimmt mit einem der anderen überein.
4.5.2 Aufgaben und Ziele der Knotentheorie
Kap: 4.5.2 nähe von Bild 4.31	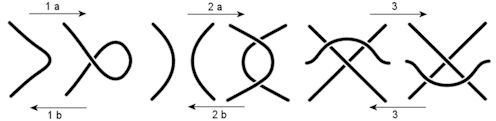Youtube video von N.J. Wildberger über Knotentheorie (englisch) in einer Vorlesung über algebraische Topologie. Teil 2 dieser Vorlesung Knoten und Quantentheorie	Abb. 4.31 Reidemeister-Bewegungen. Mit ihnen kann man ein Knotendiagramm umformen, ohne den gemeinten Knoten zu verändern.
Kap: 4.5.2 nähe von Bild 4.32		Abb. 4.32 Der Perko-Knoten A kann in den Perko-Knoten B übergeführt werden, aus [Knotplot].
4.5.3 Primknoten strukturieren die Knotentheorie
Kap: 4.5.3 nähe von Bild 4.33		Abb. 4.33 Zusammengesetzte Knoten und die Primknoten 4.1 und 5.2
Kap: 4.5.3 nähe von Bild 4.34		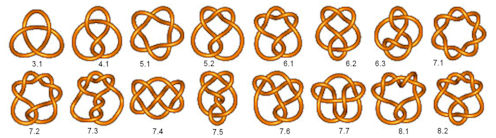Abb. 4.34 Die Liste der ersten Primknoten von 3.1 bis 8.2 Liste der Knoten bis 9.4
4.5.4 Dreifärbbarkeit als Knoteninvariante
Kap: 4.5.3 nähe von Bild 4.35		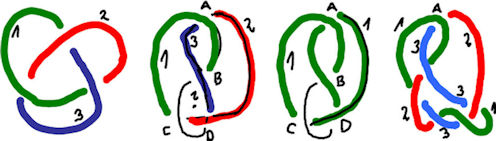Abb. 4.35 Der Kleeblattknoten 3.1 a) und der 6.1-Knoten d) sind dreifärbbar, der Zi.er-Acht-Knoten 4.1 ist nicht dreifärbbar.
Kap: 4.5.3 nähe von Bild 4.36		Abb. 4.36 Der 7.7-Knoten ist dreifärbbar, aber Kreuzung A muss einfarbig sein.
Kap: 4.5.3 nähe von Bild 4.37		Abb. 4.37 Die Dreifärbbarkeit "übersteht" die Reidemeister-Bewegungen.
Kap: 4.5.3 nähe von Bild 4.38		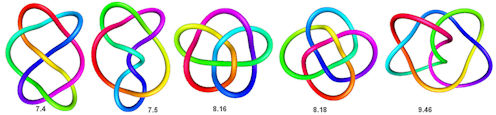Abb. 4.38 Welche dieser Knoten sind dreifärbbar?
4.5.5 p-Etikettierbarkeit als Knoteninvariante
Kap: 4.5.4 nähe von Bild 4.39		Abb. 4.39 Etikettierung mit p = 7 für Knoten 5.2
Kap: 4.5.4	Mathematica-Notebook zu Knotenfarben und p-Etikettierungen dasselbe lesen und verstehen
4.5.6 Alexanderpolynom als Knoteninvariante
Kap: 4.5.5 nähe von Bild 4.40		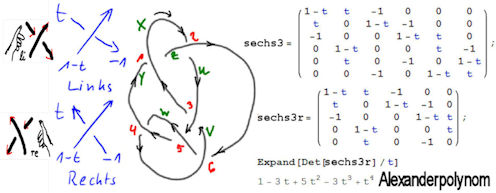Abb. 4.40 Das Alexander-Polynom für den 6.3-Knoten aufstellen.
Kap: 4.5.5	Knotenliste (bis 9.49 ohne 9.13-9.36) mit zugehörigen Alexanderpolynomen 3.1 bis 9.49 und Literaturhinweis Knotentafel 3.1 bis 9.49 bei Knotplot Mathematica-Notebook zu Alexanderpolynomen, aufgenommen in das Notebook zu p-Etikettierungen dasselbe lesen und verstehen Alexanderpolynome mit TI-Nspire   download *tns
4.5.7 Verschlingungen und Zöpfe
Kap: 4.5.6 nähe von Bild 4.41		Abb. 4.41 Verschlingungen: a) Whitehead V. 5.2.1, b) 6.3.3, c) Borromäische Ringe 6.3.2, d) 9.3.16, e) 9.3.13, f) Brunn'sche V. mit 5 Unknoten
Kap: 4.5.7 nähe von Bild 4.42		Abb. 4.42 Vier Schmuckstücke und der Zopf für die Olympischen Ringe (Quelle für c): blacksilvershop)
4.6 Keltische Knoten 4.6.1 Erkunden von Knoten
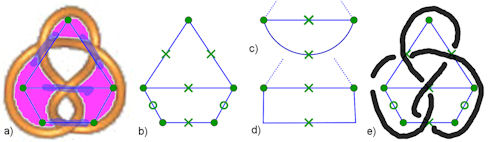
Kap: 4.6.1 nähe von Bild 4.43	b) zeigt einen passenden Gerüst-Graphen, entsprechend Schritt 7 sind Kreuze und Kreise auf den Kanten eingetragen. c) und d) zeigen Alternativen für den unteren Teil, die ohne Zusatz-Kanten auskommen. e) bietet gemäÿ dem Verfahren Von Graphen zum Knoten (siehe unten) das zugehörige Knotendiagramm, das auch für die Alternativen gilt.	Abb. 4.43 a) Vom Knoten zum Graphen, für den Primknoten 4.1 sind Gebiete gefärbt, Brücken angedeutet, Kanten und Ecken eingezeichnet.
Kap: 4.6.1 nähe von Bild 4.44	Abb. 4.44 d) Knoten sein Gerüst-Graph, der Ziffer-Acht-Knoten 4.1 präsentiert in einer von [Tabea Lemke] gezeichneten ansprechenden Gestaltung.
Kap: 4.6.1 nähe von Bild 4.44	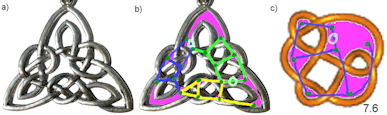Abb. 4.44 a) Ein schottisches Schmuckstück. b) Vom Knoten zum Graphen, Es sind Gebiete gefärbt, Brücken eingetragen, Ecken eingezeichnet, zwei Zusatz-Kanten gekennzeichnet. Drei ähnliche Teile des Knotens sehen wie ein Violinschlüssel aus. Tatsächlich kann man in Blau, Hellgrün und Gelb drei wirkunsgleiche Graphenteile hervorheben. c) zeigt den Primknoten 7.6 und einen passenden Gerüst-Graphen, der diesen Teilen entspricht. Fazit: das schottische Schmuckstück besteht aus drei Exemplaren des Primknotens 7.6 (siehe Abb. 4.34).
4.6.2 Erfinden von Knoten
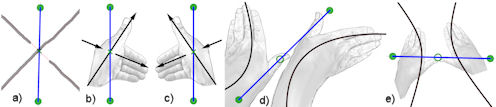
Kap: 4.6.2 nähe von Bild 4.45	d) und e) Mit Kreis versehene Graphenkanten enthalten keine Kreuzung. Entweder verlaufen die Knotenbögen wie in d), der gleich-gerichteten Zweihand-Version, oder wie in e), der gegen-gerichteten Zweihand-Version.	Abb. 4.45 Vom Graphen zum Knoten a), b) und c) Die mit Kreuzen versehenen Graphenkanten werden deutlich von den Knotenbögen geschnitten, Über- oder Unter-kreuzungseigenschaft wird erst im letzten Schritt bestimmt.
Kap: 4.6.2 nähe von Bild 4.46	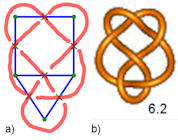Abb. 4.46 Entwickeln eines Knotens aus seinem Gerüst-Graphen: a) Die mit Kreuzen versehenen Graphenkanten werden deutlich von den Knotenbögen mit abwechselnd Über- oder Unterkreuzung geschnitten. b) Es hat sich der Primknoten 6.2 ergeben.
Kap: 4.6.2 nähe von Bild 4.46	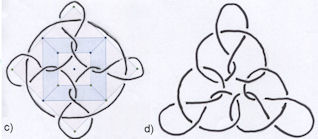Abb. 4.46 Entwickeln eines Knotens aus seinem Gerüst-Graphen: c) Vier Graphen des Primknotens 4.1 aus Abb. 4.43 b) sind im Quadrat angeordnet. Es folgt ein keltischer Knoten, der eine Verschlingung aus Kreis und einem weiteren Unknoten ist. d) Eine Anordnung im Dreieck von Dreien dieser 4.1-Gerüst-Graphen ergibt drei verschlungene 4.1-KnotenT
4.6.3 Ornamente mit keltischen Knoten
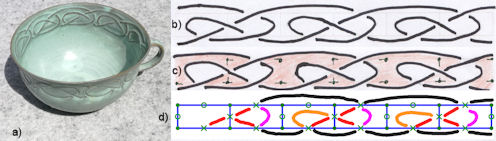
Kap: 4.6.3 nähe von Bild 4.47	b) Abzeichnen des Bandornamentes, c) Färben der Gebiete gemäß Schritt 2, es ergibt sich ein Rechteckband, wenn man in das große Gebiet drei Ecken des Graphen legt. d) zeigt den Gerüst-Graphen. Aber nun ist dort auch gezeigt, wie man von ihm zum Knotenband kommt.	Abb. 4.47 a) Keltisches Bandornament an einer Tasse. [Töpferei Innenton]
Kap: 4.6.3 nähe von Bild 4.48		Abb. 4.48 Ästhetisch ausgeführtes keltisches Bandornament mit dem Gerüst- Graphen, gezeichnet von [Tabea Lemke] .
Kap: 4.6.3 nähe von Bild 4.49		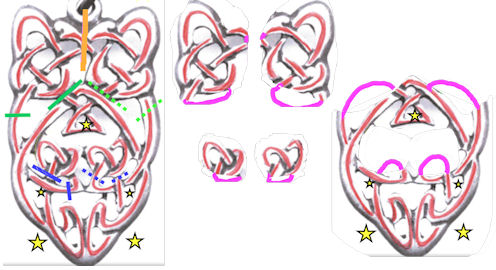Abb. 4.49 Keltischer Schmuckanhänger zerlegt in Primknoten und einen Restknoten. Links sind die Schnitte eingetragen, violett sind dann ist dann die Schließung der offenen Bogenenden gezeigt.

Fortsetzung

Auf meiner Site "www.mathematik-verstehen.de habe ich schon seit 2003 das Thema Knotentheorie. Bitte lesen Sie dort Einführungsseiten für die Lehre und Aufgaben. Direkt zur Knotentheorie

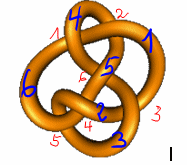Keltischer Stein,    Knoten 6.3,    6.3 mit Bezeichnungen,    Whitehead-Verschlingung

Prof. Dr. Dörte Haftendorn

Erstellt 2014, Update 01.03.2023

www.mathematik-sehen-und-verstehen.de   URL: https://masuv.web.leuphana.de