ISBN 978 662 69291 2 Auflage 2 Book Springer Spektrum
ISBN 978 662 69292 9 Auflage 2 eBook
www.mathematik-sehen-und-verstehen.de
https://masuv.web.leuphana.de (Sicherer Zugang)
Dieter Riebesehl
| Höhere Mathematik sehen und verstehen
ISBN 978 662 69291 2 Auflage 2 Book Springer Spektrum ISBN 978 662 69292 9 Auflage 2 eBook www.mathematik-sehen-und-verstehen.de https://masuv.web.leuphana.de (Sicherer Zugang) |
Dörte Haftendorn Dieter Riebesehl |
| |||||||||||||||||||||||||
| Anregung 2.1 | Aufgaben zur elementaren linearen Algebra | Anregung 2.4 | Approximation durch eine Parabel |
| Anregung 2.2 | Berechnungen zu vier Unterräumen | Anregung 2.5 | Hauptachsentransformation für eine Hyperbel |
| Anregung 2.3 | Basiswechsel | Anregung 2.6 | Hauptachsentransformation für eine Parabel |
| Anregung 2.1
Abschnitt 2.3.4.1 Seite 173 |
2.1 Aufgaben zur elementaren linearen Algebra
1. Eine Matrix \(A\), die \(A\cdot A=A\) erfällt, heißt idempotent, (lat. selbst-mächtig). Die Nullmatrix und die Einheitsmatix sind Beispiele. Suchen Sie eine idempotente \(2{\times} 2\)-Matrix, bei der kein Element null ist. 2. Für zwei Vektoren gelte: \(\|\vec{a}\|=7\) und \(\|\vec{b}\|=4\). Geben Sie den kleinsten und den größten Wert von \(\|\vec{a}-\vec{b}\|\) an. In welchem Intervall liegen die Werte des Skalarproduktes \(\langle \vec{a},\vec{b} \rangle\)? Begründen Sie mit Worten oder Skizzen. 3. \[ A=\left(\begin{smallmatrix}1&1&0\\ 1&0&c\\ 0&1&1 \end{smallmatrix}\right),\quad B=\left(\begin{smallmatrix}1&3&c\\ 1&2&4\\ 1&1&c \end{smallmatrix}\right),\quad C=\left(\begin{smallmatrix}2&1&c\\ 3&3&6\\ c&c&2c \end{smallmatrix}\right) \] Gegeben sind die Matrizen \(A,\; B, \; C\). Für welche Werte von \(c\) ergeben sich jeweils abhängige Spalten oder Zeilen? Versuchen Sie diese ohne lange Rechnungen durch "Hingucken" zu finden. 4. Die Matrix \(A=\left(\begin{smallmatrix}9&c&5\\ c&c&c\\ 3&c&c \end{smallmatrix}\right)\) wird für genau drei Werte von \(c\) singulär, d.h. die Zeilen oder Spalten werden linear abhängig. Geben Sie diese Werte an. Warum kann es nicht mehr als drei geben? 5. Die Matrix \(A=\left(\begin{smallmatrix} u+3&t &u\\ 3&t+u&3t-u\\ 2t+v& 2v&v \end{smallmatrix}\right)\) sieht nicht symmetrisch aus. Berechnen Sie aber \(u, \;t,\;v\) so, dass dann \(A=A^\top\) gilt, sie also symmetrisch wird. 6. Die Matrix \(A=\left(\begin{smallmatrix}a_1+{\rm i}b_1&a_2+{\rm i}b_2\\ a_3+{\rm i}b_3&a_4+{\rm i}b_4 \end{smallmatrix}\right)\) sei echt komplex, d.h. kein Imaginäteil ist null. Wählen Sie die Elemente so, dass \(\det(A) \in \mathbb R\) gilt. Vielleicht können Sie Ihre Lösungsidee etwas verallgemeinern oder (mit CAS) sogar eine allgemeine Lösung finden. |
Lösungen zu 2.1
1. Man findet leicht Beispiele durch Probieren, z.B. \(\left(\begin{smallmatrix}\frac{1}{2}&\frac{1}{2}\\ \frac{1}{2}&\frac{1}{2}\end{smallmatrix}\right)\) oder \(\left(\begin{smallmatrix}2&2\\ -1&-1\end{smallmatrix}\right)\). Mit dem Ansatz \(A=\left(\begin{smallmatrix}a&b\\ c&d\end{smallmatrix}\right)\) kommt man auf die Gleichungen \(a^2 + bc = a,\ ab + bd = b,\ ac + cd = c,\ bc + d^2 = d\) mit der allgemeinen Lösung \( c = \frac{a - a^2}{b},\ d = 1-a \), wie man sofort nachrechnet. (Es gibt noch weitere spezielle Lösungen für \(a=1\) oder \(a=0\), aber die enthalten Nullen als Einträge.) Mit \(a=3,\ b=1\) erhält man z.B. \(A=\left(\begin{smallmatrix}3&1\\ -6&-2\end{smallmatrix}\right)\). Eränzung:Mit Vorgriff auf Abschnitt 2.6.1.3 stellt man fest: Projektionsmatrizen sind automatisch idempotent, da die nochmalige Projektion nichts mehr ändert. Es genügt also, einen Vektor zu finden, der eine Projektionsmatrix erzeugt, die keinen Eintrag \(=0\) enthält. Für unseren Spezialfall erhält man \[ A = \vec v(\vec v^\top\vec v)^{-1}\vec v^\top \] mit \( 0\ne\vec v\in\mathbb R^2\).Aber nicht jede idempotente Matrix ist eine Projektionsmatrix, denn wie man sofort nachrechnet, erhält man mit \( \vec v = (v_1,v_2) \) die Matrixeinträge \( b = c = \frac{v_1v_2}{v_1^2+v_2^2} \), und gerade eben hatten wir ein Beispiel, das nicht symmetrisch ist. Man sieht nun auch, dass wir nur dann keinen Eintrag \(=0\) erhalten, wenn \(v_1\ne0\ne v_2\) ist. 2. Es ist \( 3 \le \|\vec{a}-\vec{b}\| \le 11 \). Den maximalen Betrag erhält man, wenn die Vektoren entgegengesetzt gerichtet sind, den minimalen, wenn sie gleichgerichtet sind. Weiter gilt \( -28 \le \langle \vec{a},\vec{b} \rangle \le 28 \), denn es ist \( \langle \vec{a},\vec{b} \rangle = |\vec{a}\||\vec{b}\|\cos\phi \) mit dem Winkel \(\phi\) zwischen den beiden Vektoren, und der Wertebereich des Cosinus liegt zwischen \(-1\) und 1. 3. \(A\): Mit \( c = -1 \) ist die 3. Spalte gleich der zweiten Spalte minus der ersten. Dies ist die einzige Lösung, denn die Determinante von \(A\) ist linear in \(c\) und wird daher nur für einen Wert gleich null. \(B\): \( c = 4 \), denn dann ist die 3. Spalte das Vierfache der 1. Spalte. Dies ist wieder die einzige Lösung, weil die Determinante linear in \(c\) ist. \(C\): \( c = 0 \), dann ist die dritte Zeile identisch null, oder \( c = 3 \), dann sind 2. und 3. Zeile identisch. Dies sind alle Lösungen, denn die Determinante ist quadratisch in \(c\). 4. Für \(c=0\) sind eine Zeile und eine Spalte identisch null, für \(c=3\) gibt es identische Zeilen und für \(c=5\) identische Spalten. Mehr als drei Werte für \(c\) kann es nicht geben, weil die Determinante höchstens vom Grad 3 in \(c\) ist. 5. Symmetrie erfordert die Gleichheiten \( a_{12}=a_{21},\ a_{13}=a_{31},\ a_{23}=a_{32} \), also \( t=3,\ u=2t+v,\ 3t-u=2v \). \(t\) hat man schon, aus der dritten Gleichung folgt \(u=3t-2v\), durch Gleichsetzen \(6+v=9-2v\), also \(3v=v,\ v=3\), und schließlich \(u=7\) als einzige Möglichkeit mit \[A=\left(\begin{smallmatrix} 10&3&7\\ 3&10&2\\ 7&2&1 \end{smallmatrix}\right)\] als Ergebnis. 6. Man findet sehr leicht Beispiele, das einfachste ist wohl \(A=\left(\begin{smallmatrix} {\bf i}&{\bf i}\\ -{\bf i}&{\bf i} \end{smallmatrix}\right)\). Für die allgemeine Lösung braucht man kein CAS, man schaut sich einfach den Imaginärteil der Determinante an, welchen man zu \( a_1b_4+b_1a_4 - (a_2b_3+a_3b_2) \) errechnet. Für eine reelle Determinante muss dies null ergeben. Man kann z.B. alle Komponenten bis auf \(a_4\) frei wählen und dann \( a_4 = \frac{a_2b_3+a_3b_2-a_1b_4}{b_1} \) setzen. Das geht immer, denn \(b_1\ne0\) war ja vorausgesetzt worden! |
||
| Anregung 2.2
Abschnitt 2.5.1.5 Seite 200 |
2.2 Vier Unterräume im Fall einer \(2\times3\)-Matrix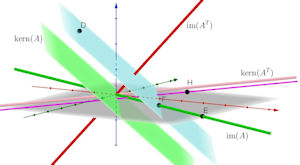
Führen Sie diese Rechnung zu dieser Abb. 2.38 durch. Das Ergebnis ist ja offensichtlich nicht symmetrisch in den Komponenten von \(A\). Ist das in Ordnung so und wenn ja, warum? HinweisDie geometrische Situation ist auch nicht symmetrisch in den Koordinaten! |
Lösung zu 2.2
Ansatz für die Matrix \(A = \bigl(\begin{smallmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23}\end{smallmatrix}\bigr)\), wir setzen \(a_{11}\ne0\) voraus. Weil rang(\(A)=1\) vorausgesetzt ist, ist dann \(a_{22} = \frac{a_{21}}{a_{11}}a_{12},\ a_{23} = \frac{a_{21}}{a_{11}}a_{13}\) usw. Es ist \({\rm kern}(A) = {\rm span}(\left(\begin{smallmatrix} -a_{12} \\ a_{11} \\ 0 \end{smallmatrix}\right), \left(\begin{smallmatrix} -a_{13} \\ 0 \\ a_{11} \end{smallmatrix}\right))\). Sei nun \(D=(x,y,z)\) ein beliebiger Punkt. Die Ebene \(h\) parallel zu \({\rm kern}(A)\) durch \(D\) ist gegeben durch \[ \lambda \left(\begin{smallmatrix} -a_{12} \\ a_{11} \\ 0 \end{smallmatrix}\right) + \kappa \left(\begin{smallmatrix} -a_{13} \\ 0 \\ a_{11} \end{smallmatrix}\right) + \left(\begin{smallmatrix} x \\ y \\ z \end{smallmatrix}\right). \] Die Ebene \(h\) schneidet die xy-Ebene für \(\kappa = -\frac{z}{a_{11}}\). Das Bild von \(A\) in der xy-Ebene ist die von \(\left(\begin{smallmatrix} a_{13} \\ a_{23} \\ 0 \end{smallmatrix}\right)\) erzeugte Ursprungsgerade, ihr Schnitt \(F\) mit \(h\) ist gegeben durch die Gleichungen \begin{align*} -a_{12}\lambda -\frac{z}{a_{11}} + x = \mu\, a_{13}, \\ a_{11}\lambda + y = \mu\, a_{23}, \end{align*} mit einem passenden Faktor \(\mu\). Dies löst man auf, wir brauchen aber nur noch \(\lambda\) und daraus \(F\): \begin{align*} \lambda &= \frac{-a_{11}a_{13}y + a_{11}a_{23}x + a_{13}a_{23}z}{a_{11}^2a_{13} + a_{11}a_{12}a_{23}}, \\ F &= \left(\frac{a_{13} (a_{11} x+a_{12} y+a_{13} z)}{a_{11} a_{13}+a_{12} a_{23}}, \frac{a_{23} (a_{11} x+a_{12} y+a_{13} z)}{a_{11} a_{13}+a_{12} a_{23}},0\right). \end{align*} Das Bild von \(D\) unter \(A\) im \(\mathbb R^3\), genannt \(E\), ist aber offensichtlich \(E = (a_{11} x+a_{12} y+a_{13} z)\left(\begin{smallmatrix} 1 \\ \frac{a_{21}}{a_{11}} \\ 0 \end{smallmatrix}\right)\) = \((a_{11} x+a_{12} y+a_{13} z)\left(\begin{smallmatrix} 1 \\ \frac{a_{23}}{a_{13}} \\ 0 \end{smallmatrix}\right) = F\cdot\frac{a_{11} a_{13}+a_{12} a_{23}}{a_{13}} = (a_{11}+a_{22})F\). Sei \(H = \left(\begin{smallmatrix} x \\ y \\ 0\end{smallmatrix}\right)\) ein beliebiger Punkt in der xy-Ebene, aufgefasst als Urbildpunkt für \(A^\top\), dann ist sein Bildpunkt \(B\) unter \(A^\top\) gegeben als \(B = x\left(\begin{smallmatrix} a_{11} \\ a_{12} \\ a_{13} \end{smallmatrix}\right) + y\left(\begin{smallmatrix} a_{21} \\ a_{22} \\ a_{23} \end{smallmatrix}\right)\). Die Ebene \(e\), die durch \(B\) und die Parallele zu kern\((A^\top)\) durch \(H\) verläuft, hat einen Normalenvektor \(\vec n\), der senkrecht steht auf \(B-H\) und dem Vektor \(\vec k = \left(\begin{smallmatrix} -a_{21} \\ a_{11} \\ 0\end{smallmatrix}\right)\), welcher kern\((A^\top)\) aufspannt. Alle Vektoren senkrecht zu \(\vec k\) haben die Gestalt \(\vec v = \left(\begin{smallmatrix} a_{11} \\ a_{21}\\ C\end{smallmatrix}\right)\), unter diesen müssen wir einen finden, der senkrecht auf \(B-H\) steht, d.h. der Wert von \(C\) muss bestimmt werden. Man rechnet aus: \begin{align*} \vec v\cdot(B-H) = a_{11}(a_{11}-1)x + a_{11}a_{21}y + a_{21}a_{12}x + a_{21}(a_{22}-1)y + a_{13}xC + a_{23}yC = 0 \end{align*} Die Behauptung ist ja, dass \(C\) unabhängig von \(H\), also von \(x\) und \(y\) ist. Die Faktoren an \(x\) bzw. \(y\) sollten also auf dieselbe Gleichung für \(C\) führen. Sie lauten: \begin{align*} \text{für}\ x: \qquad& a_{11}^2 - a_{11} + a_{21}a_{12} + Ca_{13} = 0 \\ \text{für}\ y: \qquad& a_{11}a_{21} + a_{21}a_{22} - a_{21} + Ca_{23}= 0 \end{align*} Wegen \(a_{23}\frac{a_{11}}{a_{21}} = a_{13}\) bietet es sich an, die zweite Gleichung mit \(\frac{a_{11}}{a_{21}}\) zu multiplizieren, man erhält \begin{align*} a_{11}^2 + a_{11}a_{22} - a_{11} + Ca_{13} &= 0, \end{align*} was wegen \(a_{11}a_{22} = a_{21}a_{12}\) (Rang 1!) mit der ersten Gleichung übereinstimmt. Der Normalenvektor ist also wirklich von \(x\) und \(y\) unabhängig und lautet \(\vec v = \left(\begin{smallmatrix} a_{11} \\ a_{21}\\ -\frac{a_{11}^2 + a_{11}a_{22} - a_{11}}{a_{13}}\end{smallmatrix}\right)\). Eine schönere Form bekommt man, wenn man ihn mit \(a_{13}\) multipliziert und nach der Ersetzung \(a_{21}a_{13} = a_{23}a_{11}\) durch \(a_{11}\) dividiert: \begin{align*} \vec n &= \left(\begin{smallmatrix} a_{13} \\ a_{23}\\ -a_{11} - a_{22} + 1\end{smallmatrix}\right). \end{align*} Im Buch ist als Normalenvektor das Negative des eben errechneten Vektors angegeben. Bemerkung: Die Ebene \(e\) ist im Buch nur für den Spezialfall \(H = (0,0,0)\) angegeben worden. Für andere Punkte muss die Gleichung \( e = \{(x,y,z)\ \vert\ (x,y,z)\cdot\vec n = a_{13}x+a_{23}y\} \) heißen. Betrachten wir noch den Fall \(a_{11} = 0\), woraus \(a_{12} = a_{13} = 0\) folgt. Dann können \(a_{21},\ a_{22},\) und \(a_{23}\) nicht alle null sein, sonst wäre der Rang nicht 1. Es ist nicht schwer, die obige Rechnung dann mit nötigen Anpassungen zu wiederholen, und man findet, dass die angegebenen Ergebnisse auch dann korrekt sind. Die Unsymmetrie in den Formeln rührt daher, dass der \(\mathbb R^2\) als Bildraum von \(A\) auf spezielle Weise, nämlich als xy-Ebene, in den \(\mathbb R^3\) eingebettet wurde. Dadurch bekommen die \(z\)-Koordinaten eine Sonderrolle. | ||
| Anregung 2.3
Abschnitt 2.5.1.6. Seite 203 |
2.3 Allgemeiner Basiswechsel Wie sieht ein Basiswechsel für eine allgemeine lineare Abbildung \(A:\mathbb R^n\to\mathbb R^m\) aus, wenn im \(\mathbb R^m\) ebenfalls ein Basiswechsel vorgenommen wird. Stellen Sie sich vor, dass dort die neuen Basisvektoren die Spalten einer Matrix \(S\) bilden. |
Lösungen
Man rechnet \begin{align*} \vec b &= S\vec b', & \vec a &= T\vec b', \\ \vec b &= A\vec a, & S\vec b' &= AT\vec a', \\ \vec b' &= S^{-1}AT\vec a', & \vec b' &= A'\vec a', \\ A' &= S^{-1}AT. \end{align*} | ||
| Anregung 2.4
Abschnitt 2.6.1.4 Seite216 |
2.4 Approximation durch eine Parabel Mit der gleichen Vorgehensweise kann man auch eine approximierende Parabel \(y = ax^2 + bx +c\) zu einer Folge von Punkten finden. Führen Sie das aus. Hinweis: Projizieren Sie \(\vec y\) auf \({\rm span}(\vec 1,\vec x,\vec{x^2})\), wobei \(\vec{x^2} = (x_1^2,x_2^2,\dots,x_n^2)^{\top}\) ist |
Lösungen zu 2.4 Analog zum Fall einer approximierenden Geraden schreibt man \[ \vec{\hat y} = A\left(\begin{smallmatrix} a \\ b \\ c \end{smallmatrix}\right) \quad \text{mit}\quad A = \left(\begin{smallmatrix} 1 & x_1 & x_1^2\\ 1 & x_2 & x_2^2 \\ \vdots & \vdots & \vdots \\ 1 & x_n & x_n^2 \end{smallmatrix}\right). \] Damit bekommt man analog \[ \left(\begin{smallmatrix} a \\ b \\ c \end{smallmatrix}\right) = (A^\top A)^{-1}A^\top\vec y. \] Im folgenden werden Summen der Gestalt \(\sum_{i=1}^n t_i\) mit \(\sum t\) abgekürzt. Damit rechnet man aus \begin{align*} A^\top A &= \left(\begin{smallmatrix} n & \sum x & \sum x^2 \\ \sum x & \sum x^2 & \sum x^3 \\ \sum x^2 & \sum x^3 & \sum x^4 \end{smallmatrix}\right), \\ A^\top\vec y &= \left(\begin{smallmatrix} \sum y \\ \sum (xy) \\ \sum (x^2y) \end{smallmatrix}\right). \end{align*} Das Endergebnis ist \[ \left(\begin{smallmatrix} a \\ b \\ c \end{smallmatrix}\right) = \left(\begin{smallmatrix} n & \sum x & \sum x^2 \\ \sum x & \sum x^2 & \sum x^3 \\ \sum x^2 & \sum x^3 & \sum x^4 \end{smallmatrix}\right)^{-1}\left(\begin{smallmatrix} \sum y \\ \sum (xy) \\ \sum (x^2y) \end{smallmatrix}\right). \] Eine weitere Vereinfachung ist nicht ohne Weiteres möglich. | ||
| Anregung 2.5
Abschnitt 2.7.4.2 Seite 233 |
2.5 Hauptachsentrans- formation für eine Hyperbel 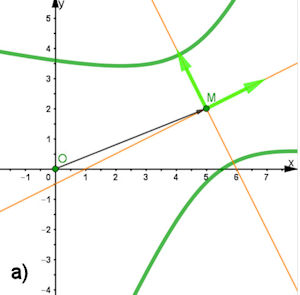 Für die Hyperbel und Abb. 2.52 a) gilt die Gleichung
Für die Hyperbel und Abb. 2.52 a) gilt die Gleichung
\[x^2+4 xy -2 y^2-18x-12y+69=0\] Das Beispiel ist genau parallel zum Vorgehen in Abb. 2.51 entwickelt. Nur haben hier die Eigenwerte verschiedene Vorzeichen. Führen Sie ebenso eine Hauptachsentransformation durch. HinweisSie können sich auch direkt von GeoGebra unterstützen lassen, indem Sie nach Abschnitt 2.7.4.3 vorgehen. |
Lösungen zu 2.5
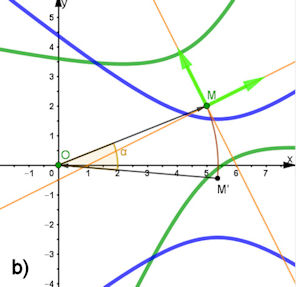 Um die passende Drehmatrix \({\cal T}\)zu finden, müssen wir aus den Termen vom Grad 2, also \(x^2,\,x y,\, y^2,\) die Matrix \(A\) der quadratischen Form aus der Gleichung extrahieren: \(A=\left(\begin{matrix}1&2\\2&-2\end{matrix}\right)\) und deren Eigenwerte bestimmen. \[\left( A-\lambda E\right)
=\left(\begin{matrix}1-\lambda&2\\2&-2-\lambda\end{matrix}\right)\]
\[\left| A-\lambda E\right|=\left|\begin{matrix}1-\lambda&2\\2&-2-\lambda\end{matrix}\right|=
(1-\lambda)(-2-\lambda)-2\cdot2=\lambda^2+\lambda-6
=0 \Longleftrightarrow \lambda=2 \, \vee \, \lambda=-3.\]
Wir berechnen den Eigenvektor zum Eigenwert \(\lambda=2\) aus dem Gleichungssystem
Um die passende Drehmatrix \({\cal T}\)zu finden, müssen wir aus den Termen vom Grad 2, also \(x^2,\,x y,\, y^2,\) die Matrix \(A\) der quadratischen Form aus der Gleichung extrahieren: \(A=\left(\begin{matrix}1&2\\2&-2\end{matrix}\right)\) und deren Eigenwerte bestimmen. \[\left( A-\lambda E\right)
=\left(\begin{matrix}1-\lambda&2\\2&-2-\lambda\end{matrix}\right)\]
\[\left| A-\lambda E\right|=\left|\begin{matrix}1-\lambda&2\\2&-2-\lambda\end{matrix}\right|=
(1-\lambda)(-2-\lambda)-2\cdot2=\lambda^2+\lambda-6
=0 \Longleftrightarrow \lambda=2 \, \vee \, \lambda=-3.\]
Wir berechnen den Eigenvektor zum Eigenwert \(\lambda=2\) aus dem Gleichungssystem
\[\left(\begin{matrix}-1&2\\2&-4\end{matrix}\right)\left(\begin{matrix}v_x\\v_y \end{matrix}\right)=\left(\begin{matrix}0\\0 \end{matrix}\right)\] zu \(v_x=2v_y\), bei Wahl von \(v_y=1\) folgt \(v_x=2\), also \(\vec {v_1}=\left(\begin{matrix}2\\1 \end{matrix}\right)\). Der zweite Eigenvektor muss darauf senkrecht stehen, möglichst in einem Rechtssystem, also \(\vec {v_2}=\left(\begin{matrix}-1\\2 \end{matrix}\right)\). Aus den normierten Eigenvektoren wird die Transformations-Matrix gebildet: \[ {\cal T}= \frac{1}{\sqrt{5}}\left(\begin{matrix}2&-1\\1&2\end{matrix}\right).\] Der erste Summand der quadratischen Form ist damit: \[\vec p \,'\left(\begin{matrix}2&0\\0&-3\end{matrix}\right)\vec p\,'=2 x^2-3y^2.\] Für die linearen Terme der quadratischen Form bestimmen wir: \[2 \vec b^T\, {\cal T}=2\cdot\frac{1}{\sqrt{5}} \left(\begin{matrix}-9&-6 \end{matrix}\right) \left(\begin{matrix}2&-1\\1&2\end{matrix}\right)= \frac{2}{\sqrt{5}}\left(\begin{matrix}-9\cdot 2-6\cdot 1&+9-6\cdot 2 \end{matrix}\right) =\frac{2}{\sqrt{5}}\left(\begin{matrix}-24&-3 \end{matrix}\right). \] Nun können wir die Gleichung der gedrehten Hyperbel aufstellen: \[2x^2-3y^2+\frac{2}{\sqrt{5}}\left(\begin{matrix}-24&-3 \end{matrix}\right) \left(\begin{matrix}x\\y \end{matrix}\right)+69=0\] \[2x^2-3y^2+\frac{2}{\sqrt{5}}\left(-24x -3 y \right)+69=0\] Wir bringen diese Gleichung durch quadratische Ergänzungen in Scheitelform: \[ 2\left(x^2-\frac{1}{\sqrt{5}}\cdot 24 x +\left(\frac{12}{\sqrt 5}\right)^2 -\frac{144}{5}\right) -3\left(y^2+ \frac{2}{\sqrt 5}y++\left(\frac{1}{\sqrt 5}\right)^2 -\frac{1}{5}\right) +69=0. \] Die Scheitelgleichung der blauen Hyperbel nach der Drehung ist: \[2\left(x-\frac{12}{\sqrt{5}}\right)^2 -3 \left(y +\frac{1}{\sqrt{5}}\right)^2=2\frac{144}{5}-\frac{3}{5}-69=57-69=-12.\] Es folgt die Veschiebung des Mittelpunktes \( M'=(\frac{12}{\sqrt 5},\,-\frac{1}{\sqrt 5}) \) in den Ursprung. 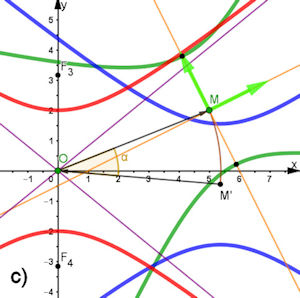 Die rote Hyperbel in liegender Ursprungslage \[2x^2-3y^2=-12\; \Longleftrightarrow \; -\frac{x^2}{6}+\frac{y^2}{4}=1\] hat die Halbachsen \( a=\sqrt 6\) und \(b=2\). HAT-Hyperbel-anreg.ggb | ||
| Anregung 2.6
Abschnitt 2.7.4.2 Seite 234 |
2.6 Hauptachsentrans- formation für eine Parabel 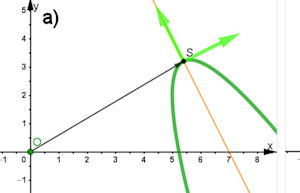 Auch dieses Beispiel ist genau parallel zum Vorgehen in
Abb. 2.51 und Abb. 2.52 entwickelt. Nur ist
hier ein Eigenwert null.
Auch dieses Beispiel ist genau parallel zum Vorgehen in
Abb. 2.51 und Abb. 2.52 entwickelt. Nur ist
hier ein Eigenwert null.
Für die grüne Parabel in Abb. 2.53 gilt die Gleichung: \[4x^2+4x y+ y^2-58 x-24 y+194=0\]. Ihr kann man nicht "ansehen", dass es sich um eine Parabel handelt. HinweisEin DGS wie GeoGebra kann sofort nach Eingabe der ursprünglichen Quadrikgleichung den Mittelpunkt bzw. Scheitel und andere Parameter angeben, beachten Sie Abschnitt 2.7.4.3. |
Lösungen zu 2.6
.jpg) Um die passende Drehmatrix \({\cal T}\)zu finden, müssen wir aus den Termen vom Grad 2, also \(x^2,\,x y,\, y^2,\) die Matrix \(A\) der quadratischen Form aus der Gleichung extrahieren: \(A=\left(\begin{matrix}4&2\\2&1\end{matrix}\right)\) und deren Eigenwerte bestimmen. \[\left( A-\lambda E\right)
=\left(\begin{matrix}4-\lambda&2\\2&1-\lambda\end{matrix}\right)\]
\[\left| A-\lambda E\right|=\left|\begin{matrix}4-\lambda&2\\2&1-\lambda\end{matrix}\right|=
(4-\lambda)(1-\lambda)-2\cdot2=\lambda^2-5\lambda
=0 \Longleftrightarrow \lambda=5 \, \vee \, \lambda=0.\]
Es ist sinnvoll, den Eigenwert \(\lambda=5\) als ersten zu nehmen, da die übliche
Parabelgleichung den Quadratterm \(x^2\) haben soll.
Um die passende Drehmatrix \({\cal T}\)zu finden, müssen wir aus den Termen vom Grad 2, also \(x^2,\,x y,\, y^2,\) die Matrix \(A\) der quadratischen Form aus der Gleichung extrahieren: \(A=\left(\begin{matrix}4&2\\2&1\end{matrix}\right)\) und deren Eigenwerte bestimmen. \[\left( A-\lambda E\right)
=\left(\begin{matrix}4-\lambda&2\\2&1-\lambda\end{matrix}\right)\]
\[\left| A-\lambda E\right|=\left|\begin{matrix}4-\lambda&2\\2&1-\lambda\end{matrix}\right|=
(4-\lambda)(1-\lambda)-2\cdot2=\lambda^2-5\lambda
=0 \Longleftrightarrow \lambda=5 \, \vee \, \lambda=0.\]
Es ist sinnvoll, den Eigenwert \(\lambda=5\) als ersten zu nehmen, da die übliche
Parabelgleichung den Quadratterm \(x^2\) haben soll.Wir berechnen den Eigenvektor zum Eigenwert \(\lambda=5\) aus dem Gleichungssystem \[\left(\begin{matrix}-1&2\\2&-4\end{matrix}\right)\left(\begin{matrix}v_x\\v_y \end{matrix}\right)=\left(\begin{matrix}0\\0 \end{matrix}\right)\] zu \(v_x=2v_y\), bei Wahl von \(v_y=1\) folgt \(v_x=2\), also \(\vec {v_1}=\left(\begin{matrix}2\\1 \end{matrix}\right)\). Der zweite Eigenvektor muss darauf senkrecht stehen, möglichst in einem Rechtssystem, also \(\vec {v_2}=\left(\begin{matrix}-1\\2 \end{matrix}\right)\). Aus den normierten Eigenvektoren wird die Transformations-Matrix gebildet: \[ {\cal T}= \frac{1}{\sqrt{5}}\left(\begin{matrix}2&-1\\1&2\end{matrix}\right).\] Der erste Summand der quadratischen Form ist damit: \[\vec p \,'\left(\begin{matrix}5&0\\0&0\end{matrix}\right)\vec p\,'=5 x^2+0y^2.\] Für die linearen Terme der quadratischen Form bestimmen wir: \[2 \vec b^T\, {\cal T}=2\cdot\frac{1}{\sqrt{5}}\left(\begin{matrix}-29&-12 \end{matrix}\right) \left(\begin{matrix}2&-1\\1&2\end{matrix}\right)= \frac{2}{\sqrt{5}}\left(\begin{matrix}-29\cdot 2-12\cdot 1&+29-12\cdot 2 \end{matrix}\right) =\frac{2}{\sqrt{5}}\left(\begin{matrix}-70&5 \end{matrix}\right). \] Nun können wir die Gleichung der gedrehten Parabel aufstellen: \[5 x^2 +\frac{2}{\sqrt{5}}\left(\begin{matrix}-70&5 \end{matrix}\right)\cdot \left(\begin{matrix}x\\y \end{matrix}\right)+194=0\] \[5 x^2+\frac{2}{\sqrt{5}}\left(-70x+5y\right)+194=0\] Wir bringen diese Gleichung durch eine quadratische Ergänzung in Scheitelform: \[ 5\left(x^2-\frac{2}{\sqrt{5}}\cdot 14 x +\left(\frac{14}{\sqrt 5}\right)^2 -\frac{14^2}{5}\right)+2\sqrt 5 y+194=0. \] Die Scheitelgleichung der blauen Parabel nach der Drehung ist \[y=-\frac{\sqrt{5}}{2} \left( x-\frac{14}{\sqrt{5}}\right)^2+\frac{1}{\sqrt{5}}.\] .jpg) Die rote Parabel zeigt in Ursprungslage nur den Öffnungsfaktor: \[ y=-\frac{\sqrt{5}}{2} x^2.\] HAT-Parabel-anreg.ggb | ||
|
|||||||