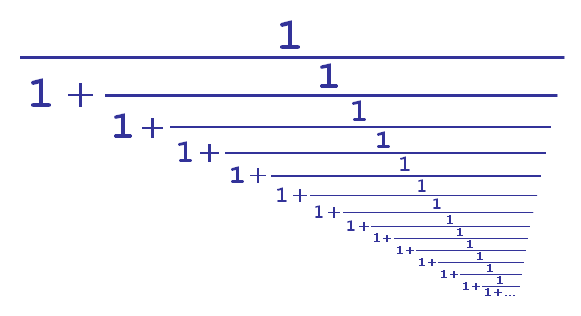
numlib::contfrac(123/1234, 1),
numlib::contfrac(123/1234, 3),
numlib::contfrac(123/1234, 5)
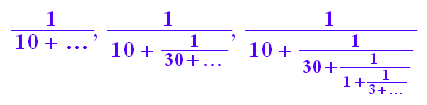
Kettenbrüche
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Juni 09 Update 10.06.09
Web: www.mathematik-verstehen.de http://haftendorn.uni-lueneburg.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Kettenbrüche sind in den CAS meist vorhanden. continued fraction
numlib::contfrac(123/1234, 1),
numlib::contfrac(123/1234, 3),
numlib::contfrac(123/1234, 5)
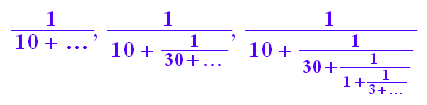
Erst ist die in einen Kettenbruch zu entwickelnde Zahl zu nennen,
dann die Anzahl der Stellen, die man durch den Kettenbruch
annähern will.
z:=PI:
numlib::contfrac(z, 1),
numlib::contfrac(z, 3),
numlib::contfrac(z, 5),
numlib::contfrac(z, 7),
numlib::contfrac(z, 9)
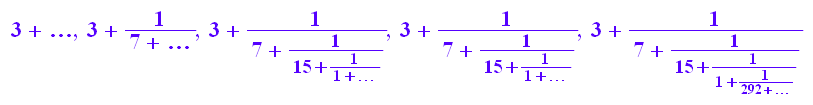
numlib::contfrac(z, 5)
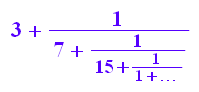
za:=numlib::contfrac(z, 5);
zaf:=numlib::contfrac::rational(za)
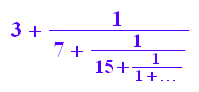

Ein abgebrochener Kettenbruch dient als Näherung, hier für PI
float(zaf);float(PI);
![]()
![]()
Die Millionstelstelle ist schon sicher.
Der kleine Bruch mit 292 signalisiert nur einen kleinen Fehler.
#######################
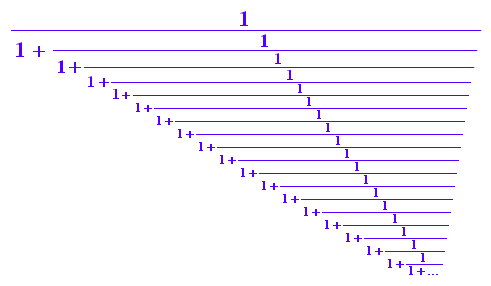
Goldener Schnitt
p:=(sqrt(5)-1)/2
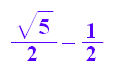
numlib::contfrac(p, 5)
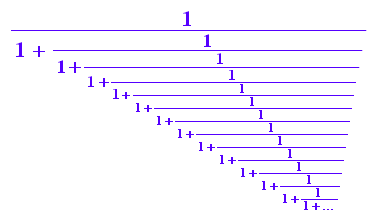
pa:=numlib::contfrac(p, 7);
paf:=numlib::contfrac::rational(pa);
float(paf);float(p);

![]()
![]()
Um 7 stellen richtig zu haben, braucht man schon eine Entwicklung
mit 19 Bruchstrichen.
pa:=numlib::contfrac(p, 5);